Algorithm --> n位数去掉k位后找最小数

去掉K位求取最小数

　　一个n位的数，去掉其中的k位，怎样使留下来的（n-k）位数按原来的前后顺序组成的数最小

例如

8314925去掉4个数，留下125最小，注意有前后顺序要求，要是没有顺序当然是123。

解决方案

贪心算法，在每次被访问的位置保证有最优解。

思路一

分析：求一共n位，求其中的m位组成的数最小。那么这个m位的数，最高位应该在原数的最高位到第m位区间找，要不然就不能当第m位了，如下图（得到3位数最小，要是百位数在25中找，就当不了百位数了）：

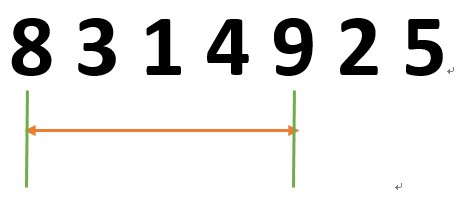
同样找十位数时只能在百味数到目前位置中间搜，整个过程图示如下：

注意

在区间有多个最小值，取距离最大的，保证下一位数有足够大的查找空间。

参考代码

#include <iostream>
#include <cstdlib>
#include <cassert>
using namespace std;
int *q;

int findMinIndex(int arr[], int beg, int end) //[]
{
    if(beg > end)
        return -;
    int minv = arr[beg];
    int minIndex = beg;
    for(int i = beg + ; i <= end; ++i)
    {
        if(arr[i] < minv)
        {
            minv = arr[i];
            minIndex = i;
        }
    }
    return minIndex;
}

int getRemain(int arr[], int size, int k)
{
    assert(size > k && k >= );
    int rev = , revIndex = -;
    for(int i = size - k; i < size; ++i)
    {
        revIndex = findMinIndex(arr, revIndex + , i);
        rev = rev *  + arr[revIndex];
    }
    return rev;
}

int main()
{
    int arr[] = {, , , , , , };
    size_t size = sizeof(arr) / sizeof(int);

    int remainNum;
    for (int k = size-; k > ; --k)
    {
        int remainNum = getRemain(arr, size, size - k);
        cout << "When k = " << k << ", the remaining value is:" << remainNum << endl;
    }

}

结果

分析

时间复杂度O(KN)

思路二

分析：从前往后找，每次访问一位，比较该位前边的数，如果比该位大，果断干掉，例如：

同样以此往后遍历，知道干掉个数为k或访问到最后了，整个过程图示如下图。当然遍历到最后还没有干掉K个元素，说明剩下的已经为升序了，这样就在留下的数中取出前（n-k）个，整合成整数就是最小值。

参考代码

#include <iostream>
#include <cassert>
using namespace std;

int getRemain(int *arr, int size, int k)
{
    assert(size > k && k > );
    int tmp = size - k;
    int cur = , pre;
    int rev = ;
    while(k !=  && cur < size)
    {
        pre = cur - ;
        while(pre >= )
        {
            if(arr[pre] >= arr[cur])
            {
                for(int i = pre; i < size; ++i)
                    arr[i] = arr[i+];
                --cur;
                --k;
                --size;
            }
            --pre;
        }
        ++cur;
    }

    for(int i = ; i < tmp; ++i)
    {
        rev = rev *  + arr[i];
    }
    return rev;
}

int main()
{
    int arr[] = {, , , , , , };
    size_t size = sizeof(arr) / sizeof(int);

    int remainNum;
    remainNum = getRemain(arr, size, );
    cout << "When k = " <<  << ", the remaining value is:" << remainNum << endl;
}

分析

时间复杂度O(KN)