python——对图像进行卷积操作，使用多个滤波器

　　线性滤波可以说是图像处理最基本的方法，它可以允许我们对图像进行处理，产生很多不同的效果。做法很简单。首先，我们有一个二维的滤波器矩阵（有个高大上的名字叫卷积核）和一个要处理的二维图像。然后，对于图像的每一个像素点，计算它的邻域像素和滤波器矩阵的对应元素的乘积，然后加起来，作为该像素位置的值。这样就完成了滤波过程。

　　对图像和滤波矩阵进行逐个元素相乘再求和的操作就相当于将一个二维的函数移动到另一个二维函数的所有位置，这个操作就叫卷积或者协相关。卷积和协相关的差别是，卷积需要先对滤波矩阵进行180的翻转，但如果矩阵是对称的，那么两者就没有什么差别了。

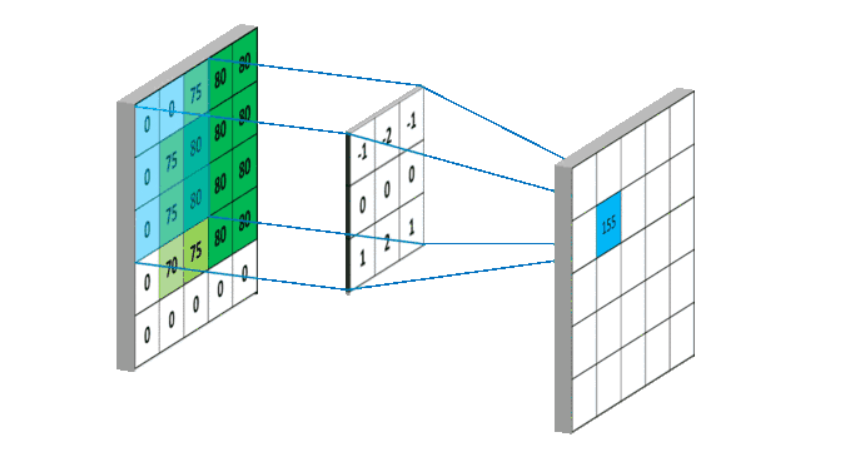
Correlation 和 Convolution可以说是图像处理最基本的操作，但却非常有用。这两个操作有两个非常关键的特点：它们是线性的，而且具有平移不变性shift-invariant。平移不变性指我们在图像的每个位置都执行相同的操作。线性指这个操作是线性的，也就是我们用每个像素的邻域的线性组合来代替这个像素。这两个属性使得这个操作非常简单，因为线性操作是最简单的，然后在所有地方都做同样的操作就更简单了。

实际上，在信号处理领域，卷积有广泛的意义，而且有其严格的数学定义，但在这里不关注这个。

2D卷积需要4个嵌套循环4-double loop，所以它并不快，除非我们使用很小的卷积核。这里一般使用3x3或者5x5。而且，对于滤波器，也有一定的规则要求：

1）滤波器的大小应该是奇数，这样它才有一个中心，例如3x3，5x5或者7x7。有中心了，也有了半径的称呼，例如5x5大小的核的半径就是2。

2）滤波器矩阵所有的元素之和应该要等于1，这是为了保证滤波前后图像的亮度保持不变。当然了，这不是硬性要求了。

3）如果滤波器矩阵所有元素之和大于1，那么滤波后的图像就会比原图像更亮，反之，如果小于1，那么得到的图像就会变暗。如果和为0，图像不会变黑，但也会非常暗。

4）对于滤波后的结构，可能会出现负数或者大于255的数值。对这种情况，我们将他们直接截断到0和255之间即可。对于负数，也可以取绝对值。

　　常见的卷积核：

soble_x = np.array(([-1, 0, 1], [-2, 0, 2], [-1, 0, 1]))
soble_y = np.array(([-1, -2, -1], [0, 0, 0], [1, 2, 1]))
soble = np.array(([-1, -1, 0], [-1, 0, 1], [0, 1, 1]))
prewitt_x = np.array(([-1, 0, 1], [-1, 0, 1], [-1, 0, 1]))
prewitt_y = np.array(([-1, -1,-1], [0, 0, 0], [1, 1, 1]))
prewitt = np.array(([-2, -1, 0], [-1, 0, 1], [0, 1, 2]))
laplacian = np.array(([0, -1, 0], [-1, 4, -1], [0, -1, 0]))
laplacian2 = np.array(([-1, -1, -1], [-1, 8, -1], [-1, -1, -1]))

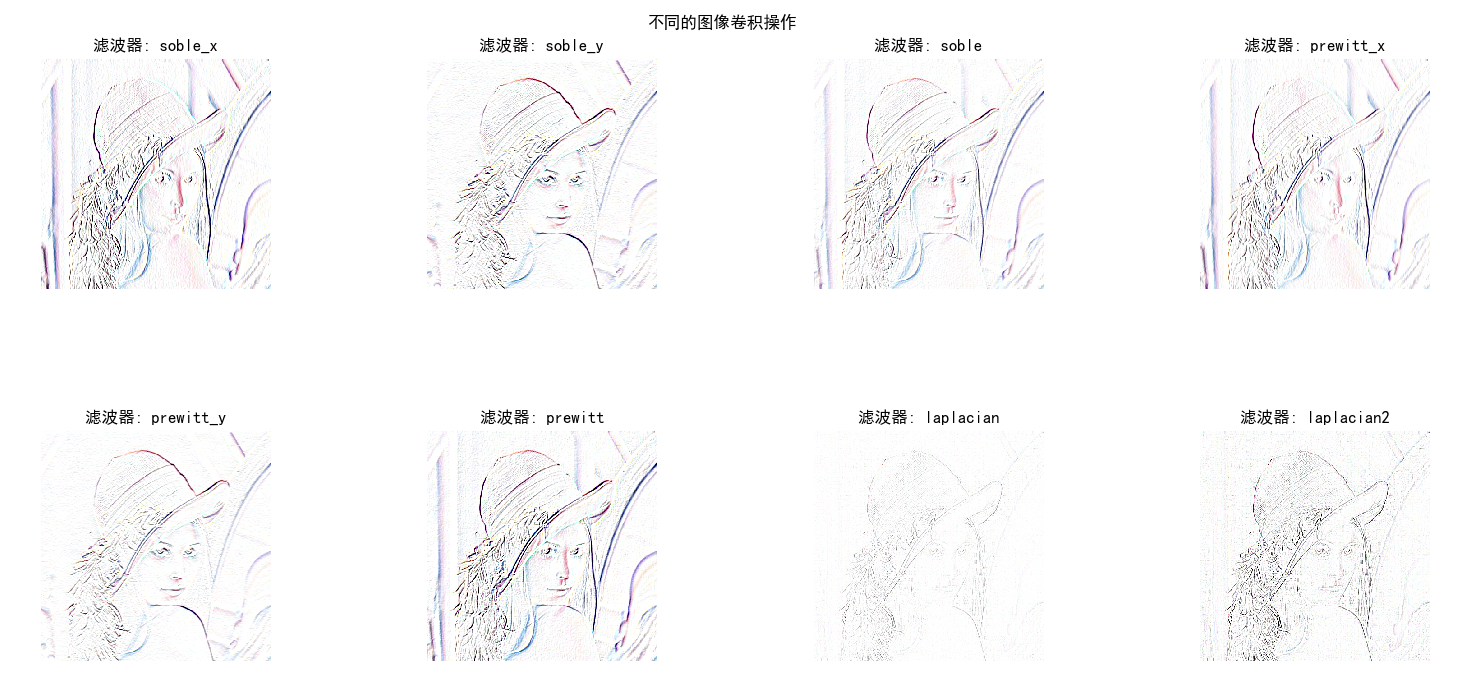
　　不同的卷积核对图像进行滤波得到的效果是不同的，我们可以根据滤波器的特点分析出滤波器的功能，下面我们使用python代码对卷积操作进行实践：

import numpy as np
from PIL import Image
import matplotlib.pyplot as plt
import matplotlib as mpl

def convolve(image, filt):
    height, width = image.shape
    h, w = filt.shape
    height_new = height - h + 1
    width_new = width - w + 1
    image_new = np.zeros((height_new, width_new), dtype=np.float)
    for i in range(height_new):
        for j in range(width_new):
            image_new[i,j] = np.sum(image[i:i+h, j:j+w] * filt)
    image_new = image_new.clip(0, 255)
    image_new = np.rint(image_new).astype('uint8')
    return image_new

if __name__ == "__main__":
    mpl.rcParams['font.sans-serif'] = ['SimHei']
    mpl.rcParams['axes.unicode_minus'] = False

    path = './simplepython/convolve/lena.png'
    A = Image.open(path, 'r')
    a = np.array(A)
    soble_x = np.array(([-1, 0, 1], [-2, 0, 2], [-1, 0, 1]))
    soble_y = np.array(([-1, -2, -1], [0, 0, 0], [1, 2, 1]))
    soble = np.array(([-1, -1, 0], [-1, 0, 1], [0, 1, 1]))
    prewitt_x = np.array(([-1, 0, 1], [-1, 0, 1], [-1, 0, 1]))
    prewitt_y = np.array(([-1, -1,-1], [0, 0, 0], [1, 1, 1]))
    prewitt = np.array(([-2, -1, 0], [-1, 0, 1], [0, 1, 2]))
    laplacian = np.array(([0, -1, 0], [-1, 4, -1], [0, -1, 0]))
    laplacian2 = np.array(([-1, -1, -1], [-1, 8, -1], [-1, -1, -1]))
    weight_list = ('soble_x', 'soble_y', 'soble', 'prewitt_x', 'prewitt_y', 'prewitt', 'laplacian', 'laplacian2')
    plt.figure(figsize=(10,4))
    i = 1
    for weight in weight_list:
        R = convolve(a[:, :, 0], eval(weight))
        G = convolve(a[:, :, 1], eval(weight))
        B = convolve(a[:, :, 2], eval(weight))
        I = 255 - np.stack((R, G, B), 2)

        plt.subplot(2, 4, i)
        i += 1
        plt.title("滤波器: %s"%(weight))
        plt.axis('off')
        plt.imshow(I)
    plt.tight_layout(2)
    plt.subplots_adjust(top=0.92)
    plt.suptitle('不同的图像卷积操作')
    plt.show()

　　上述代码中，image_new.clip(0, 255)函数的作用是将image_new中的值进行截断，小于等于0的置为0，大于等于255的置为255。np.rint(image_new).astype('uint8')的含义是将得到的图像矩阵转换为int型，在转换为uint8类型。eval(weight)函数的作用是将字符串值转换为对应的变量值。我们对lena图像进行操作，下面是得到的结果：