[CTSC2017]网络

[CTSC2017]网络

连一条长度为len的边，使得基环树的直径最小

结论：一定连在某条直径两个点上（否则更靠近不劣）

然后二分答案判定。

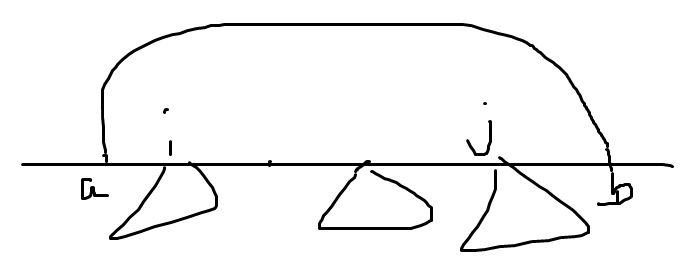
dp[i]：链上一个点往下延伸的最大深度

考虑对于任意两个点对最短路径都不能大于mid

就是：任意的(i<j)，min(sum[j]-sum[i]+dp[i]+dp[j],len+|sumb-sumj|+|sumi-suma|+dp[i]+dp[j])<mid

前面的min比较好处理，直接按照sum+dp,dp-sum排序，双指针搞一下

不能满足前面的min的点对i，j，必然要满足后面的。

把绝对值拆开成4个，对于任意的i，j，选择的a，b都要使得这些4*k个不等式成立。

suma,sumb移项，所以4个不等式右边都要取最大的（任意转化为最值）

所以双指针的时候可以再用树状数组（为了i<j）找到4个lim

然后移项。

枚举b，sum升序降序排序，四指针维护。

每次看区间的交是否为空。

#include<bits/stdc++.h>
#define reg register int
#define il inline
#define fi first
#define se second
#define mk(a,b) make_pair(a,b)
#define numb (ch^'0')
using namespace std;
typedef long long ll;
template<class T>il void rd(T &x){
    char ch;x=;bool fl=false;
    while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true);
    for(x=numb;isdigit(ch=getchar());x=x*+numb);
    (fl==true)&&(x=-x);
}
template<class T>il void output(T x){if(x/)output(x/);putchar(x%+'');}
template<class T>il void ot(T x){if(x<) putchar('-'),x=-x;output(x);putchar(' ');}
template<class T>il void prt(T a[],int st,int nd){for(reg i=st;i<=nd;++i) ot(a[i]);putchar('\n');}

namespace Miracle{
const int N=1e5+;
const ll inf=0x3f3f3f3f3f3f3f3f;
int n;
struct node{
    int nxt,to;
    int val;
}e[*N];
int hd[N],cnt;
void add(int x,int y,int z){
    e[++cnt].nxt=hd[x];
    e[cnt].to=y;
    e[cnt].val=z;
    hd[x]=cnt;
}
ll ans,len;
ll L,R;
int mem[N],fa[N],vf[N];
int on[N];
ll sum[N];
struct po{
    ll v;
    int id;
    po(){}
    po(ll vv,int dd){
        v=vv;id=dd;
    }
};
struct qs{
    po p[N];
    int sz;
    void push(ll v,int d){
        p[++sz]=po(v,d);
    }
    void clear(){
        sz=;
    }
    il po &operator[](const int &x){return p[x];}
    il const po &operator[](const int &x) const {return p[x];}
}su,sd,up,dw;//member's number is num

bool cmpu(po a,po b){//sheng
    return a.v<b.v;
}
bool cmpd(po a,po b){//jiang
    return a.v>b.v;
}
int st,nd,num;
ll mx;
struct tr{
    ll f[N];
    void clear(){
        memset(f,-0x3f,sizeof f);
    }
    void ins(int x,ll v){
        for(;x<=n;x+=x&(-x)) f[x]=max(f[x],v);
    }
    ll query(int x){
        ll ret=-inf;
        for(;x;x-=x&(-x)) ret=max(ret,f[x]);
        return ret;
    }
}t[];
//t[0]:dp-sum
//t[1]:dp+sum
void dfs1(int x,ll dis){
    if(dis>mx) {
        mx=dis;st=x;
    }
    for(reg i=hd[x];i;i=e[i].nxt){
        int y=e[i].to;
        if(y==fa[x]) continue;
        fa[y]=x;
        dfs1(y,dis+e[i].val);
    }
}
void dfs2(int x,ll dis){
    if(dis>mx){
        mx=dis;nd=x;
    }
    for(reg i=hd[x];i;i=e[i].nxt){
        int y=e[i].to;
        if(y==fa[x]) continue;
        fa[y]=x;
        vf[y]=e[i].val;
        dfs2(y,dis+e[i].val);
    }
}
ll dp[N];
void fin(int x){
    dp[x]=;
    for(reg i=hd[x];i;i=e[i].nxt){
        int y=e[i].to;
        if(y==fa[x]||on[y]) continue;
        fa[y]=x;
        fin(y);
        L=max(L,dp[x]+dp[y]+e[i].val);
        dp[x]=max(dp[x],dp[y]+e[i].val);
    }
}
struct pointer{
    int ptr;
    ll lim;
    void clear(){
        ptr=;lim=-inf;
    }
    void upda(ll v){
        lim=max(lim,v);
    }
}p[];
pair<int,int>tp;
void con(int l,int r){
    tp.fi=max(tp.fi,l);
    tp.se=min(tp.se,r);
}
bool che(ll mid){
    ///warning!!!! dp[mem[...[].id]]
    t[].clear();t[].clear();
    for(reg i=;i<=;++i) p[i].clear();
    int ptr=;
    for(reg j=;j<=num;++j){
        while(ptr<num&&dw[ptr+].v+up[j].v>mid) {
            ++ptr;
            t[].ins(dw[ptr].id,dw[ptr].v);
            t[].ins(dw[ptr].id,sum[dw[ptr].id]+dp[mem[dw[ptr].id]]);
        }
        if(ptr){
            ll djss=dp[mem[up[j].id]]-sum[up[j].id],djas=up[j].v;
            ll diss=t[].query(up[j].id-),dias=t[].query(up[j].id-);
            p[].upda(len-mid+djss+dias);
            p[].upda(len-mid+diss+djas);
            p[].upda(len-mid+dias+djas);
            p[].upda(len-mid+diss+djss);
        }
    }
    p[].ptr=p[].ptr=;
    for(reg b=;b<=num;++b){
        while(p[].ptr<=num&&su[p[].ptr].v-p[].lim<su[b].v) ++p[].ptr;
        while(p[].ptr<num&&su[p[].ptr+].v+p[].lim<=su[b].v) ++p[].ptr;
        while(p[].ptr<num&&-sd[p[].ptr+].v+p[].lim<=su[b].v) ++p[].ptr;
        while(p[].ptr<=num&&-sd[p[].ptr].v-p[].lim<su[b].v) ++p[].ptr;
        tp.fi=;tp.se=num;
        con(p[].ptr,num);
        con(,p[].ptr);
        con(num-p[].ptr+,num);
        con(,num-p[].ptr+);
        if(tp.fi<=tp.se) return true;
    }
    return false;
    ///warning!!!! dp[mem[...[].id]]
}
void clear(){
    ans=inf;num=;st=nd=;
    memset(sum,,sizeof sum);
    memset(fa,,sizeof fa);
    memset(vf,,sizeof vf);
    memset(on,,sizeof on);
    memset(hd,,sizeof hd);
    su.clear();sd.clear();up.clear();dw.clear();
    cnt=;
    L=,R=;
}
int main(){
    while(){
        clear();
        rd(n);rd(len);
        if(n==&&len==) break;
        mx=-;
        int x,y,z;
        for(reg i=;i<n;++i){
            rd(x);rd(y);rd(z);
            add(x,y,z);add(y,x,z);
        }
        if(n==){
            puts("");continue;
        }
        dfs1(,);
        fa[st]=;
        mx=-;
        dfs2(st,);
/*RRR*/ R=mx;
        num=;
        x=nd;
        while(x){
            mem[++num]=x;
            on[x]=;
            sum[num]=sum[num-]+vf[mem[num-]];
            x=fa[x];
        }
        memset(fa,,sizeof fa);
/*LLL*/ for(reg i=;i<=num;++i){
            fin(mem[i]);
        }

        for(reg i=;i<=num;++i){
            su.push(sum[i],i);
            sd.push(sum[i],i);
            up.push(dp[mem[i]]+sum[i],i);
            dw.push(dp[mem[i]]-sum[i],i);
        }
        sort(su.p+,su.p+num+,cmpu);
        sort(sd.p+,sd.p+num+,cmpd);
        sort(up.p+,up.p+num+,cmpu);
        sort(dw.p+,dw.p+num+,cmpd);

        while(L<=R){
            ll mid=(L+R)/;
            if(che(mid)){
                ans=mid;R=mid-;
            }else L=mid+;
        }
        printf("%lld\n",ans);
    }
    return ;
}

}
signed main(){
    Miracle::main();
    return ;
}

/*
   Author: *Miracle*
*/

二分判定突破口

判定min的或关系。不涉及a,b的先去掉，对于剩下的任意变成最值，纯粹解不等式了。

大量运用排序+双指针。