数字IC设计流程
数字IC设计流程
简单介绍数字IC设计流程
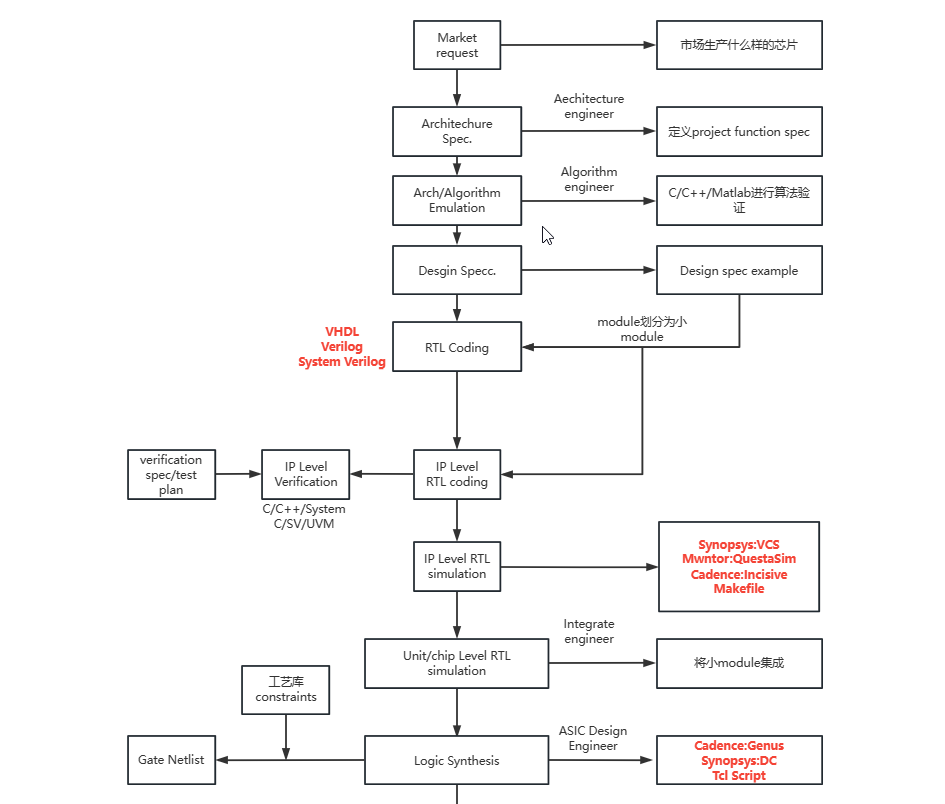
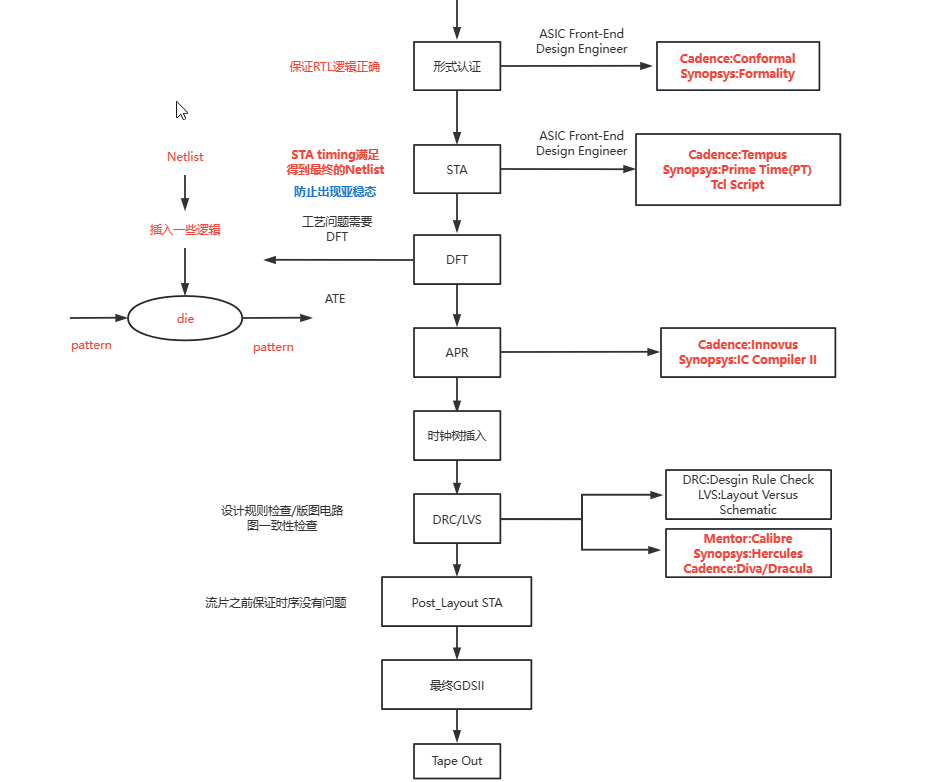
数字IC设计流程的更多相关文章
- VerilogHDL概述与数字IC设计流程学习笔记
一.HDL的概念和特征 HDL,Hard Discrimination Language的缩写,翻译过来就是硬件描述语言.那么什么是硬件描述语言呢?为什么不叫硬件设计语言呢?硬件描述语言,顾名思义就是 ...
- 【转载】数字IC设计流程及开发工具
原文链接:https://www.zhihu.com/question/28322269/answer/42048070 Design Flow <img src="h ...
- 数字IC设计工程师的知识结构
刚毕业的时候,我年少轻狂,以为自己已经可以独当一面,庙堂之上所学已经足以应付业界需要.然而在后来的工作过程中,我认识了很多牛人,也从他们身上学到了很多,从中总结了一个IC设计工程师需要具备的知识架构, ...
- 数字IC设计入门书单
首发于观芯志 写文章 数字IC设计入门书单 Forever snow 1 年前 作者:Forever snow链接:你所在领域的入门书单? - 知乎用户的回答来源:知乎著作权归作者所有,转 ...
- IC设计流程介绍
芯片设计分为前端设计和后端设计,前端设计(也称逻辑设计)和后端设计(也称物理设计)并没有统一严格的界限,涉及到与工艺有关的设计就是后端设计. 1. 规格制定 芯片规格,也就像功能列表一样 ...
- IC设计流程概述
芯片设计分为前端设计和后端设计,前端设计(也称逻辑设计)和后端设计(也称物理设计)并没有统一严格的界限,涉及到与工艺有关的设计就是后端设计. Front-end design flow 1. 规格制定 ...
- 数字IC设计入门必备——VIM自定义模板调用与VCS基本仿真操作示例
一.前言 毕业论文答辩结束,闲下来写篇文章.芯片研发人员都在Linux系统下借助各种EDA工具和代码语言完成工作,因此提高代码开发效率,熟练运用开发工具是十分必要的.本文讲述VIM编辑神器的veril ...
- 数字IC设计-15-DPI(延续)
简介 供SV,无论是构建测试激励,或模拟硬件的并行行为,DPI这是非常方便.上次我们介绍SV内通"import"导入和电话C性能. 在本节,通过一个简单的例子来说明C什么语言的函数 ...
- 数字IC设计工程师成长之路
学习的课程 仿真工具VCS实践学习 2019年12月9日-2019年12月23日
- 数字IC前后端设计中的时序收敛(五)--Max Transition违反的修复方法
本文转自:自己的微信公众号<数字集成电路设计及EDA教程> 里面主要讲解数字IC前端.后端.DFT.低功耗设计以及验证等相关知识,并且讲解了其中用到的各种EDA工具的教程. 考虑到微信公众 ...
随机推荐
- Vue学习之--------监视属性(2022/7/10)
文章目录 1.监视属性 1.1 监视属性--天气案例 1.1.1 基础知识 1.1.2 代码实例 1.1.2 测试效果 1.2 深度监视-天气案例 1.2.1 基础知识 1.2.2 代码实例 1.2. ...
- servlet过滤器--使用过滤器统计网站访问人数的计数(注解形式)
文章目录 1.什么是过滤器? 2.过滤器核心对象 3.过滤器创建和配置 4.举例子 1.什么是过滤器? 主要用于对客户端的请求进行过滤处理,再将经过过滤后的请求转交给下一个资源. 2.过滤器核心对象 ...
- 使用python获取window注册表值的方法
提供regfullpath的方法,可以自行封装个regpath的函数import loggingimport pywintypes import win32apiimport win32con def ...
- UEC 利用代理/委托写一个生命组件
首先基于ActorComponent创建一个组件 HealthComponent,将需要的变量与函数创建 #include "CoreMinimal.h" #include &qu ...
- Python基础之函数:4、二分法、三元表达式、生成/推导式、匿名函数、内置函数
目录 一.算法简介之二分法 1.什么是算法 2.算法的应用场景 3.二分法 二.三元表达式 1.简介及用法 三.各种生成式 1.列表生成式 2.字典生成式 3.集合生成式 四.匿名函数 五.常见内置函 ...
- 云原生之旅 - 7)部署Terrform基础设施代码的自动化利器 Atlantis
前言 前面有几篇文章讲述了如何使用Terraform创建资源 (基础设施即代码 Terraform 快速入门, 使用 Terraform 创建 Kubernetes) 以及 Kubernetes时代的 ...
- 为什么 softmax 计算时要先减去最大值
根据 softmax 最基本的定义,计算公式如下所示: $$S_i=\frac{e^{x_i}}{\sum_j e^{x_j}}$$ 原理也很简单,将原向量变为分布的形式(和为1). 看似很美好,但是 ...
- 【题解】CF356A Knight Tournament
题面传送门 本蒟蒻想练习一下并查集,所以是找并查集标签来这里的.写题解加深理解. 解决思路 自然,看到区间修改之类很容易想到线段树,但本蒟蒻线段树会写挂,所以这里就讲比较简单的并查集思路. 并查集的核 ...
- 数据库json字段类型总结
----------------------------------------=================以下是个人自己总结,可能只有自己看的懂.===================---- ...
- 利用KubeEdge在A500部署边缘推理任务
利用KubeEdge在A500部署边缘推理任务 目 录 1 环境介绍... 1 2 云端环境部署... 2 2.1 在master节点安装Docker和k8S (ubuntu) 2 2.1.1 ...
