动态规划——leetcode5、最长回文子串
1、题目描述:
2、解题方法:动态规划
动态规划解题步骤:
1、确定状态
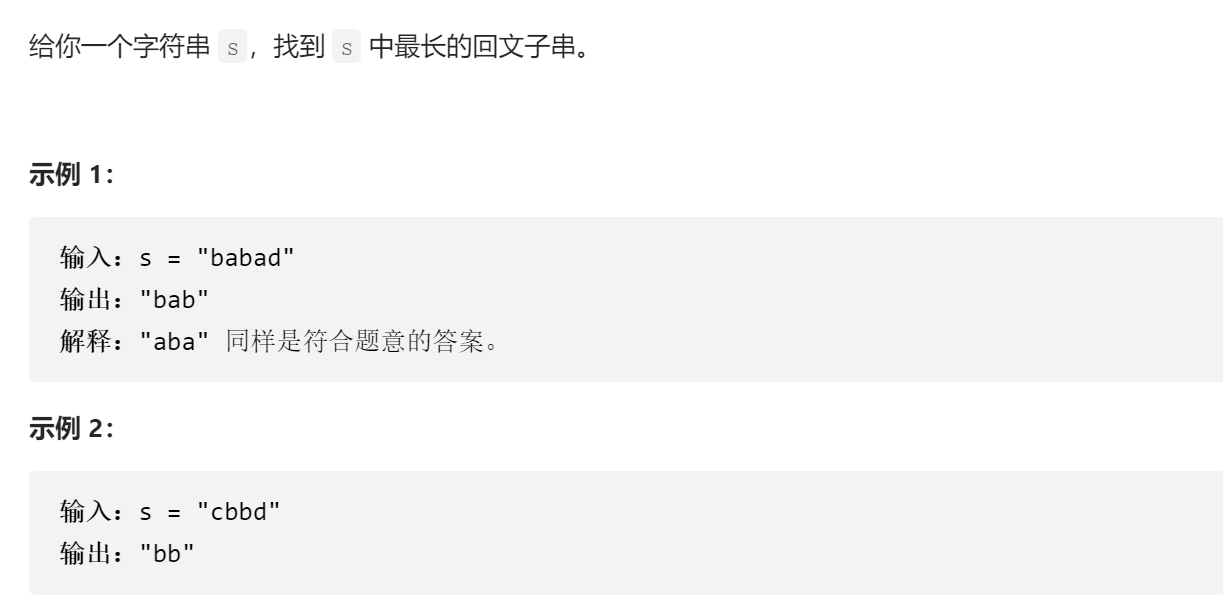
- 最后一步:如果s[i,...,j]是回文子串,那么需要满足两个条件
① s[i] == s[j];
② s[i+1,...,j-1]是回文子串;
- 子问题:我们要验证s[i+1,...,j-1]是不是回文子串
- 用dp[i][j]来表示s[i,...,j]是不是回文子串
2、转移方程
dp[i][j] = (s[i] == s[j])&& dp[i+1][j-1]
3、初始条件和边界情况
初始条件:dp[i][i] == true;
边界条件:在s[i] == s[j]的条件下,j-i<=2或者j-i<3,即说明s[i,...,j]的长度为2或者是3时,不用检查是不是回文串。
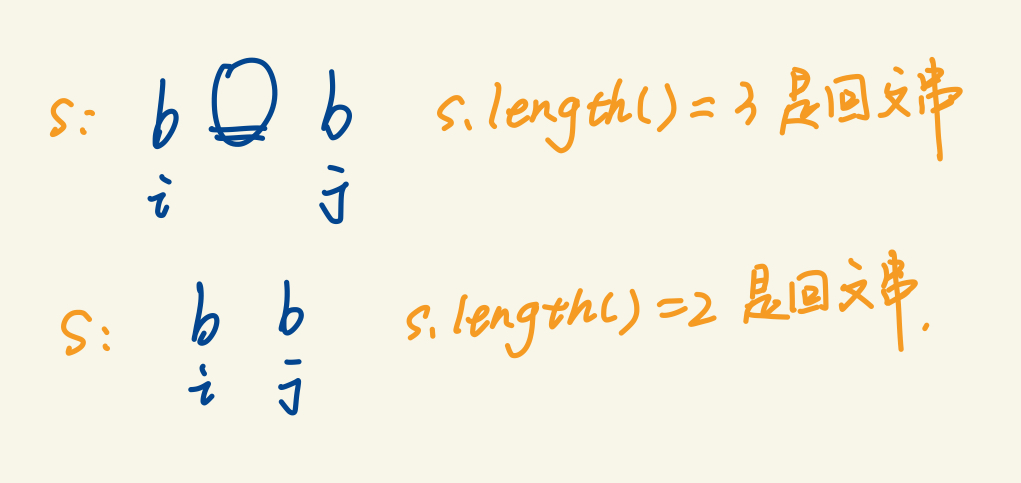
4、计算顺序
以字符串s:babab为例,一列一列的进行填表,先升序填列,再升序填行。
3、代码:
public String longestPalindrome(String s) {
int len = s.length();
if(len < 2){
return s;
}
int maxLen = 1;
int start = 0;
char[] res = s.toCharArray();
boolean[][] dp = new boolean[len][len];
for(int i = 0; i < len; i++){
dp[i][i] = true;
}
for(int j = 1; j < len; j++){
for(int i = 0; i < j; i++){
if(res[i] == res[j]){
if(j - i < 3 || dp[i+1][j-1] == true){
dp[i][j] = true;
}
if( j-i+1 > maxLen && dp[i][j] == true){
maxLen = j-i+1;
start = i;
}
}
}
}
return s.substring(start,start + maxLen);
}
动态规划——leetcode5、最长回文子串的更多相关文章
- leetcode-5 最长回文子串(动态规划)
题目要求: * 给定字符串,求解最长回文子串 * 字符串最长为1000 * 存在独一无二的最长回文字符串 求解思路: * 回文字符串的子串也是回文,比如P[i,j](表示以i开始以j结束的子串)是回文 ...
- LeetCode5 最长回文子串
最长回文子串 给定一个字符串 s,找到 s 中最长的回文子串.你可以假设 s 的最大长度为 1000. 示例 1: 输入: "babad" 输出: "bab" ...
- [Swift]LeetCode5. 最长回文子串 | Longest Palindromic Substring
Given a string s, find the longest palindromic substring in s. You may assume that the maximum lengt ...
- LeetCode5.最长回文子串 JavaScript
给定一个字符串 s,找到 s 中最长的回文子串.你可以假设 s 的最大长度为 1000. 示例 1: 输入: "babad" 输出: "bab" 注意: &qu ...
- 5. Longest Palindromic Substring(最长回文子串 manacher 算法/ DP动态规划)
Given a string s, find the longest palindromic substring in s. You may assume that the maximum lengt ...
- 【LeetCode】最长回文子串【动态规划或中心扩展】
给定一个字符串 s,找到 s 中最长的回文子串.你可以假设 s 的最大长度为 1000. 示例 1: 输入: "babad"输出: "bab"注意: " ...
- Leetcode(5)-最长回文子串(包含动态规划以及Manacher算法)
给定一个字符串 s,找到 s 中最长的回文子串.你可以假设 s 的最大长度为1000. 示例 1: 输入: "babad" 输出: "bab" 注意: &quo ...
- [LeetCode] 5. 最长回文子串 ☆☆☆(最长子串、动态规划)
最长回文子串 (动态规划法.中心扩展算法) https://leetcode-cn.com/problems/longest-palindromic-substring/solution/xiang- ...
- leetcode5 最长回文字符串 动态规划 Manacher法
dp 注意没有声明S不空,处理一下 o(n^2) class Solution { public: string longestPalindrome(string s) { if (s.empty() ...
- [译]最长回文子串(Longest Palindromic Substring) Part I
[译]最长回文子串(Longest Palindromic Substring) Part I 英文原文链接在(http://leetcode.com/2011/11/longest-palindro ...
随机推荐
- vscode远程调试c++
0.背景 最近在学习linux webserver开发,需要在linux下调试自己的C/C++代码,但是linux下不像在windows下,直接Visio Studio或者其它集成开发环境那么方便,现 ...
- WindowsServer评估版转为正式版并激活
更新记录 本文迁移自Panda666原博客,原发布时间:2021年5月16日. 一般从官网下载的Windows Server版本都是评估试用版本.这时候想转为正式版本,就需要使用转换激活代码.请参照不 ...
- SAP Context menu(菜单)
*&---------------------------------------------------------------------* *& Report RSDEMO_CO ...
- 使用vue实现排序算法演示动画
缘起 最近做的一个小需求涉及到排序,界面如下所示: 因为项目是使用vue的,所以实现方式很简单,视图部分不用管,本质上就是操作数组,代码如下: { // 上移 moveUp (i) { // 把位置i ...
- static关键字续、继承、重写、多态
static关键字 1.对于实例变量,每个java对象都拥有自己的一份,存储在堆内存当中,在构造方法执行的时候初始化. 2.所有对象都拥有同一个属性时,并且值相同,建议声明为static变量. 3.静 ...
- 把excel的数据导入到SQLSERVER里面,excel的字符串时间在导入sql库显示datetime 数据类型的转换产生一个超出范围的值
这是我Excel导入的数据,准备把这个varchar(50)时间导入我的userInfo表中的出生日期字段datatime,如果你的数据正常,是可以导入的, 但是有些日期可能超出datatime的最大 ...
- Static、Final关键字详解
1.Static 详情见下面代码讲解 点击查看代码 package com.Tang.oop.demo07; public class Student { private static int age ...
- C#(.net) 面试题
1.ASP.NET的页面生存周期 .aspx/.ashx->IIS->Asp.net_isapi.dll->HttpRuntime.ProcessRequest() ->Htt ...
- 40+倍提升,详解 JuiceFS 元数据备份恢复性能优化之路
JuiceFS 支持多种元数据存储引擎,且各引擎内部的数据管理格式各有不同.为了便于管理,JuiceFS 自 0.15.2 版本提供了 dump 命令允许将所有元数据以统一格式写入到 JSON 文件进 ...
- 5-20 Web服务器和Nginx
什么是Web服务器 简单来说 Web服务器就是一个能够接收http请求并作出响应的java程序 我们再二阶段编写的webServer项目其实就是我们手写的Web服务器 我们现在开发的标准SpringB ...
