cryptohack wp day(4)
接上题
第五题(Modular Inverting)

在模运算中,如果我们要解决形如a * x ≡ b mod m的方程,其中a,b,m是已知整数,x是未知整数,我们可以使用扩展欧几里得算法来找到x的值。但是,如果m是一个质数,我们可以使用费马小定理来计算a的逆元,即a关于模m的倒数。
具体来说,如果p是一个素数,a是p的倍数之外的任意整数,那么a的逆元a^-1就是满足下列等式的整数b:
a * b ≡ 1 mod p
这里,b就是a在模p意义下的逆元。例如,假设我们要求解3在模13意义下的逆元,也就是找到一个整数b满足3 * b ≡ 1 mod 13。根据费马小定理,3^11 ≡ 1 mod 13,因此3的逆元就是3^10,即9。因为3 * 9 ≡ 1 mod 13。
综上所述,如果我们知道一个数a在模p意义下的逆元b,那么我们就可以用a * b ≡ 1 mod p来验证b是不是a的逆元,也可以用a * b对p取模来计算a在模p意义下的倒数。
python代码如下:
def find_inverse(a, p):
"""
使用费马小定理计算a在模p意义下的逆元。
"""
if gcd(a, p) != 1:
raise ValueError("a和p必须互质")
return pow(a, p-2, p)
def gcd(a, b):
"""
使用欧几里得算法计算a和b的最大公因数。
"""
if b == 0:
return a
else:
return gcd(b, a % b)
print(find_inverse(3,13))
第六题(Quadratic Residues)
在模块化算术中,模平方剩余 (QR) 是一个整数,它与完全平方模某个整数模的整数全等。更正式地说,如果存在整数 x,则整数 a 是对整数 p 取模的二次留数,使得:
x^2 ≡ a (mod p)
如果这样的整数 x 存在,我们说 a 是二次留数模 p 并写成 a ≡ x^2 (mod p)。
如果不存在这样的整数 x,则 a 称为二次无余数模 p。
所有二次留数模 p 的集合用 QR(p) 表示,所有二次模非平方剩余 p 的集合用 QNR(p) 表示。
确定一个整数是二次剩余还是非剩余模给定素数 p 是数论中的一个重要问题,在密码学、编码理论和其他领域有各种应用。二次互易定律提供了一个强大的工具来确定二次留数和非留数模素数,以及计算勒让德符号,勒让德符号是一个相关的数学函数,可用于确定二次留数和非留数对任何奇数取模。
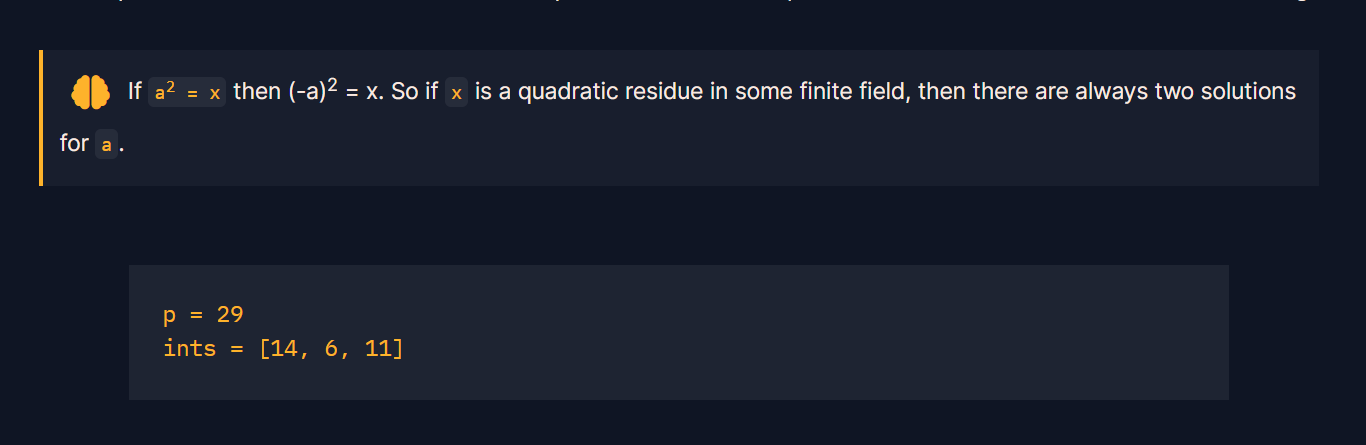
题目给了p = 29 , i n ts = [ 14 , 6 , 11 ],找到三个书中的QR的那一个,解出这个数的模平方根,小的一个根即flag.
上代码:
def quad_residue(x, p):
"""
检查 x 是否是有限域 F_p 中的二次留数。
如果 x 是二次剩余,则返回 True,否则返回 False。
"""
for a in range(1, p):
if pow(a, 2, p) == x:
return True
return False
def solve_quad_residue(x, p):
"""
在有限域 F_p 中求解方程 a^2 = x,其中 p 是质数模数。
返回两个解的元组(如果存在),如果 x 不是二次残差则返回 None。
"""
if not quad_residue(x, p):
return None
solutions = []
for a in range(1, p):
if pow(a, 2, p) == x:
solutions.append(a)
solutions.append(p - a) # 添加负解
break
return tuple(solutions)
p = 29
ints = [14, 6, 11]
for x in ints:
print(f"x = {x}")
solutions = solve_quad_residue(x, p)
if solutions:
print(f"Solutions: {solutions}")
else:
print("Not a quadratic residue")
第七题(Legendre Symbol)
p = 101524035174539890485408575671085261788758965189060164484385690801466167356667036677932998889725476582421738788500738738503134356158197247473850273565349249573867251280253564698939768700489401960767007716413932851838937641880157263936985954881657889497583485535527613578457628399173971810541670838543309159139
ints = [25081841204695904475894082974192007718642931811040324543182130088804239047149283334700530600468528298920930150221871666297194395061462592781551275161695411167049544771049769000895119729307495913024360169904315078028798025169985966732789207320203861858234048872508633514498384390497048416012928086480326832803, 45471765180330439060504647480621449634904192839383897212809808339619841633826534856109999027962620381874878086991125854247108359699799913776917227058286090426484548349388138935504299609200377899052716663351188664096302672712078508601311725863678223874157861163196340391008634419348573975841578359355931590555, 17364140182001694956465593533200623738590196990236340894554145562517924989208719245429557645254953527658049246737589538280332010533027062477684237933221198639948938784244510469138826808187365678322547992099715229218615475923754896960363138890331502811292427146595752813297603265829581292183917027983351121325, 14388109104985808487337749876058284426747816961971581447380608277949200244660381570568531129775053684256071819837294436069133592772543582735985855506250660938574234958754211349215293281645205354069970790155237033436065434572020652955666855773232074749487007626050323967496732359278657193580493324467258802863, 4379499308310772821004090447650785095356643590411706358119239166662089428685562719233435615196994728767593223519226235062647670077854687031681041462632566890129595506430188602238753450337691441293042716909901692570971955078924699306873191983953501093343423248482960643055943413031768521782634679536276233318, 85256449776780591202928235662805033201684571648990042997557084658000067050672130152734911919581661523957075992761662315262685030115255938352540032297113615687815976039390537716707854569980516690246592112936796917504034711418465442893323439490171095447109457355598873230115172636184525449905022174536414781771, 50576597458517451578431293746926099486388286246142012476814190030935689430726042810458344828563913001012415702876199708216875020997112089693759638454900092580746638631062117961876611545851157613835724635005253792316142379239047654392970415343694657580353333217547079551304961116837545648785312490665576832987, 96868738830341112368094632337476840272563704408573054404213766500407517251810212494515862176356916912627172280446141202661640191237336568731069327906100896178776245311689857997012187599140875912026589672629935267844696976980890380730867520071059572350667913710344648377601017758188404474812654737363275994871, 4881261656846638800623549662943393234361061827128610120046315649707078244180313661063004390750821317096754282796876479695558644108492317407662131441224257537276274962372021273583478509416358764706098471849536036184924640593888902859441388472856822541452041181244337124767666161645827145408781917658423571721, 18237936726367556664171427575475596460727369368246286138804284742124256700367133250078608537129877968287885457417957868580553371999414227484737603688992620953200143688061024092623556471053006464123205133894607923801371986027458274343737860395496260538663183193877539815179246700525865152165600985105257601565]
考察二次剩余定理
二次剩余定理表述如下:如果p和q是两个不同的奇素数,则二次剩余x mod p可以通过奇偶性以及符号确定它是否是二次剩余mod q,具体来说:
如果p和q都是形如4k+1的素数,或者都是形如4k+3的素数,则x mod p是二次剩余mod q当且仅当q mod p是二次剩余mod p。
如果p是形如4k+1的素数,q是形如4k+3的素数,则x mod p是二次剩余mod q当且仅当q mod p是二次非剩余mod p。
如果p是形如4k+3的素数,q是形如4k+1的素数,则x mod p是二次剩余mod q当且仅当q mod p是二次剩余mod p。
二次剩余
x^2≡n(mod p)
对于这个方程,求出满足的x.

想要更好了解,推荐下:
再看这道题,直接上代码:
p = 101524035174539890485408575671085261788758965189060164484385690801466167356667036677932998889725476582421738788500738738503134356158197247473850273565349249573867251280253564698939768700489401960767007716413932851838937641880157263936985954881657889497583485535527613578457628399173971810541670838543309159139
ints = [25081841204695904475894082974192007718642931811040324543182130088804239047149283334700530600468528298920930150221871666297194395061462592781551275161695411167049544771049769000895119729307495913024360169904315078028798025169985966732789207320203861858234048872508633514498384390497048416012928086480326832803, 45471765180330439060504647480621449634904192839383897212809808339619841633826534856109999027962620381874878086991125854247108359699799913776917227058286090426484548349388138935504299609200377899052716663351188664096302672712078508601311725863678223874157861163196340391008634419348573975841578359355931590555, 17364140182001694956465593533200623738590196990236340894554145562517924989208719245429557645254953527658049246737589538280332010533027062477684237933221198639948938784244510469138826808187365678322547992099715229218615475923754896960363138890331502811292427146595752813297603265829581292183917027983351121325, 14388109104985808487337749876058284426747816961971581447380608277949200244660381570568531129775053684256071819837294436069133592772543582735985855506250660938574234958754211349215293281645205354069970790155237033436065434572020652955666855773232074749487007626050323967496732359278657193580493324467258802863, 4379499308310772821004090447650785095356643590411706358119239166662089428685562719233435615196994728767593223519226235062647670077854687031681041462632566890129595506430188602238753450337691441293042716909901692570971955078924699306873191983953501093343423248482960643055943413031768521782634679536276233318, 85256449776780591202928235662805033201684571648990042997557084658000067050672130152734911919581661523957075992761662315262685030115255938352540032297113615687815976039390537716707854569980516690246592112936796917504034711418465442893323439490171095447109457355598873230115172636184525449905022174536414781771, 50576597458517451578431293746926099486388286246142012476814190030935689430726042810458344828563913001012415702876199708216875020997112089693759638454900092580746638631062117961876611545851157613835724635005253792316142379239047654392970415343694657580353333217547079551304961116837545648785312490665576832987, 96868738830341112368094632337476840272563704408573054404213766500407517251810212494515862176356916912627172280446141202661640191237336568731069327906100896178776245311689857997012187599140875912026589672629935267844696976980890380730867520071059572350667913710344648377601017758188404474812654737363275994871, 4881261656846638800623549662943393234361061827128610120046315649707078244180313661063004390750821317096754282796876479695558644108492317407662131441224257537276274962372021273583478509416358764706098471849536036184924640593888902859441388472856822541452041181244337124767666161645827145408781917658423571721, 18237936726367556664171427575475596460727369368246286138804284742124256700367133250078608537129877968287885457417957868580553371999414227484737603688992620953200143688061024092623556471053006464123205133894607923801371986027458274343737860395496260538663183193877539815179246700525865152165600985105257601565]
solution = []
for a in ints:
result = pow(a,(p-1)//2,p)
if result == 1:
solution.append(ints.index(a))
print(solution)
flag = pow(a,(p+1)//4,p)
print("flag=",flag)
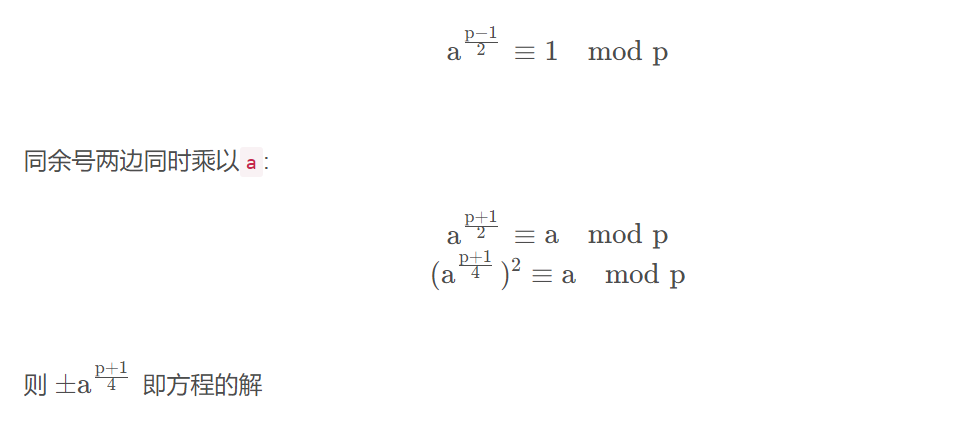
cryptohack wp day(4)的更多相关文章
- 逆天通用水印支持Winform,WPF,Web,WP,Win10。支持位置选择(9个位置 ==》[X])
常用技能:http://www.cnblogs.com/dunitian/p/4822808.html#skill 逆天博客:http://dnt.dkil.net 逆天通用水印扩展篇~新增剪贴板系列 ...
- wp已死,metro是罪魁祸首!
1.这篇文章肯定会有类似这样的评论:“我就是喜欢wp,我就是喜欢metro,我就是软粉“等类似的信仰论者发表的评论. 2.2014年我写过一篇文章,windows phone如何才能在中国翻身? 我现 ...
- 关于 WP 开发中.xaml 与.xaml.cs 的关系
今天我们先来看一下在WP8.1开发中最长见到的几个文件之间的关系.比较论证,在看这个问题之前我们简单看看.NET平台其他两个不同的框架: Windows Forms 先看看Window Forms中的 ...
- Android,ios,WP三大手机系统对比
从前,我以为.一个手机系统只是一个系统的UI风格,没什么不同的.然而,在我混合使用这三个手机系统之后,才明白,一个手机系统远不只一个UI那么简单,而真的是可以称之为一个“生态”. 首先祭出三台经典设备 ...
- 搜狗输入法wp风格皮肤
换了个nexus 发现输入法真的没有wp的好用 没办法,刚好搜狗输入法有定制皮肤的选项,所以自己做了个wp风格的输入法皮肤. 一点微小的工作 http://pan.baidu.com/s/1kVsHd ...
- 免费获取WP之类的开发者权限或免费使用Azure 2015-10-19
上一次弄wp真机调试的时候,卡住了,这里讲一下怎么解决(http://www.cnblogs.com/dunitian/p/4870959.html) 进这个网址注册一下:https://www.dr ...
- 【WP开发】读写剪贴板
在WP 8.1中只有Silverlight App支持操作剪贴板的API,Runtime App并不支持.不过,在WP 10中也引入了可以操作剪贴板的API. 顺便说点题外话,有人会说,我8.1的开发 ...
- 【WP开发】不同客户端之间传输加密数据
在上一篇文章中,曾说好本次将提供一个客户端之间传输加密数据的例子.前些天就打算写了,只是因一些人类科技无法预知的事情发生,故拖到今天. 本示例没什么技术含量,也没什么亮点,Bug林立,只不过提供给有需 ...
- 【WP开发】加密篇:双向加密
说起双向加密,如果以前在.NET开发中弄过加/解密的朋友都不会陌生,常用的算法有DES.AES等.在RT应用程序中,也提供了加密相关的API,算法自然是一样的,只是API的封装方式不同罢了,因为RT不 ...
- 【WP 8.1开发】How to 图像处理
在今天的吹牛节目开始之前,先交代一件事: 关于玩WP 8.1开发所使用的VS版本问题.对版本的要求是2013的Update2,这是最低要求,只要是这个版本或以上都可以,而update3,update4 ...
随机推荐
- 【javascript】chormeV8源码阅读之 GC(垃圾回收)过程 笔记
1.为何需要垃圾回收 在V8引擎逐行执行JavaScript代码的过程中,当遇到函数的情况时,会为其创建一个函数执行上下文(Context)环境并添加到调用堆栈的栈顶,函数的作用域(handl ...
- 全新TI AM62xx系列核心板上市,小小身板蕴藏巨大势能!
2011年TI推出AM335x,成为了此后市场上最受欢迎的通用工业级ARM处理器,并广泛应用于工业HMI, 医疗电子,机器人,能源,汽车等领域.随着工业4.0的发展,HMI人机交互.工业工控.医疗等领 ...
- 《Zookeeper分布式过程协同技术详解》之简介-分布式与Zookeeper简介
[常见的分布式架构场景面临的问题]一般在主从架构中,主节点进程负责跟踪从节点的状态和任务的有效性,并分配任务到从节点.而这种架构中必须要解决的几个问题是,主节点崩溃.从节点崩溃.通信故障.主节点崩溃: ...
- SpringBoot笔记--自动配置(高级内容)(下集)
案例需求 实现步骤: 具体的实现 1.引入Jedis依赖 2.提供Jedis的Bean 找到SpringBoot的执行文件,按住Ctrl键,进入SpringBootApplication注解,再进入E ...
- mysql基础知识&&常用命令
了解 什么是数据库?什么是数据管理系统?什么是SQL,他们之间的关系又是什么? 数据库 英文单词DataBase,简称DB,按照一定格式存储数据的一些文件的组合. 顾名思义:存储数据的仓库,实际上就是 ...
- Linux & 标准C语言学习 <DAY9_2>
一.进程映像 程序:存储在磁盘上的可执行文件(二进制文件.脚本文件) 进程:正在系统中运行的程序 进程映像:进程的内存分布情况 text(代码段): ...
- IntelliJ IDEA 下载安装及配置使用教程(图文步骤详解)
前言 壹哥在前面的文章中,带大家下载.安装.配置了Eclipse这个更好用的IDE开发工具,并教会了大家如何在Eclipse中进行项目的创建和代码编写.运行.但是实际上,在各种IDE开发工具中,Ecl ...
- 任意Exe转ShellCode?
之前写过一个远控,但一直在琢磨如何生成shellcode,今天偶然看见一个项目:sRDI,github上就有 这个项目主要就是将dll转成shellcode,于是我就想到了"写一个输出文件的 ...
- Python之进程管理
使用python创建进程 from multiprocessing import Process # 导入进程模块 import time # 定义一个函数,测试创建进程使用 def task(nam ...
- Mybatis中批量插入和一些问题的解决
批量插入有三个问题,第一是执行效率,第二数据冲突,第三数据重跑更新操作. 一般对于这样的问题有以下操作方法. 第一是执行效率:mybatis支持两种高效插入. 1.mybtis的foreach标签,f ...
