深度神经网络（DNN）损失函数和激活函数的选择

　　　　在深度神经网络（DNN）反向传播算法(BP)中，我们对DNN的前向反向传播算法的使用做了总结。里面使用的损失函数是均方差，而激活函数是Sigmoid。实际上DNN可以使用的损失函数和激活函数不少。这些损失函数和激活函数如何选择呢？下面我们就对DNN损失函数和激活函数的选择做一个总结。

1. 均方差损失函数+Sigmoid激活函数的问题

　　　　在讲反向传播算法时，我们用均方差损失函数和Sigmoid激活函数做了实例，首先我们就来看看均方差+Sigmoid的组合有什么问题。

　　　　首先我们回顾下Sigmoid激活函数的表达式为：$$\sigma(z) = \frac{1}{1+e^{-z}}$$

　　　　$\sigma(z)$的函数图像如下：

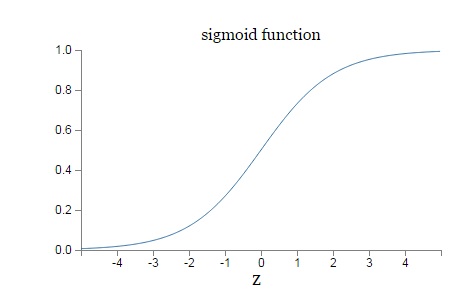
　　　　从图上可以看出，对于Sigmoid，当$z$的取值越来越大后，函数曲线变得越来越平缓，意味着此时的导数$\sigma ^{'}(z)$也越来越小。同样的，当$z$的取值越来越小时，也有这个问题。仅仅在$z$取值为0附近时，导数$\sigma ^{'}(z)$的取值较大。

　　　　在上篇讲的均方差+Sigmoid的反向传播算法中，每一层向前递推都要乘以$\sigma ^{'}(z)$,得到梯度变化值。Sigmoid的这个曲线意味着在大多数时候，我们的梯度变化值很小，导致我们的$W,b$更新到极值的速度较慢，也就是我们的算法收敛速度较慢。那么有什么什么办法可以改进呢？

2. 使用交叉熵损失函数+Sigmoid激活函数改进DNN算法收敛速度

　　　　上一节我们讲到Sigmoid的函数特性导致反向传播算法收敛速度慢的问题，那么如何改进呢？换掉Sigmoid？这当然是一种选择。另一种常见的选择是用交叉熵损失函数来代替均方差损失函数。

　　　　我们来看看每个样本的交叉熵损失函数的形式：$$J(W,b,a,y) = -y \bullet lna- (1-y) \bullet ln(1 -a)$$

　　　　其中，$\bullet$为向量内积。这个形式其实很熟悉，在逻辑回归原理小结中其实我们就用到了类似的形式，只是当时我们是用最大似然估计推导出来的，而这个损失函数的学名叫交叉熵。

　　　　使用了交叉熵损失函数，就能解决Sigmoid函数导数变化大多数时候反向传播算法慢的问题吗？我们来看看当使用交叉熵时，我们各层$\delta^l$的梯度情况。

$$ \begin{align} \delta^l  & = \frac{\partial J(W,b,a^l,y)}{\partial z^l} \\& = -y\frac{1}{a^l}(a^l)(1-a^l) + (1-y) \frac{1}{1-a^l}(a^l)(1-a^l) \\& = -y(1-a^l) -(1-y)a^l \\& = a^l-y \end{align}$$

　　　　可见此时我们的$\delta^l$梯度表达式里面已经没有了$\sigma ^{'}(z)$，作为一个特例，回顾一下我们上一节均方差损失函数时在$\delta^L$梯度，$$\frac{\partial J(W,b,x,y)}{\partial z^L} = (a^L-y) \odot \sigma^{'}(z)$$

　　　　对比两者在第L层的$\delta^L$梯度表达式，就可以看出，使用交叉熵，得到的的$\delta^l$梯度表达式没有了$\sigma^{'}(z)$，梯度为预测值和真实值的差距，这样求得的$W^l,b^l$的地图也不包含$\sigma^{'}(z)$，因此避免了反向传播收敛速度慢的问题。

　　　　通常情况下，如果我们使用了sigmoid激活函数，交叉熵损失函数肯定比均方差损失函数好用。

3. 使用对数似然损失函数和softmax激活函数进行DNN分类输出

　　　　在前面我们讲的所有DNN相关知识中，我们都假设输出是连续可导的值。但是如果是分类问题，那么输出是一个个的类别，那我们怎么用DNN来解决这个问题呢？

　　　　比如假设我们有一个三个类别的分类问题，这样我们的DNN输出层应该有三个神经元，假设第一个神经元对应类别一，第二个对应类别二，第三个对应类别三，这样我们期望的输出应该是(1,0,0)，（0,1,0）和(0,0,1)这三种。即样本真实类别对应的神经元输出应该无限接近或者等于1，而非改样本真实输出对应的神经元的输出应该无限接近或者等于0。或者说，我们希望输出层的神经元对应的输出是若干个概率值，这若干个概率值即我们DNN模型对于输入值对于各类别的输出预测，同时为满足概率模型，这若干个概率值之和应该等于1。

　　　　DNN分类模型要求是输出层神经元输出的值在0到1之间，同时所有输出值之和为1。很明显，现有的普通DNN是无法满足这个要求的。但是我们只需要对现有的全连接DNN稍作改良，即可用于解决分类问题。在现有的DNN模型中，我们可以将输出层第i个神经元的激活函数定义为如下形式：$$a_i^L = \frac{e^{z_i^L}}{\sum\limits_{j=1}^{n_L}e^{z_j^L}}$$

　　　　其中，$n_L$是输出层第L层的神经元个数，或者说我们的分类问题的类别数。

　　　　很容易看出，所有的$a_i^L$都是在(0,1) 之间的数字，而$\sum\limits_{j=1}^{n_L}e^{z_j^L}$作为归一化因子保证了所有的$a_i^L$之和为1。

　　　　这个方法很简洁漂亮，仅仅只需要将输出层的激活函数从Sigmoid之类的函数转变为上式的激活函数即可。上式这个激活函数就是我们的softmax激活函数。它在分类问题中有广泛的应用。将DNN用于分类问题，在输出层用softmax激活函数也是最常见的了。

　　　　下面这个例子清晰的描述了softmax激活函数在前向传播算法时的使用。假设我们的输出层为三个神经元，而未激活的输出为3,1和-3，我们求出各自的指数表达式为：20,2.7和0.05，我们的归一化因子即为22.75，这样我们就求出了三个类别的概率输出分布为0.88，0.12和0。

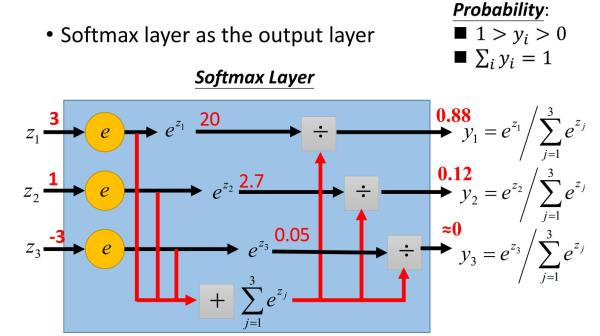
　　　　从上面可以看出，将softmax用于前向传播算法是也很简单的。那么在反向传播算法时还简单吗？反向传播的梯度好计算吗？答案是Yes！

　　　　对于用于分类的softmax激活函数，对应的损失函数一般都是用对数似然函数，即：$$J(W,b,a^L,y) = - \sum\limits_ky_klna_k^L$$

　　　　其中$y_k$的取值为0或者1，如果某一训练样本的输出为第i类。则$y_i=1$,其余的$j \neq i$都有$y_j=0$。由于每个样本只属于一个类别，所以这个对数似然函数可以简化为：$$J(W,b,a^L,y) = -lna_i^L$$

　　　　其中$i$即为训练样本真实的类别序号。

　　　　可见损失函数只和真实类别对应的输出有关，这样假设真实类别是第i类，则其他不属于第i类序号对应的神经元的梯度导数直接为0。对于真实类别第i类，它的$W_i^L$对应的梯度计算为：$$ \begin{align} \frac{\partial J(W,b,a^L,y)}{\partial W_i^L}& = \frac{\partial J(W,b,a^L,y)}{\partial a_i^L}\frac{\partial a_i^L}{\partial z_i^L}\frac{\partial z_i^L}{\partial w_i^L} \\& = -\frac{1}{a_i^L}\frac{(e^{z_i^L})\sum\limits_{j=1}^{n_L}e^{z_j^L}-e^{z_i^L}e^{z_i^L}}{(\sum\limits_{j=1}^{n_L}e^{z_j^L)^2}} a_i^{L-1} \\& = -\frac{1}{a_i^L} (\frac{e^{z_i^L}}{\sum\limits_{j=1}^{n_L}e^{z_j^L}}-\frac{e^{z_i^L}}{\sum\limits_{j=1}^{n_L}e^{z_j^L}}\frac{e^{z_i^L}}{\sum\limits_{j=1}^{n_L}e^{z_j^L}}) a_i^{L-1} \\& = -\frac{1}{a_i^L} a_i^L(1- a_i^L) a_i^{L-1} \\& = (a_i^L -1)  a_i^{L-1} \end{align}$$

　　　　同样的可以得到$b_i^L$的梯度表达式为：$$\frac{\partial J(W,b,a^L,y)}{\partial b_i^L} = a_i^L -1$$

　　　　可见，梯度计算也很简洁，也没有第一节说的训练速度慢的问题。举个例子，假如我们对于第2类的训练样本，通过前向算法计算的为激活输出为（1,5,3），则我们得到softmax激活后的概率输出为：(0.015,0.866,0.117)。由于我们的类别是第二类，则反向传播的梯度应该为：(0.015,0.866-1,0.117)。是不是很简单呢？

　　　　当softmax输出层的反向传播计算完以后，后面的普通DNN层的反向传播计算和之前讲的普通DNN没有区别。　

4. 梯度爆炸梯度消失与ReLU激活函数

　　　　学习DNN，大家一定听说过梯度爆炸和梯度消失两个词。尤其是梯度消失，是限制DNN与深度学习的一个关键障碍，目前也没有完全攻克。

　　　　什么是梯度爆炸和梯度消失呢？从理论上说都可以写一篇论文出来。不过简单理解，就是在反向传播的算法过程中，由于我们使用了是矩阵求导的链式法则，有一大串连乘，如果连乘的数字在每层都是小于1的，则梯度越往前乘越小，导致梯度消失，而如果连乘的数字在每层都是大于1的，则梯度越往前乘越大，导致梯度爆炸。

　　　　比如我们在前一篇反向传播算法里面讲到了$\delta$的计算，可以表示为：$$\delta^l =\frac{\partial J(W,b,x,y)}{\partial z^l} = \frac{\partial J(W,b,x,y)}{\partial z^L}\frac{\partial z^L}{\partial z^{L-1}}\frac{\partial z^{L-1}}{\partial z^{L-2}}...\frac{\partial z^{l+1}}{\partial z^{l}}$$

　　　　如果不巧我们的样本导致每一层$\frac{\partial z^{l+1}}{\partial z^{l}}$的都小于1，则随着反向传播算法的进行，我们的$\delta^l$会随着层数越来越小，甚至接近越0，导致梯度几乎消失，进而导致前面的隐藏层的$W,b$参数随着迭代的进行，几乎没有大的改变，更谈不上收敛了。这个问题目前没有完美的解决办法。

　　　　而对于梯度爆炸，则一般可以通过调整我们DNN模型中的初始化参数得以解决。

　　　　对于无法完美解决的梯度消失问题，目前有很多研究，一个可能部分解决梯度消失问题的办法是使用ReLU（Rectified Linear Unit）激活函数，ReLU在卷积神经网络CNN中得到了广泛的应用，在CNN中梯度消失似乎不再是问题。那么它是什么样子呢？其实很简单，比我们前面提到的所有激活函数都简单，表达式为：$$\sigma(z) = max(0,z)$$

　　　　也就是说大于等于0则不变，小于0则激活后为0。就这么一玩意就可以解决梯度消失？至少部分是的。具体的原因现在其实也没有从理论上得以证明。这里我也就不多说了。

5. DNN其他激活函数

　　　　除了上面提到了激活函数，DNN常用的激活函数还有：

　　　　1） tanh：这个是sigmoid的变种，表达式为：$$tanh(z) = \frac{e^z-e^{-z}}{e^z+e^{-z}}$$

　　　　tanh激活函数和sigmoid激活函数的关系为：$$tanh(z) = 2sigmoid(2z)-1$$

　　　　tanh和sigmoid对比主要的特点是它的输出落在了[-1,1],这样输出可以进行标准化。同时tanh的曲线在较大时变得平坦的幅度没有sigmoid那么大，这样求梯度变化值有一些优势。当然，要说tanh一定比sigmoid好倒不一定，还是要具体问题具体分析。

　　　　2） softplus：这个其实就是sigmoid函数的原函数，表达式为：$$softplus(z) = log(1+e^z)$$

　　　　它的导数就是sigmoid函数。softplus的函数图像和ReLU有些类似。它出现的比ReLU早，可以视为ReLU的鼻祖。

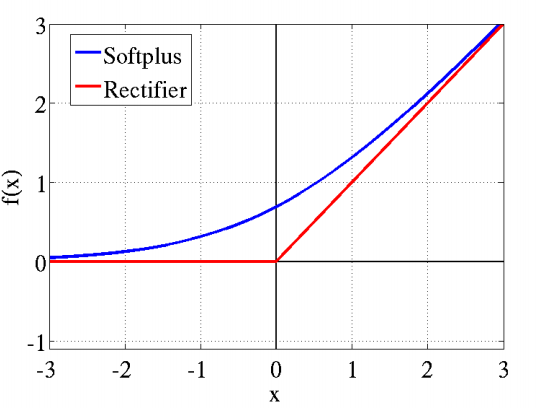
　　　　3）PReLU：从名字就可以看出它是ReLU的变种，特点是如果未激活值小于0，不是简单粗暴的直接变为0，而是进行一定幅度的缩小。如下图。当然，由于ReLU的成功，有很多的跟风者，有其他各种变种ReLU，这里就不多提了。

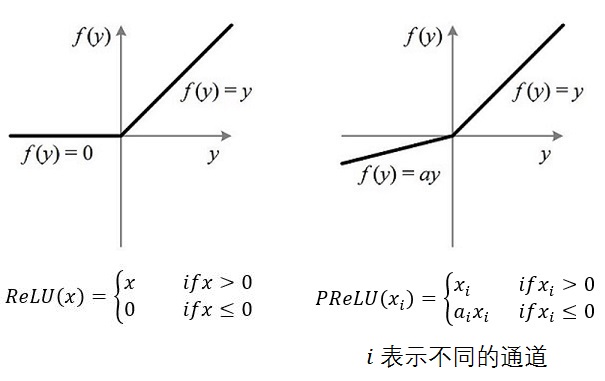
6. DNN损失函数和激活函数小结

　　　　上面我们对DNN损失函数和激活函数做了详细的讨论，重要的点有：1）如果使用sigmoid激活函数，则交叉熵损失函数一般肯定比均方差损失函数好。2）如果是DNN用于分类，则一般在输出层使用softmax激活函数和对数似然损失函数。3）ReLU激活函数对梯度消失问题有一定程度的解决，尤其是在CNN模型中。

　　　　下一篇我们讨论下DNN模型的正则化问题。

（欢迎转载，转载请注明出处。欢迎沟通交流： pinard.liu@ericsson.com）

参考资料：

1） Neural Networks and Deep Learning by By Michael Nielsen

2） Deep Learning, book by Ian Goodfellow, Yoshua Bengio, and Aaron Courville

3） UFLDL Tutorial