WPF命中测试示例(二)——几何区域命中测试

原文:WPF命中测试示例(二)——几何区域命中测试

接续上次的命中测试，这次来做几何区域测试示例。

示例

首先新建一个WPF项目，在主界面中拖入一个按钮控件，并修改代码中的以下高亮位置：

当前设计视图界面如下：

接下来，转到窗体的“Window_Loaded”事件处理函数，编写函数代码：

private void Window_Loaded(object sender, RoutedEventArgs e)
{
Random r = new Random();
for (int i = 0; i < 800; i++)
{
var o = new Ellipse();
o.HorizontalAlignment = HorizontalAlignment.Left;
o.VerticalAlignment = VerticalAlignment.Top;
o.Margin=new Thickness(){ Left = r.Next((int)this.Width),Top = r.Next((int)this.Height)};
o.Height = o.Width = r.Next(10);
o.Fill = new SolidColorBrush(new Color() { A = (byte)r.Next(255), R = (byte)r.Next(255), G = (byte)r.Next(255), B = (byte)r.Next(255) });
root.Children.Add(o);
}
}

代码的功能是在界面中随机分布800个不同色彩的小圆点，我们来编译运行看看效果：

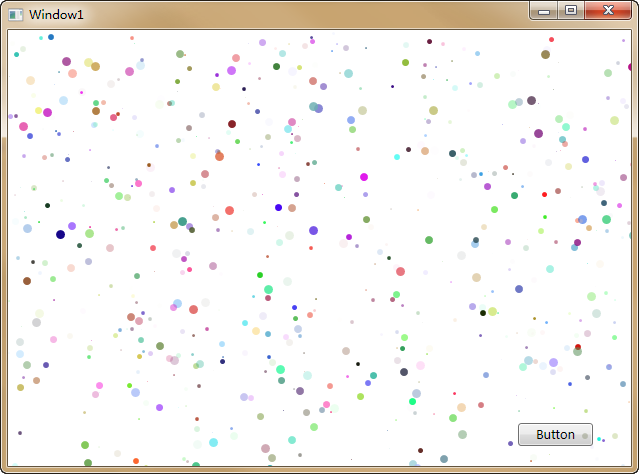
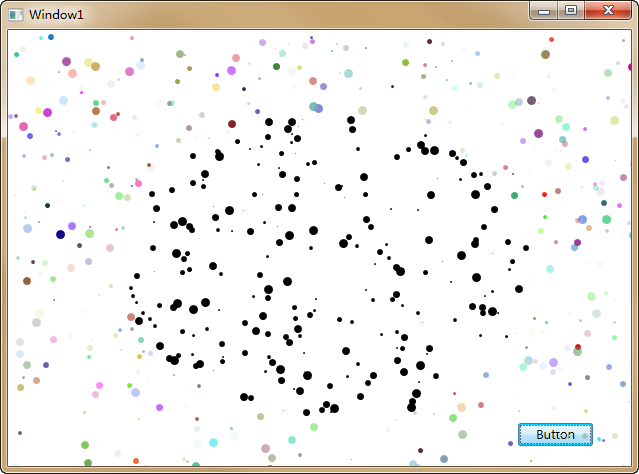
现在，我们需要在按钮点击时，将中间200×150椭圆区域内的小圆点变成黑色。

编写按钮点击事件处理函数如下：

private void button1_Click(object sender, RoutedEventArgs e)
{
VisualTreeHelper.HitTest(root, null, f =>
{
var o = f.VisualHit as Ellipse;
if (o != null) o.Fill = new SolidColorBrush(Color.FromArgb(255, 0, 0, 0));
return HitTestResultBehavior.Continue;
}, new GeometryHitTestParameters(new EllipseGeometry(new Point(this.Width / 2, this.Height / 2), 200, 150)));
}

这里的HitTestParameters就采用了GeometryHitTestParameters，传入一个几何图形作为命中测试区域。

编译运行效果：

下载

源代码：http://www.uushare.com/user/icesee/file/3024856

本文的XPS版本：http://www.uushare.com/user/icesee/file/3024874