OpenACC 绘制曼德勃罗集
▶ 书上第四章,用一系列步骤优化曼德勃罗集的计算过程。
● 代码
// constants.h
const unsigned int WIDTH=;
const unsigned int HEIGHT=;
const unsigned int MAX_ITERS=;
const unsigned int MAX_COLOR=;
const double xmin=-1.7;
const double xmax=.;
const double ymin=-1.2;
const double ymax=1.2;
const double dx = (xmax - xmin) / WIDTH;
const double dy = (ymax - ymin) / HEIGHT;
// mandelbrot.h
#pragma acc routine seq
unsigned char mandelbrot(int Px, int Py);
// mandelbrot.cpp
#include <cstdio>
#include <cstdlib>
#include <fstream>
#include "mandelbrot.h"
#include "constants.h" using namespace std; unsigned char mandelbrot(int Px, int Py)
{
const double x0 = xmin + Px * dx, y0 = ymin + Py * dy;
double x = 0.0, y = 0.0;
int i;
for(i=; x * x + y * y < 4.0 && i < MAX_ITERS; i++)
{
double xtemp = x * x - y * y + x0;
y = * x * y + y0;
x = xtemp;
}
return (double)MAX_COLOR * i / MAX_ITERS;
}
// main.cpp
#include <cstdio>
#include <cstdlib>
#include <fstream>
#include <cstring>
#include <omp.h>
#include <openacc.h> #include "mandelbrot.h"
#include "constants.h" using namespace std; int main()
{
unsigned char *image = (unsigned char*)malloc(sizeof(unsigned int) * WIDTH * HEIGHT);
FILE *fp=fopen("image.pgm","wb");
fprintf(fp,"P5\n\"#comment\"\n%d %d\n%d\n",WIDTH, HEIGHT, MAX_COLOR); acc_init(acc_device_nvidia);
#pragma acc parallel num_gangs(1)
{
image[] = ;
}
double st = omp_get_wtime();
#pragma acc parallel loop
for(int y = ; y < HEIGHT; y++)
{
for(int x = ; x < WIDTH; x++)
image[y * WIDTH + x] = mandelbrot(x, y);
}
double et = omp_get_wtime();
printf("Time: %lf seconds.\n", (et-st));
fwrite(image,sizeof(unsigned char),WIDTH * HEIGHT, fp);
fclose(fp);
free(image);
return ;
}
● 输出结果
// Ubuntu:
cuan@CUAN:/media/cuan/02FCDA52FCDA4019/Code/ParallelProgrammingWithOpenACC-master/Chapter04/cpp$ pgc++ -std=c++ -acc -mp -fast -Minfo -c mandelbrot.cpp
mandelbrot(int, int):
, Generating acc routine seq
Generating Tesla code
, FMA (fused multiply-add) instruction(s) generated
, Loop not vectorized/parallelized: potential early exits
, FMA (fused multiply-add) instruction(s) generated
cuan@CUAN:/media/cuan/02FCDA52FCDA4019/Code/ParallelProgrammingWithOpenACC-master/Chapter04/cpp$ pgc++ -std=c++ -acc -mp -fast -Minfo main.cpp mandelbrot.o -o acc1.exe
main.cpp:
main:
, Accelerator kernel generated
Generating Tesla code
Generating implicit copyout(image[])
, Accelerator kernel generated
Generating Tesla code
, #pragma acc loop gang /* blockIdx.x */
, #pragma acc loop vector(128) /* threadIdx.x */
, Generating implicit copy(image[:])
, Loop is parallelizable
Loop not vectorized/parallelized: contains call
cuan@CUAN:/media/cuan/02FCDA52FCDA4019/Code/ParallelProgrammingWithOpenACC-master/Chapter04/cpp$ ./acc1.exe
Time: 0.646578 seconds.
● 优化 03,变化仅在 main.cpp 中
// main.cpp
#include <cstdio>
#include <cstdlib>
#include <fstream>
#include <cstring>
#include <omp.h>
#include <openacc.h>
#include "mandelbrot.h"
#include "constants.h" using namespace std; int main()
{
const int num_blocks = , block_size = HEIGHT / num_blocks * WIDTH;
unsigned char *image=(unsigned char*)malloc(sizeof(unsigned int) * WIDTH * HEIGHT);
FILE *fp=fopen("image.pgm","wb");
fprintf(fp,"P5\n\"#comment\"\n%d %d\n%d\n",WIDTH, HEIGHT, MAX_COLOR); acc_init(acc_device_nvidia);
#pragma acc parallel num_gangs(1)
{
image[] = ;
}
double st = omp_get_wtime();
#pragma acc data create(image[WIDTH*HEIGHT])
{
for(int block = ; block < num_blocks; block++)
{
const int start = block * (HEIGHT/num_blocks), end = start + (HEIGHT/num_blocks);
#pragma acc parallel loop async(block)
for(int y=start;y<end;y++)
{
for(int x=;x<WIDTH;x++)
image[y*WIDTH+x]=mandelbrot(x,y);
}
#pragma acc update self(image[block*block_size:block_size]) async(block)
}
}
#pragma acc wait double et = omp_get_wtime();
printf("Time: %lf seconds.\n", (et-st));
fwrite(image,sizeof(unsigned char), WIDTH * HEIGHT, fp);
fclose(fp);
free(image);
return ;
}
● 输出结果
// Ubuntu:
cuan@CUAN:/media/cuan/02FCDA52FCDA4019/Code/ParallelProgrammingWithOpenACC-master/Chapter04/cpp/task3$ pgc++ -std=c++ -acc -mp -fast -Minfo -c mandelbrot.cpp
mandelbrot(int, int):
, Generating acc routine seq
Generating Tesla code
, FMA (fused multiply-add) instruction(s) generated
, Loop not vectorized/parallelized: potential early exits
, FMA (fused multiply-add) instruction(s) generated
cuan@CUAN:/media/cuan/02FCDA52FCDA4019/Code/ParallelProgrammingWithOpenACC-master/Chapter04/cpp/task3$ pgc++ -std=c++ -acc -mp -fast -Minfo main.cpp mandelbrot.o -o acc2.exe
main.cpp:
main:
, Accelerator kernel generated
Generating Tesla code
Generating implicit copyout(image[])
, Generating create(image[:])
, Accelerator kernel generated
Generating Tesla code
, #pragma acc loop gang /* blockIdx.x */
, #pragma acc loop vector(128) /* threadIdx.x */
, Loop is parallelizable
Loop not vectorized/parallelized: contains call
, Generating update self(image[block*:])
cuan@CUAN:/media/cuan/02FCDA52FCDA4019/Code/ParallelProgrammingWithOpenACC-master/Chapter04/cpp/task3$ ./acc2.exe
Time: 0.577263 seconds.
● 优化 05,添加异步计算
// main.cpp
#include <cstdio>
#include <cstdlib>
#include <fstream>
#include <cstring>
#include <omp.h>
#include <openacc.h>
#include "mandelbrot.h"
#include "constants.h" using namespace std; int main()
{
const int num_blocks=, block_size = HEIGHT / num_blocks * WIDTH;
unsigned char *image=(unsigned char*)malloc(sizeof(unsigned int) * WIDTH * HEIGHT);
FILE *fp = fopen("image.pgm", "wb");
fprintf(fp,"P5\n\"#comment\"\n%d %d\n%d\n",WIDTH, HEIGHT, MAX_COLOR); const int num_gpus = acc_get_num_devices(acc_device_nvidia); #pragma omp parallel num_threads(num_gpus)
{
acc_init(acc_device_nvidia);
acc_set_device_num(omp_get_thread_num(),acc_device_nvidia);
}
printf("Found %d NVIDIA GPUs.\n", num_gpus); double st = omp_get_wtime();
#pragma omp parallel num_threads(num_gpus)
{
int queue = ;
int my_gpu = omp_get_thread_num();
acc_set_device_num(my_gpu,acc_device_nvidia);
printf("Thread %d is using GPU %d\n", my_gpu, acc_get_device_num(acc_device_nvidia));
#pragma acc data create(image[WIDTH*HEIGHT])
{
#pragma omp for schedule(static, 1)
for(int block = ; block < num_blocks; block++)
{
const int start = block * (HEIGHT/num_blocks), end = start + (HEIGHT/num_blocks);
#pragma acc parallel loop async(queue)
for(int y=start;y<end;y++)
{
for(int x=;x<WIDTH;x++)
image[y*WIDTH+x]=mandelbrot(x,y);
} #pragma acc update self(image[block*block_size:block_size]) async(queue)
queue = (queue + ) % ;
}
}
#pragma acc wait
} double et = omp_get_wtime();
printf("Time: %lf seconds.\n", (et-st));
fwrite(image,sizeof(unsigned char), WIDTH * HEIGHT, fp);
fclose(fp);
free(image);
return ;
}
● 输出结果
// Ubuntu:
cuan@CUAN:/media/cuan/02FCDA52FCDA4019/Code/ParallelProgrammingWithOpenACC-master/Chapter04/cpp/task5.multithread$ pgc++ -std=c++ -acc -mp -fast -Minfo -c mandelbrot.cpp
mandelbrot(int, int):
, Generating acc routine seq
Generating Tesla code
, FMA (fused multiply-add) instruction(s) generated
, Loop not vectorized/parallelized: potential early exits
, FMA (fused multiply-add) instruction(s) generated
cuan@CUAN:/media/cuan/02FCDA52FCDA4019/Code/ParallelProgrammingWithOpenACC-master/Chapter04/cpp/task5.multithread$ pgc++ -std=c++ -acc -mp -fast -Minfo main.cpp mandelbrot.o -o acc3.exe
main.cpp:
main:
, Parallel region activated
, Parallel region terminated
, Parallel region activated
, Generating create(image[:])
, Parallel loop activated with static cyclic schedule
, Accelerator kernel generated
Generating Tesla code
, #pragma acc loop gang /* blockIdx.x */
, #pragma acc loop vector(128) /* threadIdx.x */
, Loop is parallelizable
Loop not vectorized/parallelized: contains call
, Generating update self(image[block*:])
, Barrier
, Parallel region terminated
cuan@CUAN:/media/cuan/02FCDA52FCDA4019/Code/ParallelProgrammingWithOpenACC-master/Chapter04/cpp/task5.multithread$ ./acc3.exe
Found NVIDIA GPUs.
Thread is using GPU
Time: 0.497450 seconds.
● nvprof 的结果汇总,三张图分别为 “并行和数据优化”,“优化 03(分块分流)” 和 “优化 05(分块调度)”
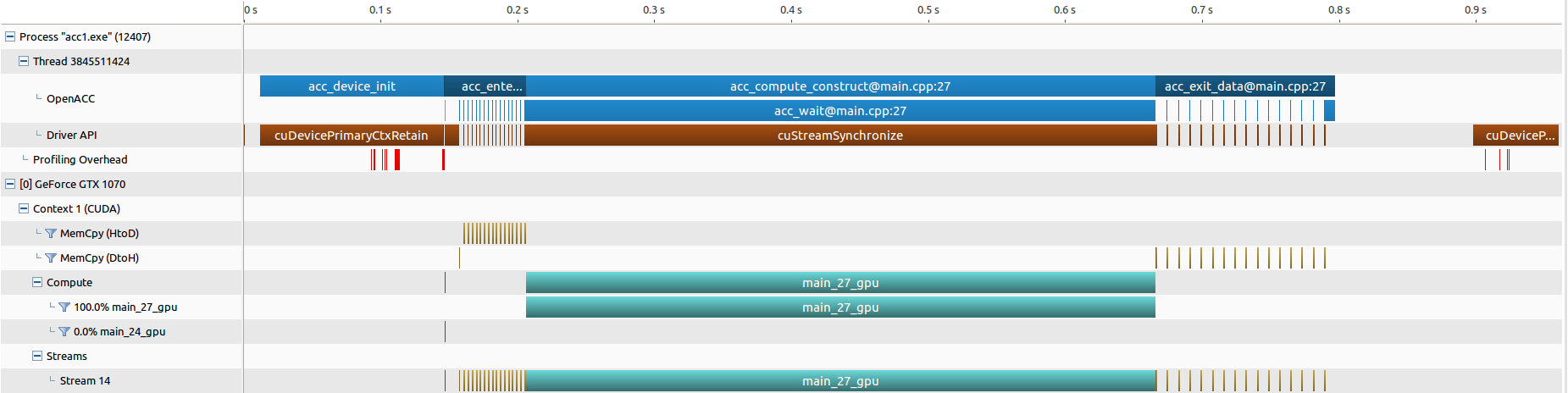
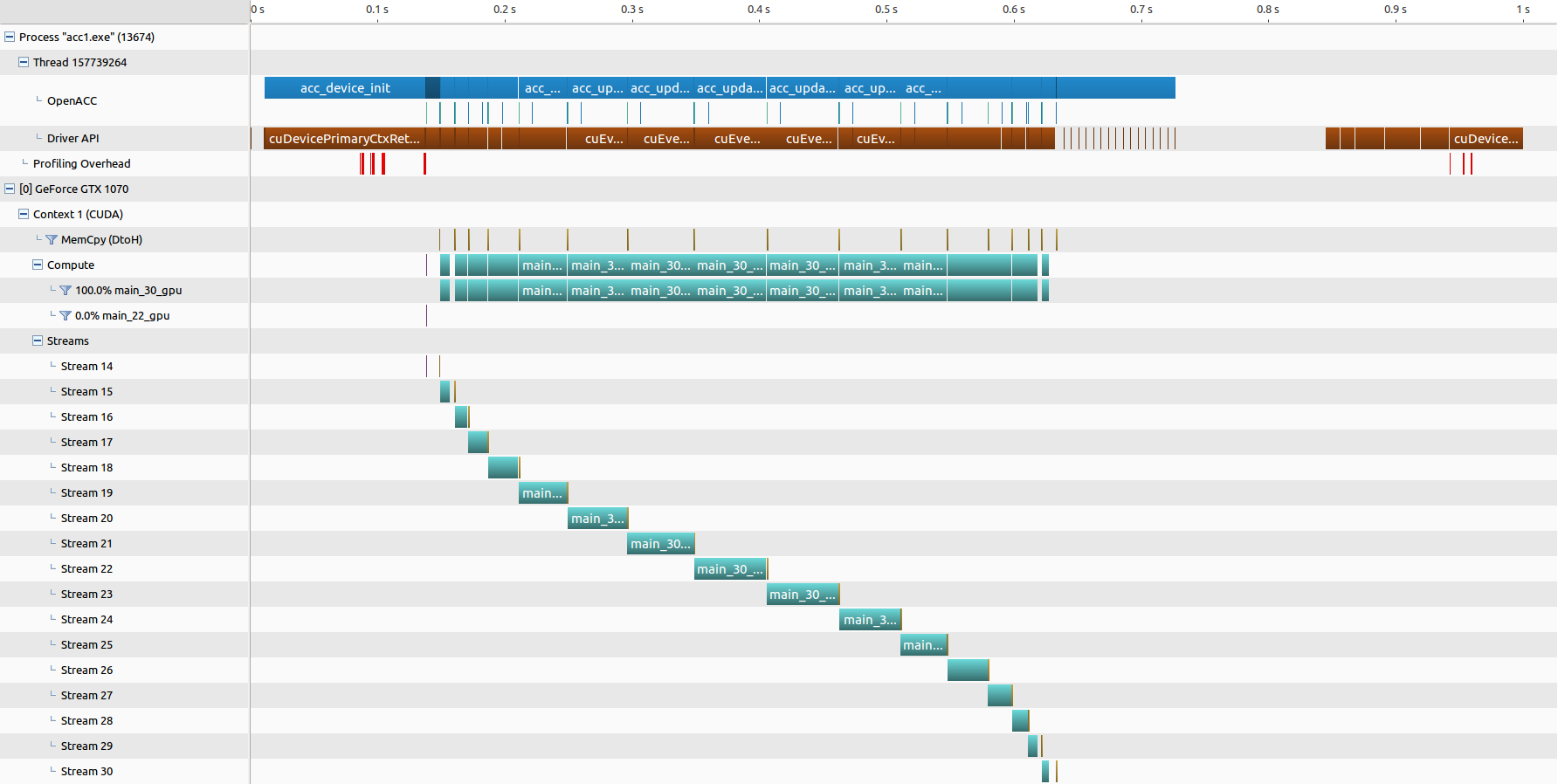
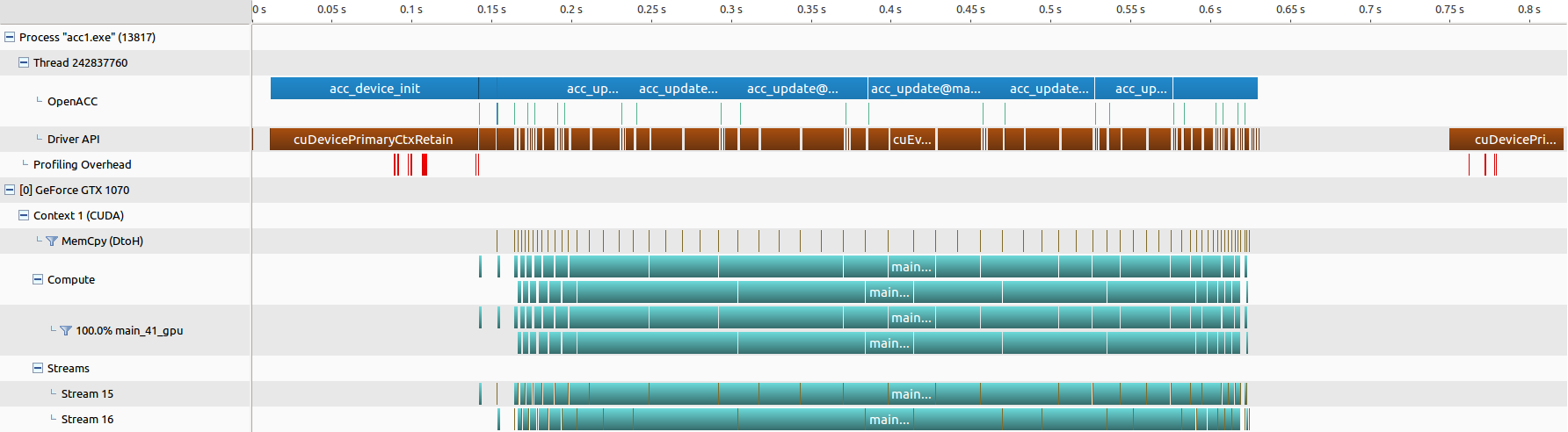
OpenACC 绘制曼德勃罗集的更多相关文章
- 曼德勃罗(Mandelbrot)集合与其编程实现
一.从科赫雪花谈起 设想一个边长为1的等边三角形(例如以下图所看到的).取每边中间的三分之中的一个,接上去一个形状全然类似的但边长为其三分之中的一个的三角形,结果是一个六角形.如今取六角形的每个边做相 ...
- 【C++】Mandelbrot集绘制(生成ppm文件)
曼德勃罗特集是人类有史以来做出的最奇异,最瑰丽的几何图形.曾被称为"上帝的指纹". 这个点集均出自公式:Zn+1=(Zn)^2+C.(此处Z.C均为复数)所有使得该公式无限迭代后的 ...
- python图片和分形树
链接: 这10个Python项目很有趣! Python 绘制分形图(曼德勃罗集.分形树叶.科赫曲线.分形龙.谢尔宾斯基三角等)附代码 使用Python生成树形图案 神奇的代码:用 Python 生成分 ...
- Pollard Rho 算法简介
\(\text{update 2019.8.18}\) 由于本人将大部分精力花在了cnblogs上,而不是洛谷博客,评论区提出的一些问题直到今天才解决. 下面给出的Pollard Rho函数已给出散点 ...
- Miller-Rabin and Pollard-Rho
实话实说,我自学(肝)了两天才学会这两个随机算法 记录: Miller-Rabin 她是一个素数判定的算法. 首先需要知道费马小定理 \[a^{p-1}\equiv1\pmod{p}\quad p\i ...
- 使用OpenGL进行Mandelbrot集的可视化
Mandelbrot集是哪一集?? Mandelbrot集不是哪一集!! 啊不对-- Mandelbrot集是哪一集!! 好像也不对-- Mandelbrot集是数集!! 所以--他不是一集而是数集? ...
- 混沌分形之朱利亚集(JuliaSet)
朱利亚集合是一个在复平面上形成分形的点的集合.以法国数学家加斯顿·朱利亚(Gaston Julia)的名字命名.我想任何一个有关分形的资料都不会放过曼德勃罗集和朱利亚集.这里将以点集的方式生成出朱利亚 ...
- 【机器学习Machine Learning】资料大全
昨天总结了深度学习的资料,今天把机器学习的资料也总结一下(友情提示:有些网站需要"科学上网"^_^) 推荐几本好书: 1.Pattern Recognition and Machi ...
- 机器学习(Machine Learning)&深度学习(Deep Learning)资料【转】
转自:机器学习(Machine Learning)&深度学习(Deep Learning)资料 <Brief History of Machine Learning> 介绍:这是一 ...
随机推荐
- scroll滚动动画(js/ts)
//(蓝色this部分为dom) scrollToLeft(option?: { duration?: number, direction?: number }) { let direction = ...
- ElasticSearch(三):ES单机版本基本操作之删除,修改,插入
1. 创建索引 1.1 直接创建索引 可以直接使用head插件创建索引,指定分片数和备份数即可.如下图: 1.2 创建结构化索引 上图创建的索引,点开索引信息,mapping是空的,表示该索引的字段并 ...
- 树的遍历算法-只有一个变量T-递归和非递归
void PostOrderTraverse(BTNode *T) { //就用到了一个变量T if(T==NULL) return; PostOrderTraverse(T->lchild); ...
- MySQL--查询表统计信息
============================================================= 可以用show table status 来查看表的信息,如:show ta ...
- adnanh webhook 框架execute-command 以及参数传递处理
adnanh webhook是一个很不错的webhook 实现,方便灵活. adnanh webhook 支持以下功能: 接收请求 解析header 以及负载以及查询变量 规则检查 执行命令 下面 ...
- 彻底删除vscode及安装的插件和个人配置信息
1.卸载vscode应用软件(在控制面板里面找不到改软件,所以只能进入应用所在文件夹进行卸载) ## 此步骤虽然删掉了应用软件,但是此时重新安装会发现之前下载的插件和个人配置信息都还会重新加载出来,所 ...
- TensorFlow笔记-06-神经网络优化-损失函数,自定义损失函数,交叉熵
TensorFlow笔记-06-神经网络优化-损失函数,自定义损失函数,交叉熵 神经元模型:用数学公式比表示为:f(Σi xi*wi + b), f为激活函数 神经网络 是以神经元为基本单位构成的 激 ...
- junit 知识点
JUnit 测试框架具有以下重要特性: 测试工具 测试套件 测试运行器 测试分类 测试工具 测试工具是一整套固定的工具用于基线测试.测试工具的目的是为了确保测试能够在共享且固定的环境中运行,因此保证测 ...
- windows 安装操作系统时切换分区表格式
在出现分区管理界面时,按下shift+F10呼出命令行,输入diskpart 后尝试如下命令将磁盘分区表手动转换到MBR. list disk ---- 显示当前磁盘列表 select disk x ...
- php 5.2.17 升级到5.3.29
修改php.ini配置文件 register_globals =On include_path = ".;d:/testoa/webroot" error_reporting = ...
