跟我一起了解koa之koa洋葱圈模型（二）

根据上篇博文的博文，继续接下来我们实现的洋葱圈模型的实现

新建middleware文件夹

//m1.js
function m1(ctx){
    global.console.log('m1')
}
module.exports = function(){
    return async function(ctx,next){
        global.console.log('m1 start')
        m1(ctx)
        await next()
        global.console.log('m1 end')
    }
}

//m2.js
function m3(ctx){
    global.console.log('m3')
}
module.exports = function(){
    return async function(ctx,next){
        global.console.log('m3 start')
        m3(ctx)
        await next()
        global.console.log('m3 end')
    }
}

//m3.js
function m2(ctx){
    global.console.log('m2')
}
module.exports = function(){
    return async function(ctx,next){
        global.console.log('m2 start')
        m2(ctx)
        await next()
        global.console.log('m2 end')
    }
}

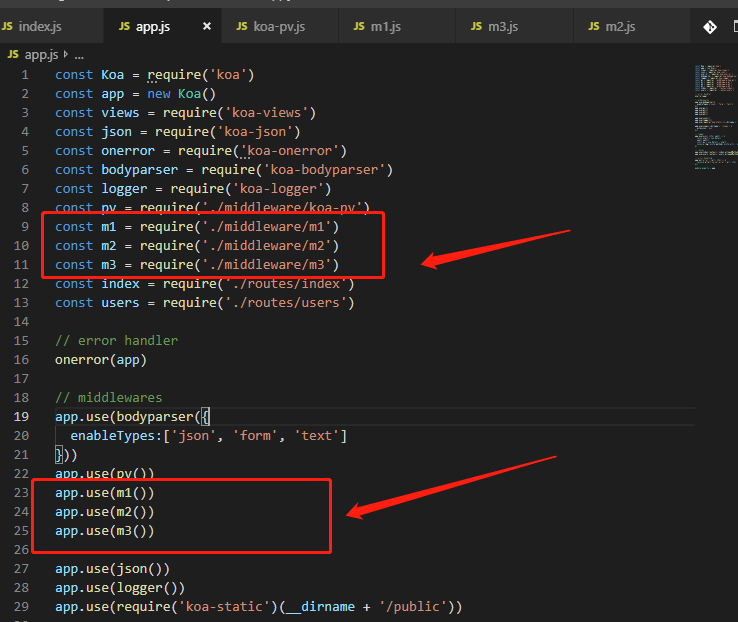
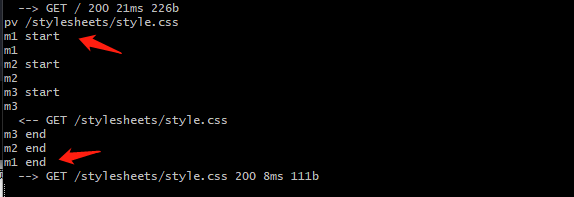
运行结果为