「洛谷P1402」酒店之王 解题报告

P1402 酒店之王

题目描述

XX酒店的老板想成为酒店之王，本着这种希望，第一步要将酒店变得人性化。由于很多来住店的旅客有自己喜好的房间色调、阳光等，也有自己所爱的菜，但是该酒店只有p间房间，一天只有固定的q道不同的菜。

有一天来了n个客人，每个客人说出了自己喜欢哪些房间，喜欢哪道菜。但是很不幸，可能做不到让所有顾客满意（满意的条件是住进喜欢的房间，吃到喜欢的菜）。

这里要怎么分配，能使最多顾客满意呢？

输入输出格式

输入格式：

第一行给出三个正整数表示n,p,q(<=100)。

之后n行，每行p个数包含0或1，第i个数表示喜不喜欢第i个房间（1表示喜欢，0表示不喜欢）。

之后n行，每行q个数，表示喜不喜欢第i道菜。

输出格式：

最大的顾客满意数。

输入输出样例

输入样例#1：

2 2 2
1 0
1 0
1 1
1 1

输出样例#1：

1

---

算法

网络最大流。这里不详细讲，请大家先掌握。

思路

注意，以下出现的所有边边权皆为1，且其反向边边权为0

我们以房间、菜、人为点建图。

像这样：

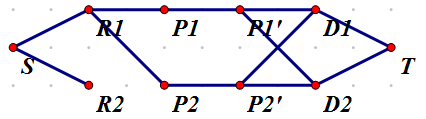
S(=0)表示额外建的一个起始点，Ri(=i + n + n)表示第i个房间，Di(=i+n+n+p)表示第i种菜，由于人只有一个，而网络流处理只经过一个点不方便，我们采用一种神奇方法——拆点！也就是说，把一个人看做两个点，要匹配这个人必须经过这个人两点之间的边，这样就可以控制这个人只匹配一次。如图，Pi(=i)、Pi'(=i+n)表示第i个人。

然后建边。如图，将S与所有Ri相连，将所有的Di与T相连，S作为源点，T作为汇点。如果Pi喜欢Rj，就将Pi与Rj相连。如果Pi喜欢Dj，就将Dj与Pi'之间相连。当然，Pi与Pi'之间也要连一条边。

然后就可以套网络最大流辣。最后得出的答案即为满意数。

拓展

有一天来了n批客人，每批客人喜欢的菜、房间都相同。第i批客人有gi位客人。其余同原题。

HINT:我们可以把每批客人当做2个点Pi、Pi'，在Pi、Pi'之间连gi条边连一条权为gi的边即可。菜、房间每种有多个同理。

代码

#include<bits/stdc++.h>
using namespace std;
#define open(s) freopen( s".in", "r", stdin ), freopen( s".out", "w", stdout )
#define MAXN 405
#define MAXM 40005

int n, p, q;
int hd[MAXN], nxt[MAXM << 1], to[MAXM << 1], val[MAXM << 1], tot(1);
int ans, dis[MAXN];
queue<int> Q;

int x, y;
int S, T;

void Add( int x, int y, int z ){ nxt[++tot] = hd[x]; hd[x] = tot; to[tot] = y; val[tot] = z; }

bool BFS(){
	while( !Q.empty() ) Q.pop();
	memset( dis, 0, sizeof dis );
	Q.push(S); dis[S] = 1;
	while( !Q.empty() ){
		x = Q.front(); Q.pop();
		for ( int i = hd[x]; i; i = nxt[i] )
			if ( val[i] && !dis[to[i]] ){
				dis[to[i]] = dis[x] + 1;
				Q.push( to[i] );
				if ( to[i] == T ) return 1;
			}
	}
	return 0;
}

int DFS( int x, int fl ){
	if ( x == T ) return fl;
	int res(fl), k;
	for ( int i = hd[x]; i && res; i = nxt[i] ){
		if ( val[i] && dis[to[i]] == dis[x] + 1 ){
			k = DFS( to[i], min( res, val[i] ) );
			if ( !k ) dis[to[i]] = 0;
			val[i] -= k; val[i^1] += k; res -= k;
		}
	}
	return fl - res;
}

int main(){
	scanf( "%d%d%d", &n, &p, &q );
	S = 0; T = 1 + n + n + p + q;
	for ( int i = 1; i <= n; ++i ) Add( i, i + n, 1 ), Add( i + n, i, 0 );
	for ( int i = 1; i <= p; ++i ) Add( S, i + n + n, 1 ), Add( i + n + n, S, 0 );
	for ( int i = 1; i <= q; ++i ) Add( i + n + n + p, T, 1 ), Add( T, i + n + n + p, 0 );

	for ( int i = 1; i <= n; ++i )
		for ( int j = 1; j <= p; ++j ){
			int t; scanf( "%d", &t );
			if ( t ) Add( j + n + n, i, 1 ), Add( i, j + n + n, 0 );
		}
	for ( int i = 1; i <= n; ++i )
		for ( int j = 1; j <= q; ++j ){
			int t; scanf( "%d", &t );
			if ( t ) Add( i + n, j + n + n + p, 1 ), Add( j + n + n + p, i + n, 0 );
		}
	int t;
	while( BFS() )
		while( ( t = DFS( S, 0x7f7f7f7f ) ) > 0 ) ans += t;
	printf( "%d\n", ans );
	return 0;
}

总结

这类题目如果要用网络最大流解决，一般来说，将“选择者”放中间，并且要拆点，“被选物”放两边，直接与源点、汇点相连。但是这种做法“被选物”不能多于两种。

如果多于两种，要怎么做呢？ 我也不知道 QAQ）求教大佬QAQ