【转载】Combination Sum

Combination Sum

Given a set of candidate numbers (C) and a target number (T), find all unique combinations in C where the candidate numbers sums to T.

The same repeated number may be chosen from C unlimited number of times.

Note:

• All numbers (including target) will be positive integers.
• Elements in a combination (a₁, a₂, … ,a_k) must be in non-descending order. (ie, a₁ ≤ a₂ ≤ … ≤ a_k).
• The solution set must not contain duplicate combinations.

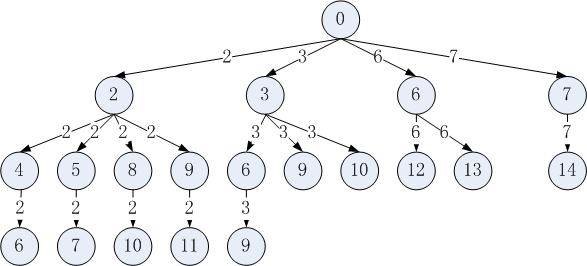
For example, given candidate set 2,3,6,7 and target 7, 
A solution set is: 
[7] 
[2, 2, 3]

 /** 整理的提交代码
  * 处理复杂度为
  * 主要思路：与Combination Sum不同之处在与每轮每个候选数字只能取一次，所以下次递归时考虑的当前元素的之后的元素
  *     所以这次在index中存放的下标是当前元素的下一个位置，以便递归时直接跳过上次考察过的元素，避免重复考察。
  *     但是在记录结果时需要回复记录在index中的下标。
  *       回溯法http://www.leetcode.com/2010/09/print-all-combinations-of-number-as-sum.html
  * 提交结果：
  * (Judge Small)
  * Run Status: Accepted!
  * Program Runtime: 4 milli secs （基本在几毫秒）
  * Progress: 22/22 test cases passed.
  * (Judge Large)
  * Run Status: Accepted!
  * Program Runtime: 144 milli secs    （基本稳定在一百四十几毫秒左右）
  * Progress: 172/172 test cases passed.
  */
 #include <vector>
 #include <algorithm>
 #include <functional>
 #include <iostream>
 using namespace std;

 class Solution {
 private:
     const int index_count;
     vector<vector<int> > results;
 public:
     Solution() : index_count() {};
     // index记录当前找到的候选数字，n表示当前正在找第几个，n是index的下标不是candidates的下标
     void backtrace(int target, int sum, vector<int> &candidates, int index[], int n)
     {
         if (sum > target)
         {
             return;    // 回溯
         }
         if (sum == target)
         {
             vector<int> result;
             for (int i = ; i <= n; ++i)
             {
                 result.push_back(candidates[index[i]-]);    // 这里需要减一，因为下面每次记录索引时加了1
             }
             results.push_back(result);
             return;    // 此处可以不加，如果不加return由于都是正整数，到下面的计算时会多进行一次无用的递归。
         }

         // 深度搜索，为了避免重复，每次从当前候选项索引到结尾，上面的i=index[n]可以看出
         for (int i = index[n]; i < candidates.size(); ++i)
         {
             index[n+] = i+;    // 记录当前考察的候选项索引并加一，下次考察是跳过上次考察过的元素，每轮每个元素值考察一次
             backtrace(target, sum+candidates[i], candidates, index, n+);
         }
     }
     vector<vector<int> > combinationSum2(vector<int> &candidates, int target) {
         // Start typing your C/C++ solution below
         // DO NOT write int main() function
         sort(candidates.begin(), candidates.end());

         int *index = new int[index_count];
         memset(index, , sizeof(int)*index_count);

         results.clear();    // 提交到leetcode的测试系统上必须添加，它应该是使用一个对象测试所有测试用例。
         backtrace(target, , candidates, index, );

         delete[] index;

         // 去重
         vector<vector<int> >::iterator end = results.end();
         sort(results.begin(), end, less<vector<int> >());
         vector<vector<int> >::iterator new_end = unique(results.begin(), results.end());
         results.erase(new_end, end);

         return results;
     }
 };

 int main()
 {
     vector<int> candidates;
     int number;
     cout << "input candidates: ";
     while (cin >> number)
     {
         candidates.push_back(number);
     }

     // 清除缓冲区
     cin.sync();
     cin.clear();

     int target;
     cout << "input target: ";
     cin >> target;

     vector<vector<int> > result;
     Solution s;
     result = s.combinationSum2(candidates, target);

     for (size_t i = ; i < result.size(); ++i)
     {
         for (size_t j = ; j < result[i].size(); ++j)
         {
             cout << result[i][j] << ' ';
         }
         cout << endl;
     }
     cout << endl;

     return ;
 }