机器学习作业（一）线性回归——Python(numpy)实现

题目太长啦！文档下载【传送门】

第1题

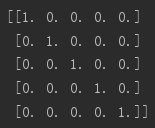
简述：设计一个5*5的单位矩阵。

 import numpy as np
 A = np.eye(5)
 print(A)

运行结果：

第2题

简述：实现单变量线性回归。

 import numpy as np
 import matplotlib.pyplot as plt
 from mpl_toolkits.mplot3d import Axes3D
 
 #-----------------计算代价值函数-----------------------
 def computeCost(X, y, theta):
     m = np.size(X[:,0])
     J = 1/(2*m)*np.sum((np.dot(X,theta)-y)**2)
     return J
 
 #----------------根据人口预测利润----------------------
 #读取数据集中数据，第一列是人口数据，第二列是利润数据
 data = np.loadtxt('ex1data1.txt',delimiter=",",dtype="float")
 m = np.size(data[:,0])
 # print(data)
 
 #------------------绘制样本点--------------------------
 X = data[:,0:1]
 y = data[:,1:2]
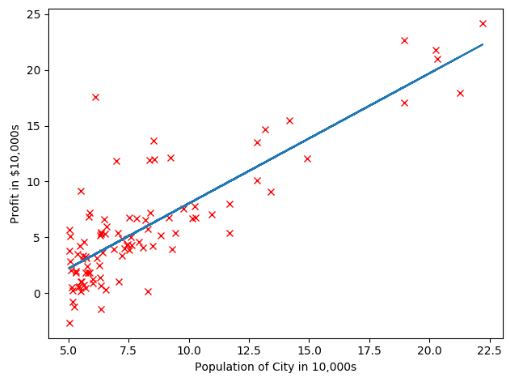
 plt.plot(X,y,"rx")
 plt.xlabel('Population of City in 10,000s')
 plt.ylabel('Profit in $10,000s')
 # plt.show()
 
 #-----------------梯度下降计算局部最优解----------------
 #添加第一列1
 one = np.ones(m)
 X = np.insert(X,0,values=one,axis=1)
 # print(X)
 
 #设置α、迭代次数、θ
 theta = np.zeros((2,1))
 iterations = 1500
 alpha = 0.01
 
 #梯度下降，并显示线性回归
 J_history = np.zeros((iterations,1))
 for iter in range(0,iterations):
     theta = theta - alpha/m*np.dot(X.T,(np.dot(X,theta)-y))
     J_history[iter] = computeCost(X,y,theta)
 plt.plot(data[:,0],np.dot(X,theta),'-')
 plt.show()
 # print(theta)
 # print(J_history)
 
 #--------------------显示三维图------------------------
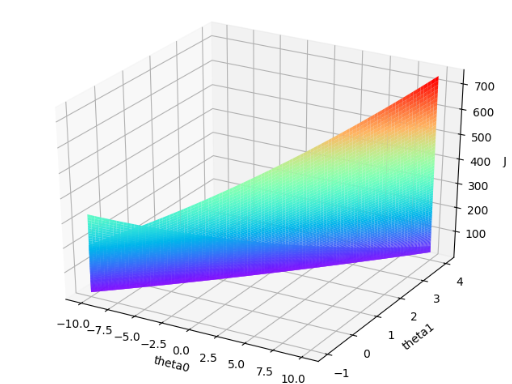
 theta0 = np.linspace(-10,10,100)
 theta1 = np.linspace(-1,4,100)
 J_vals = np.zeros((np.size(theta0),np.size(theta1)))
 for i in range(0,np.size(theta0)):
     for j in range(0,np.size(theta1)):
         t = np.asarray([theta0[i],theta1[j]]).reshape(2,1)
         J_vals[i,j] = computeCost(X,y,t)
 # print(J_vals)
 J_vals = J_vals.T    #需要转置一下，否则轴会反
 fig1 = plt.figure()
 ax = Axes3D(fig1)
 ax.plot_surface(theta0,theta1,J_vals,rstride=1,cstride=1,cmap=plt.get_cmap('rainbow'))
 ax.set_xlabel('theta0')
 ax.set_ylabel('theta1')
 ax.set_zlabel('J')
 plt.show()
 
 #--------------------显示轮廓图-----------------------
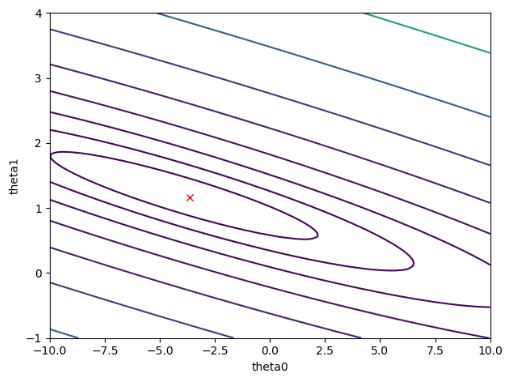
 lines = np.logspace(-2,3,20)
 plt.contour(theta0,theta1,J_vals,levels = lines)
 plt.xlabel('theta0')
 plt.ylabel('theta1')
 plt.plot(theta[0],theta[1],'rx')
 plt.show()

运行结果：

第3题

简述：实现多元线性回归。

 import numpy as np
 import matplotlib.pyplot as plt
 
 #-----------------计算代价值函数-----------------------
 def computeCost(X, y, theta):
     m = np.size(X[:,0])
     J = 1/(2*m)*np.sum((np.dot(X,theta)-y)**2)
     return J
 
 #-------------------根据面积和卧室数量预测房价----------
 #读取数据集中数据，第一列是面积数据，第二列是卧室数量，第三列是房价
 data = np.loadtxt('ex1data2.txt',delimiter=",",dtype="float")
 m = np.size(data[:,0])
 # print(data)
 X = data[:,0:2]
 y = data[:,2:3]
 
 #----------------------均值归一化---------------------
 mu = np.mean(X,0)
 sigma = np.std(X,0)
 X_norm = np.divide(np.subtract(X,mu),sigma)
 one = np.ones(m)   #添加第一列1
 X_norm = np.insert(X_norm,0,values=one,axis=1)
 # print(mu)
 # print(sigma)
 # print(X_norm)
 
 #----------------------梯度下降-----------------------
 alpha = 0.05
 num_iters = 100
 theta = np.zeros((3,1));
 J_history = np.zeros((num_iters,1))
 for iter in range(0,num_iters):
     theta = theta - alpha/m*np.dot(X_norm.T,(np.dot(X_norm,theta)-y))
     J_history[iter] = computeCost(X_norm,y,theta)
 # print(theta)
 x_col = np.arange(0,num_iters)
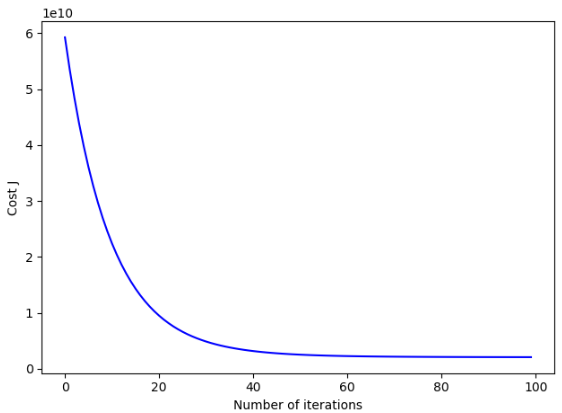
 plt.plot(x_col,J_history,'-b')
 plt.xlabel('Number of iterations')
 plt.ylabel('Cost J')
 plt.show()
 
 #----------使用上述结果对[1650,3]的数据进行预测--------
 test1 = [1,1650,3]
 test1[1:3] = np.divide(np.subtract(test1[1:3],mu),sigma)
 price = np.dot(test1,theta)
 print(price)        #输出预测结果[292455.63375132]
 
 #-------------使用正规方程法求解----------------------
 one = np.ones(m)
 X = np.insert(X,0,values=one,axis=1)
 theta = np.dot(np.dot(np.linalg.pinv(np.dot(X.T,X)),X.T),y)
 # print(theta)
 price = np.dot([1,1650,3],theta)
 print(price)       #输出预测结果[293081.46433497]

运行结果：【一个疑惑>>两种方法求解的估算价格很小，但θ相差较大？】