【杂题总汇】HDU-5215 Cycle

◆HDU-5215◆ Cycle

国庆节集训的第三天……讲图论，心情愉快……刷了一堆水题，不过也刷了一些有意思的题

+传送门+ HDU

---

▶ 题目

给出一个无向图（无自环，无重边），求该无向图中是否存在奇环、偶环。

多组数据，每组数据第一行为n,m表示点和边的数量，接下来m行每行描述一条边。

对于每组数据，输出两行，第一行输出是否存在奇环，第二行输出是否存在偶环。

---

▶ 解析

因为是一个简单图，这道题就简单了很多。

（1）判断奇环

有一类图是不包含奇数环的——二分图，反过来也是这样——二分图是不包含奇数环的图，所以不是二分图的图就一定包含奇数图。我们就只需要判断原图是否是二分图即可~ 黑白染色判断二分图就可以了。

（2）判断偶环

重点和难点基本上就在这儿了。

我们知道对于每一个连通块我们可以生成一棵DFS树，树上存在树边和返祖边（对这方面知识不熟的reader们建议先学了DFS树再看）。而一些树边和一条返祖边就会构成一个环——如果一条返祖边的两端点在DFS树上的路径距离为奇数，那么加上返祖边就形成了一个偶环。

当然形成偶环也不止这一个情况——看下面两种：

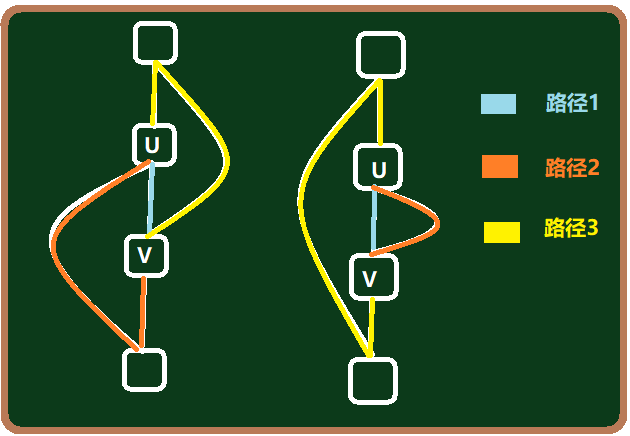
所以总结一下——另一种情况，存在两组点(a,b)(c,d)，a与b、c与d在树上的距离都为偶数（如果为奇数的话加上一条返祖边就可以直接形成偶数环了），且a->b和c->d的路径相交（点相交即可），那么就存在偶环，即路径2+路径3。

如上图所示，两个返祖边的端点之间的树边有交集 路径1 ，所以它们可以形成偶数环。

（3）具体实现

听起来像需要2次DFS，但是其实只需要一次——DFS可以同时实现判断二分图和树边、返祖边。

由于可能存在多个连通块，所以依次枚举起点u，如果u没有访问过，则从u开始遍历连通块，同时将u先染色。

若当前在节点u，则通过邻接表遍历u的儿子v，注意枚举v时要将v到达u的父亲的情况舍去。若发现v没有被遍历过，则将v染色后继续从v点遍历；否则经过了一条返祖边，判断v的颜色：

① col[v] ≠ col[u] ： 则u->v的路径为奇数，二分图染色成功，存在偶环；

② col[v] = col[u] ： 则u->v的理解为偶数，存在奇环；遍历u->v的路径，如果路径上有点已经被打上标记，则说明有另外一条返祖边的两端点之间的路径与当前u->v的路径相交，存在偶环，否则将 u->v 的路径上的点全部打上标记；

输出即可。

---

▶ 源代码

 /*Lucky_Glass*/
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<vector>
 using namespace std;
 const int N=int(1e5);
 int n,m;
 vector<int> lnk[N+];
 int col[N+],fa[N+],dep[N+];
 bool cov[N+];
 bool odd,eve;
 void DFS(int u,int pre){
     for(int i=;i<(int)lnk[u].size();i++){
         int v=lnk[u][i];
         if(v==pre) continue;
         if(col[v]==-){
             col[v]=!col[u];
             fa[v]=u;
             dep[v]=dep[u]+;
             DFS(v,u);
         }
         else{
             if(col[v]==col[u]){
                 odd=true;
                 if(dep[v]>dep[u]) continue; //upd. 每条返祖边只能走一次！
                 if(cov[v]) eve=true;
                 else cov[v]=true;
                 int pnt=u;
                 while(!eve){
                     if(cov[pnt]) eve=true;
                     cov[pnt]=true;
                     pnt=fa[pnt];
                     if(pnt==v || pnt==-) break;
                 }
             }
             else eve=true;
         }
     }
 }
 void Clear(){
     memset(cov,false,sizeof cov);
     memset(fa,-,sizeof fa);
     memset(lnk,,sizeof lnk);
     memset(col,-,sizeof col);
     memset(dep,,sizeof dep);
     odd=eve=false;
 }
 int main(){
     int T;scanf("%d",&T);
     while(T--){
         Clear();
         scanf("%d%d",&n,&m);
         for(int i=;i<m;i++){
             int u,v;
             scanf("%d%d",&u,&v);
             lnk[u].push_back(v);
             lnk[v].push_back(u);
         }
         for(int i=;i<=n;i++)
             if(col[i]==-){
                 col[i]=;
                 dep[i]=;
                 DFS(i,-);
             }
         printf("%s\n%s\n",odd?"YES":"NO",eve?"YES":"NO");
     }
     return ;
 }

　　

---

The End

Thanks for reading!

- Lucky_Glass

（Tab：如果我有没讲清楚的地方可以直接在邮箱lucky_glass@foxmail.com email我，在周末我会尽量解答并完善博客~