Fraction

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others)

Total Submission(s): 1010    Accepted Submission(s): 532

Problem Description

Mr. Frog recently studied how to add two fractions up, and he came up with an evil idea to trouble you by asking you to calculate the result of the formula below: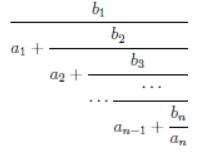

As a talent, can you figure out the answer correctly?

Input

The first line contains only one integer T, which indicates the number of test cases.

For each test case, the first line contains only one integer n (n≤8).

The second line contains n integers: a1,a2,⋯an(1≤ai≤10).
The third line contains n integers: b1,b2,⋯,bn(1≤bi≤10).

Output

For each case, print a line “Case #x: p q”, where x is the case number (starting from 1) and p/q indicates the answer.

You should promise that p/q is irreducible.

Sample Input

1

2

1 1

2 3

Sample Output

Case #1: 1 2

Hint

Here are the details for the first sample: 2/(1+3/1) = 1/2

//题意很容易理解，就是求出这样的式子的分子，分母最简形式

模拟一下即可

 #include <iostream>
 #include <math.h>
 #include <stdio.h>
 using namespace std;
 #define MX 105
 int n;
 int A[MX];
 int B[MX];

 int gcd(int a,int b)
 {
     return b==?a:gcd(b,a%b);
 }

 int main()
 {
     int T;
     scanf("%d",&T);
     for (int cnt=;cnt<=T;cnt++)
     {
         scanf("%d",&n);
         for (int i=;i<=n;i++)
             scanf("%d",&A[i]);
         for (int i=;i<=n;i++)
             scanf("%d",&B[i]);
         int p=B[n],q=A[n];
         int a,b;
         for (int i=n-;i>=;i--)
         {
             a = A[i],b = B[i];
             a = a*q + p;
             b = b*q;

             p = b ;
             q = a;
         }
         int yue = gcd(p,q);
         printf("Case #%d: %d %d\n",cnt,p/yue,q/yue);
     }
     return ;
 }