动态规划（二）——背包dp

01背包问题（每个物品最多选一次）

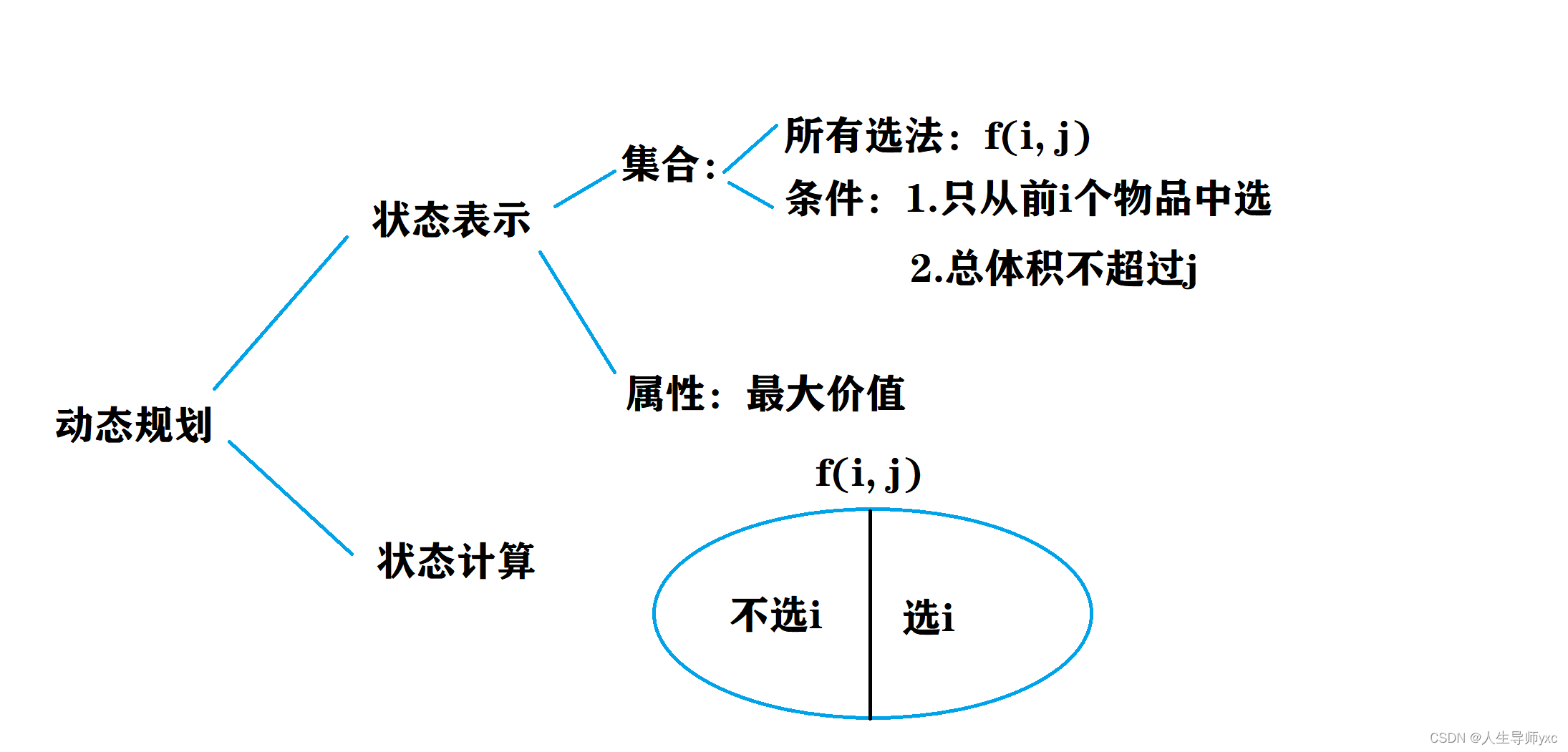
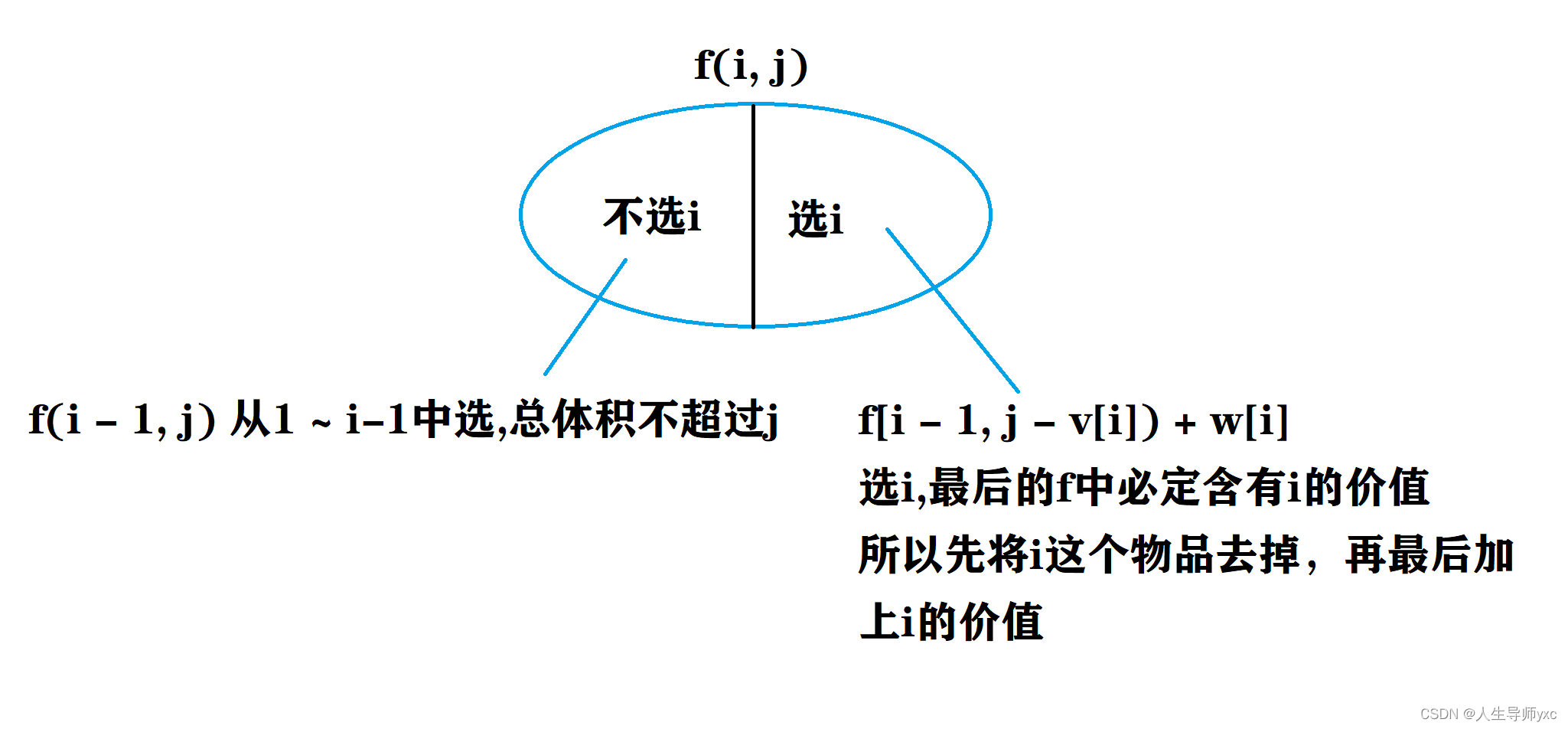
AcWing 2. 0/1背包问题

朴素の版本：

#include <bits/stdc++.h>
using namespace std;
const int N=1010;
int vi[N],wi[N],f[N][N];
int n,v;
int main(){
	scanf("%d%d",&n,&v);
	for(int i=1;i<=n;i++) scanf("%d%d",&vi[i],&wi[i]);
	for(int i=1;i<=n;i++){
		for(int j=0;j<=v;j++){
			f[i][j]=f[i-1][j];
			if(j>=v[i]) f[i][j]=max(f[i][j],f[i-1][j-vi[i]]+wi[i]);
		}
	}
	printf("%d",f[n][v]);
	return 0;
}

滚动数组优化の版本：

#include <bits/stdc++.h>
using namespace std;
const int N=1010;
int vi[N],wi[N],f[N][N];
int n,v;
int main(){
	scanf("%d%d",&n,&v);
	for(int i=1;i<=n;i++) scanf("%d%d",&vi[i],&wi[i]);
	for(int i=1;i<=n;i++){
		for(int j=0;j<=v;j++){
			f[i&1][j]=f[(i-1)&1][j];
			if(j>=v[i]) f[i&1][j]=max(f[i&1][j],f[(i-1)&1][j-vi[i]]+wi[i]);
		}
	}
	printf("%d",f[n&1][v]);
	return 0;
}

有不了解滚动数组的读者，可以参考以下大佬博客:

https://www.cnblogs.com/kimsimple/p/6883871.html

终极优化の版本：（二维变一维）

#include <bits/stdc++.h>
using namespace std;
const int N=1010;
int vi[N],wi[N],f[N];
int n,v;
int main(){
	scanf("%d%d",&n,&v);
	for(int i=1;i<=n;i++) scanf("%d%d",&vi[i],&wi[i]);
	for(int i=1; i<=n; i++){
		for(int j=v; j>=vi[i]; j--){
			f[j]=max(f[j],f[j-vi[i]]+wi[i]);
		}
	}
	printf("%d", f[v]);
	return 0;
}

完全背包问题（每个物品可以选无限多次）

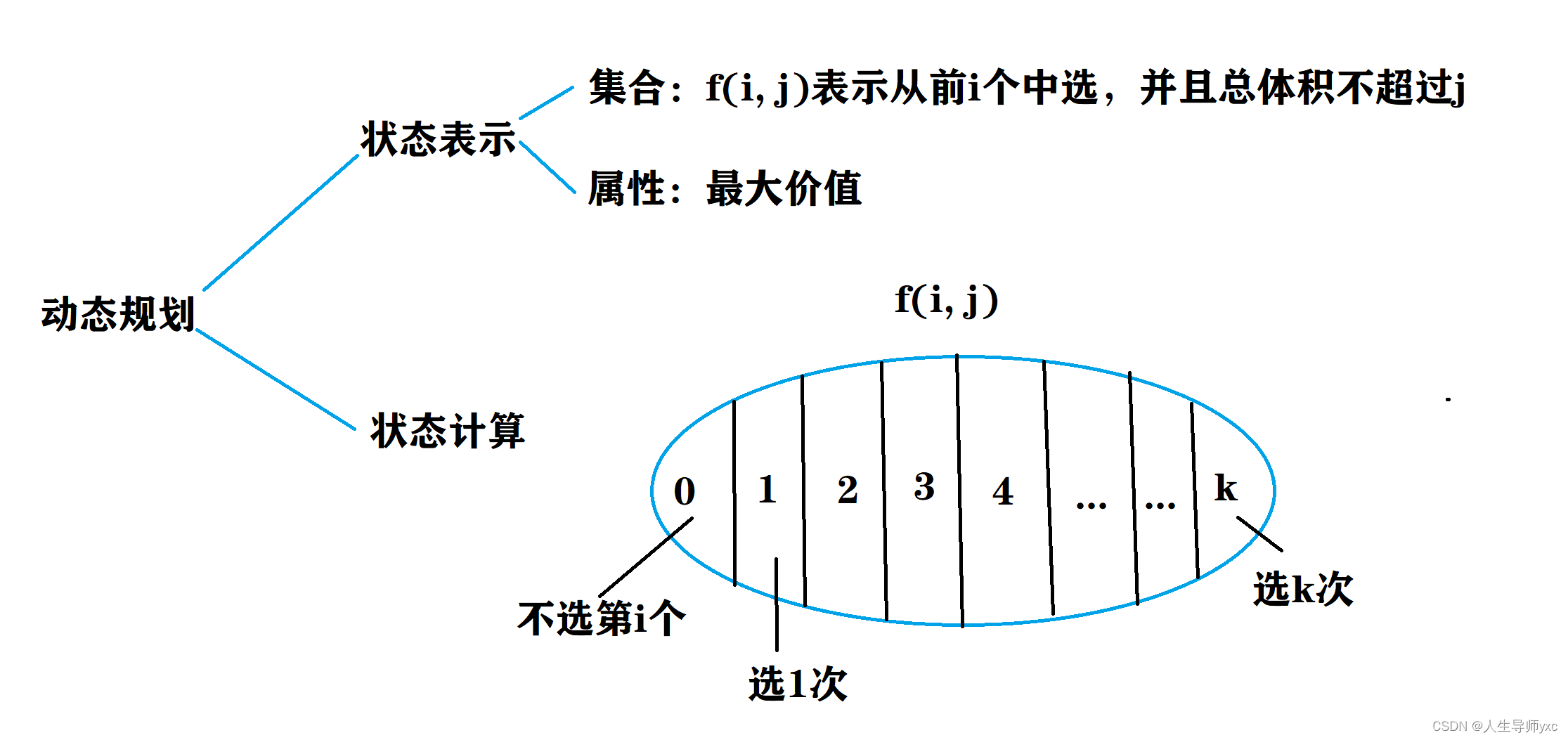
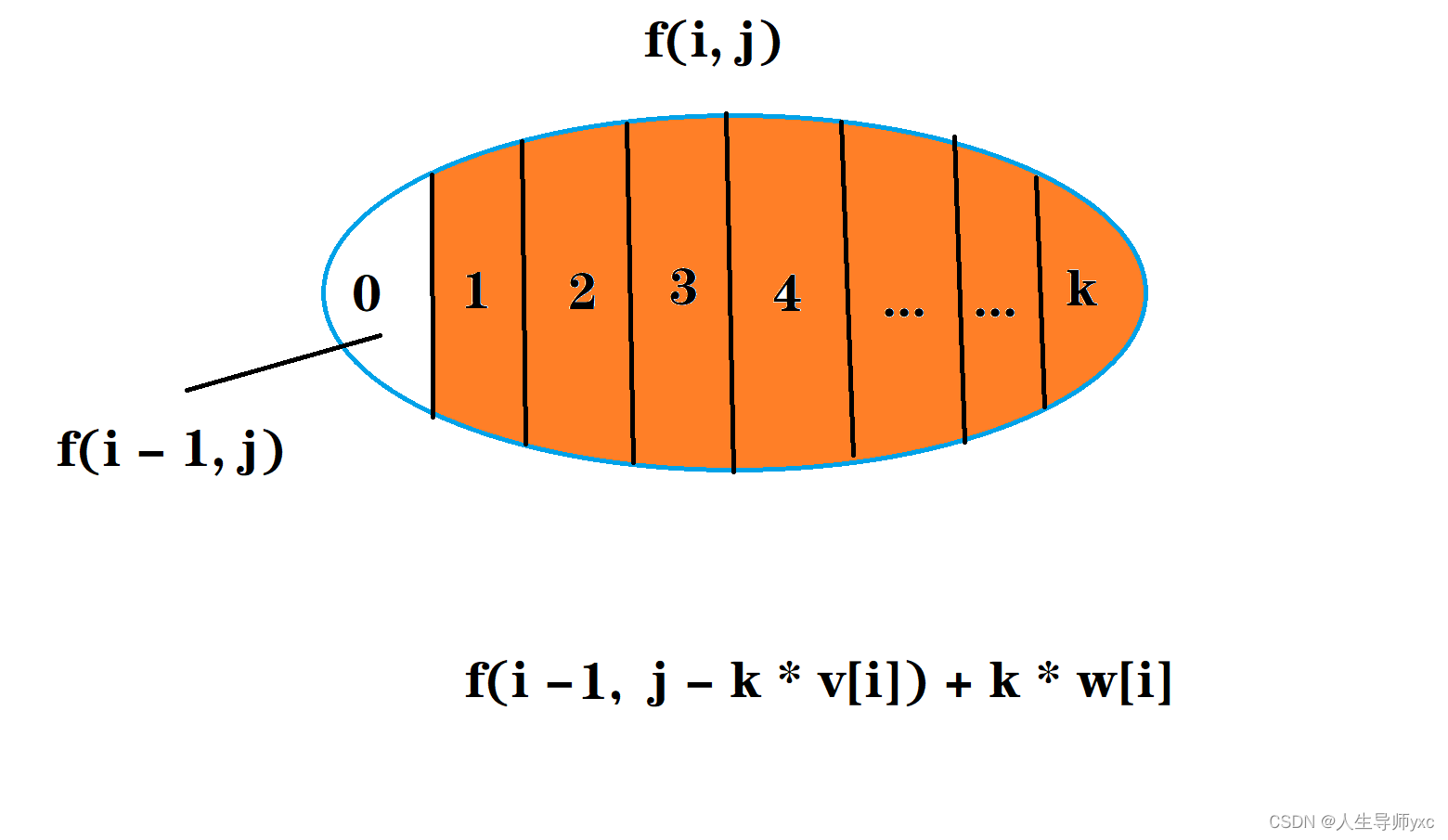
AcWing 3. 完全背包问题

朴素の版本：

#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
int vi[N],wi[N],f[N][N];
int n,v;
int main(){
	scanf("%d%d",&n,&v);
	for(int i=1;i<=n;i++) scanf("%d%d",&vi[i],&wi[i]);
	for(int i=1;i<=n;i++){
		for(int j=0;j<=v;j++){
			for(int k=0;k*vi[i]<=j;k++){
				f[i][j]=max(f[i][j],f[i-1][j-k*vi[i]]+k*wi[i]);
			}
		}
	}
	printf("%d", f[n][v]);
	return 0;
}

二维数组の版本：

二维数组优化の版本：

#include <bits/stdc++.h>
using namespace std;
const int N=1010;
int vi[N],wi[N],f[N][N];
int n,v;
int main(){
	scanf("%d%d",&n,&v);
	for(int i=1;i<=n;i++) scanf("%d%d",&vi[i],&wi[i]);
	for(int i=1;i<=n;i++){
		for(int j=0;j<=v;j++){
			f[i][j]=f[i-1][j];
			if(j>=vi[i]) f[i][j]=max(f[i][j],f[i][j-vi[i]]+wi[i]);
		}
	}
	printf("%d",f[n][v]);
	return 0;
}

终极优化の版本：

#include <bits/stdc++.h>
using namespace std;
const int N=1010;
int vi[N],wi[N],f[N];
int n,v;
int main(){
	scanf("%d%d",&n,&v);
	for(int i=1;i<=n;i++) scanf("%d%d",&vi[i],&wi[i]);
	for(int i=1;i<=n;i++){
		for(int j=vi[i];j<=v;j++){
			f[j]=max(f[j],f[j-vi[i]]+wi[i]);
		}
	}
	printf("%d",f[v]);
	return 0;
}

多重背包问题（有限次地选每件物品）---二进制优化版本

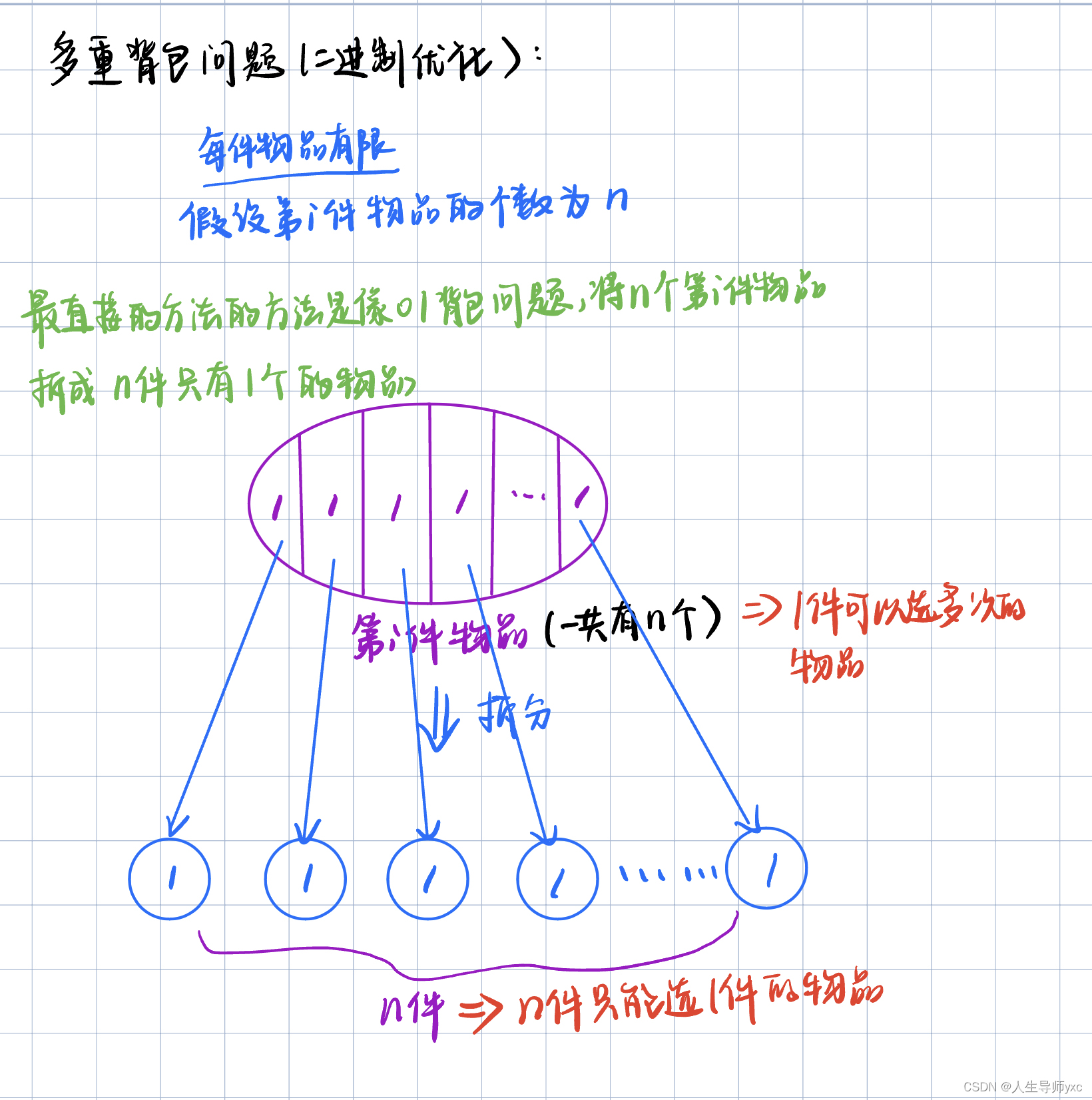
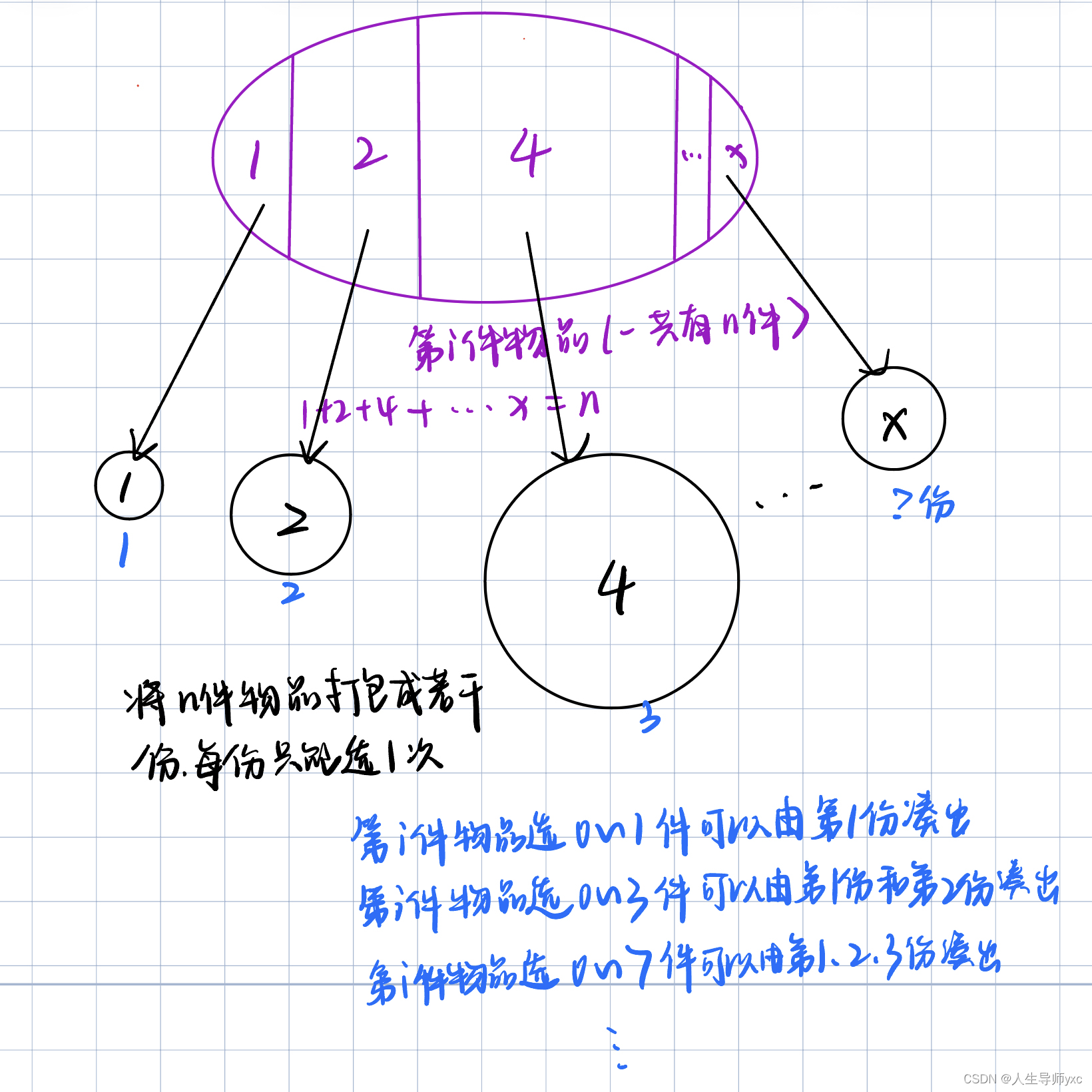
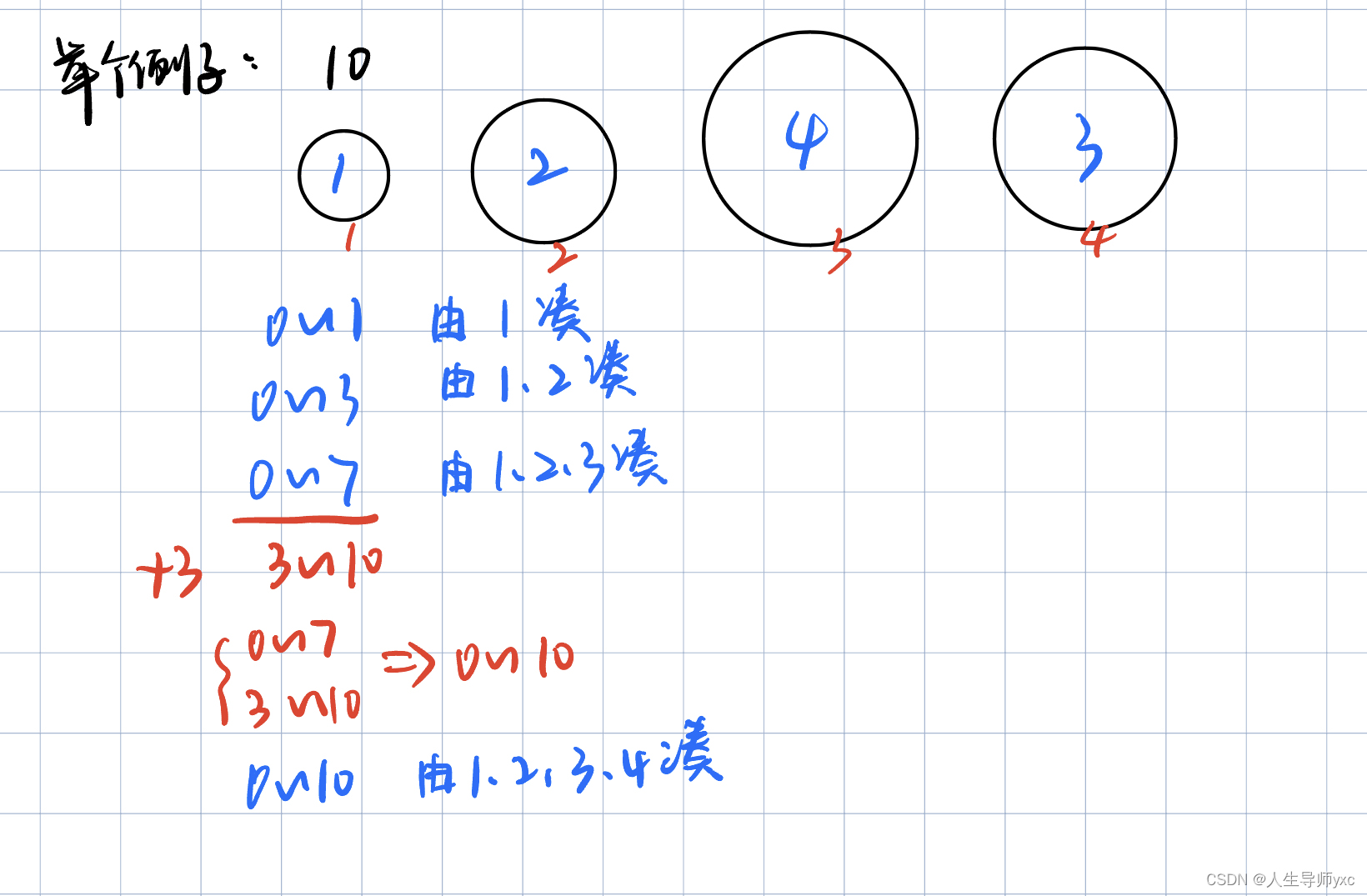
多重背包问题

二进制拆分の版本：

#include <bits/stdc++.h>
using namespace std;
const int N=15000;
const int M=2010;
int n,m,cnt;
int f[M];
int v[N],w[N],s[N];
int main(){
	int vi=0,wi=0,si=0;
	scanf("%d%d", &n, &m);
	//二进制拆分
	for(int i=1;i<=n;i++){
		scanf("%d%d%d",&vi,&wi,&si);
		if(si>m/vi) si=m/vi;
		for(int j=1;j<=si;j<<=1){
			v[++cnt]=j*vi;
			w[cnt]=j*wi;
			si-=j;
		}
		if(si>0){
			v[++cnt]= si*vi;
			w[cnt]=si*wi;
		}
	}
	//0/1背包
	for(int i=1;i<=cnt;i++){
		for(int j=m;j>=v[i];j--){
			f[j] = max(f[j],f[j-v[i]]+w[i]);
		}
	}
	printf("%d",f[m]);
	return 0;
}

分组背包问题（n组,每组只能选一种并且最多选一次）

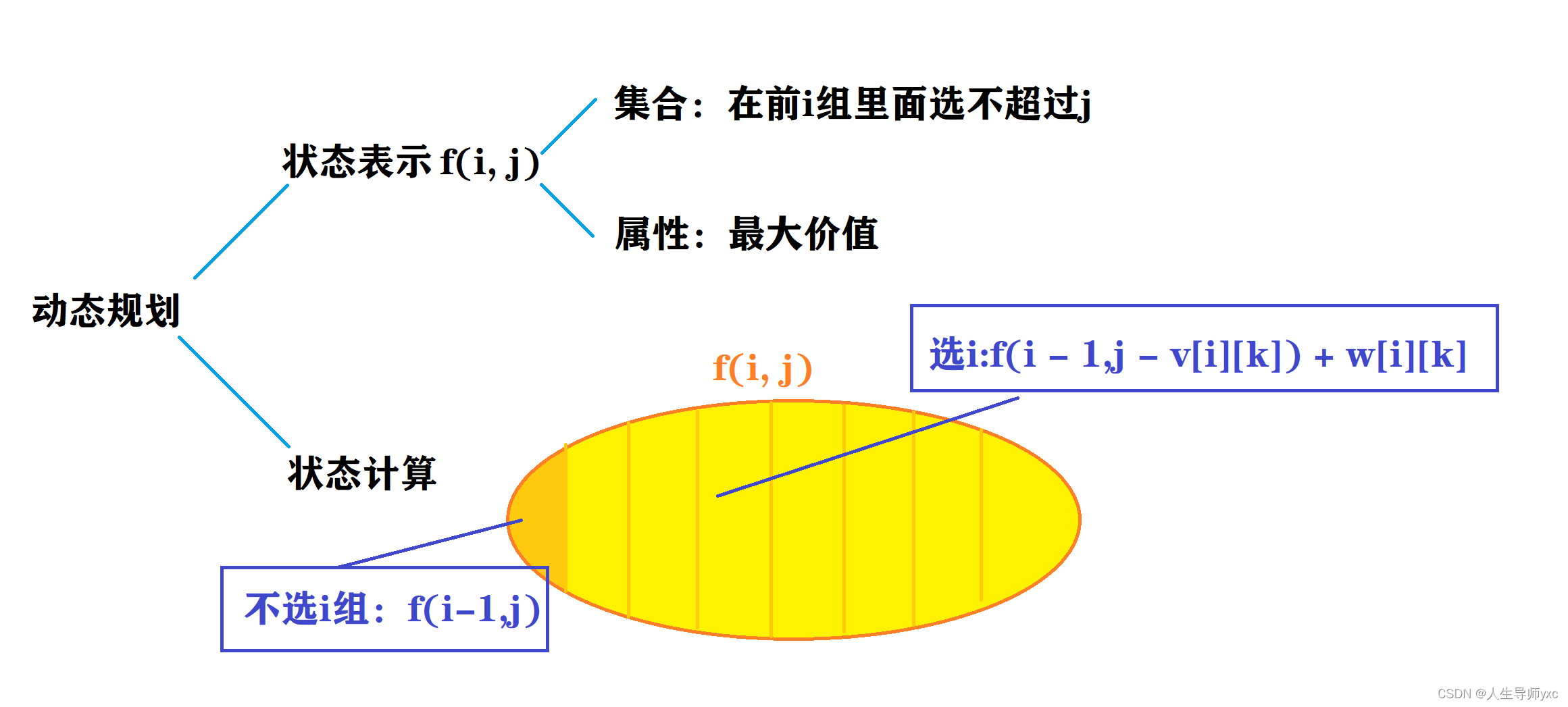
分组背包问题

朴素の版本：

#include <bits/stdc++.h>
using namespace std;
const int N=40;
const int M=210;
int n,m,t;
int v[N],c[N];
int g[15][N],f[15][M];
int main(){
	int x=0;
	scanf("%d%d%d",&m,&n,&t);
	for(int i=1;i<=n;i++){
		scanf("%d%d%d",&v[i],&c[i],&x);
		g[x][++g[x][0]]=i;
	}

	for(int i=1;i<=t;i++){
		for(int j=0;j<=m;j++){
			f[i][j]=f[i-1][j];
			for(int k=1;k<=g[i][0];k++){
				if(j>=v[g[i][k]]) {
					x=g[i][k];
					f[i][j]=max(f[i][j],f[i-1][j-v[x]]+c[x]);
				}
			}
		}
	}
	printf("%d",f[t][m]);
	return 0;
}

终极优化の版本：

#include <bits/stdc++.h>
using namespace std;
const int N=40;
const int M=210;
int n,m,t;
int v[N],c[N],g[15][N];
int f[M];
int main(){
	int x=0;
	scanf("%d%d%d",&m,&n,&t);
	for(int i=1;i<=n;i++){
		scanf("%d%d%d",&v[i],&c[i],&x);
		g[x][++g[x][0]]=i;
	}

	for(int i=1;i<=t;i++){
		for(int j=m;j>=0;j--){
			for(int k=1; k<=g[i][0]; k++){
				if(j>=v[g[i][k]]) {
					x=g[i][k];
					f[j]=max(f[j],f[j-v[x]]+c[x]);
				}
			}
		}
	}
	printf("%d",f[m]);
	return 0;
}

以上就是背包dp中几个类型的问题了，如有错误欢迎大家在评论区指正小蒟蒻博主的错误~

本文图片来自https://blog.csdn.net/m0_73569492/article/details/129864277鸣谢大佬

#一名爱打篮球的oier#