SPOJ 839 Optimal Marks（最小割的应用）

https://vjudge.net/problem/SPOJ-OPTM

题意：

给出一个无向图G，每个点 v 以一个有界非负整数 lv 作为标号，每条边e=（u，v）的权w定义为该边的两个端点的标号的异或值，即W=lu XOR lv。现已知其中部分点的标号，求使得该图的总边权和最小的标号赋值。即最小化：

思路：

这道题目在刘伯涛的论文里讲得十分的详细，看看论文就可以啦。

XOR运算是根据二进制的每一位来计算的，，并且因为每一位都是相互独立的，互不影响，所以可以转化为下式：

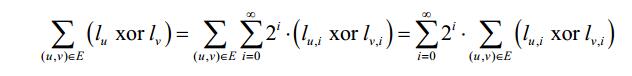
接下来对于每一位都新建图，对于已经标号的顶点来说，如果该位是1，则与源点相连，否则与汇点相连，容量均为INF。如果本来就相连的点还是需要相连的，容量为1。对于每个还没有标号的点来说，在这一位的取值要么是1，要么是0，这就很符合最小割。在跑完最大流之后，只需要从源点出发，凡是能到达的点都是取值为1的。

 #include<iostream>
 #include<algorithm>
 #include<cstring>
 #include<cstdio>
 #include<vector>
 #include<stack>
 #include<queue>
 #include<cmath>
 #include<map>
 #include<set>
 using namespace std;
 typedef long long ll;
 typedef pair<int,int> pll;
 const int INF = 0x3f3f3f3f;
 const int maxn =  + ;

 int n, m, k;
 int val[maxn];
 int ans[maxn];
 int vis[maxn];
 int mp[maxn][maxn];

 struct Edge
 {
     int from,to,cap,flow;
     Edge(int u,int v,int w,int f):from(u),to(v),cap(w),flow(f){}
 };

 struct Dinic
 {
     int n,m,s,t;
     vector<Edge> edges;
     vector<int> G[maxn];
     bool vis[maxn];
     int cur[maxn];
     int d[maxn];

     void init(int n)
     {
         this->n=n;
         for(int i=;i<n;++i) G[i].clear();
         edges.clear();
     }

     void AddEdge(int from,int to,int cap)
     {
         edges.push_back( Edge(from,to,cap,) );
         edges.push_back( Edge(to,from,,) );
         m=edges.size();
         G[from].push_back(m-);
         G[to].push_back(m-);
     }

     bool BFS()
     {
         queue<int> Q;
         memset(vis,,sizeof(vis));
         vis[s]=true;
         d[s]=;
         Q.push(s);
         while(!Q.empty())
         {
             int x=Q.front(); Q.pop();
             for(int i=;i<G[x].size();++i)
             {
                 Edge& e=edges[G[x][i]];
                 if(!vis[e.to] && e.cap>e.flow)
                 {
                     vis[e.to]=true;
                     d[e.to]=d[x]+;
                     Q.push(e.to);
                 }
             }
         }
         return vis[t];
     }

     int DFS(int x,int a)
     {
         if(x==t || a==) return a;
         int flow=, f;
         for(int &i=cur[x];i<G[x].size();++i)
         {
             Edge &e=edges[G[x][i]];
             if(d[e.to]==d[x]+ && (f=DFS(e.to,min(a,e.cap-e.flow) ) )>)
             {
                 e.flow +=f;
                 edges[G[x][i]^].flow -=f;
                 flow +=f;
                 a -=f;
                 if(a==) break;
             }
         }
         return flow;
     }

     int Maxflow(int s,int t)
     {
         this->s=s; this->t=t;
         int flow=;
         while(BFS())
         {
             memset(cur,,sizeof(cur));
             flow +=DFS(s,INF);
         }
         return flow;
     }
 }DC;

 void dfs(int u, int x)
 {
     vis[u]=;
     ans[u]+=x;
     for(int i=;i<DC.G[u].size();i++)
     {
         Edge& e=DC.edges[DC.G[u][i]];
         if(!vis[e.to] && e.cap>e.flow)
             dfs(e.to,x);
     }
 }

 void solve()
 {
     int src=,dst=n+;
     int bite=;
     while(true)
     {
         DC.init(dst+);
         for(int i=;i<=n;i++)
             for(int j=;j<=n;j++)
             if(mp[i][j]) DC.AddEdge(i,j,);

         bool flag=false;
         for(int i=;i<=n;i++)
         {
             if(val[i]!=-)
             {
                 if(val[i]>=)
                 {
                     flag=true;
                 }
                 if(val[i]&)
                 {
                     DC.AddEdge(src,i,INF);
                 }
                 else
                 {
                     DC.AddEdge(i,dst,INF);
                 }
                 val[i]>>=;
             }
         }

         if(!flag)  break;
         DC.Maxflow(src,dst);
         memset(vis,,sizeof(vis));
         dfs(src,bite);
         bite<<=;
     }
 }

 int main()
 {
     //freopen("in.txt","r",stdin);
     int T;
     scanf("%d",&T);
     while(T--)
     {
         memset(mp,,sizeof(mp));
         scanf("%d%d",&n,&m);
         for(int i=;i<m;i++)
         {
             int u,v;
             scanf("%d%d",&u,&v);
             mp[u][v]=mp[v][u]=;
         }
         memset(val,-,sizeof(val));
         scanf("%d",&k);
         for(int i=;i<k;i++)
         {
             int u,v;
             scanf("%d%d",&u,&v);
             val[u]=v;
         }
         memset(ans,,sizeof(ans));
         solve();
         for(int i=;i<=n;i++)
         {
             printf("%d\n",ans[i]);
         }
     }
     return ;
 }