第一步 生成对应的ssh key

　　　　1 后面输入你的用户名 或者 邮箱

2 输入一个独立的ssh key名字 区别之前的名字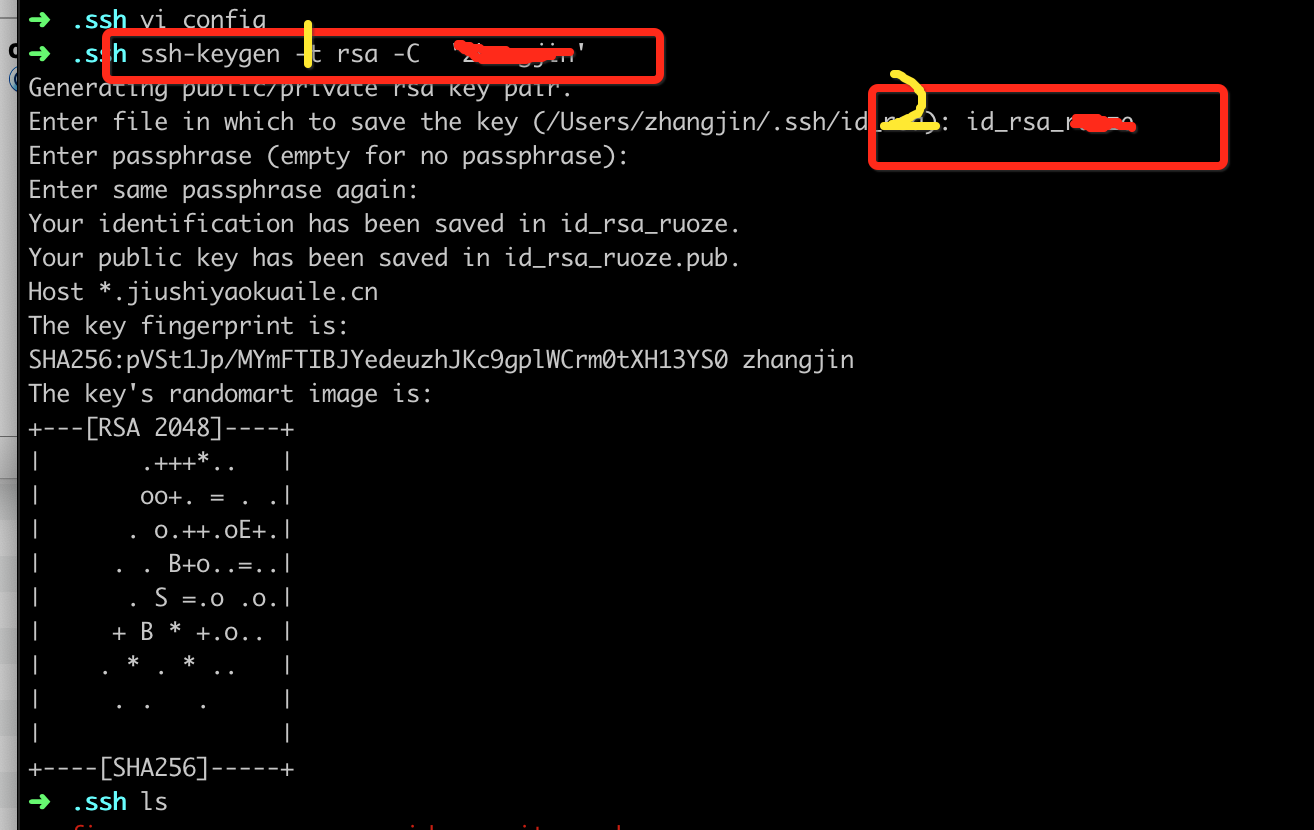

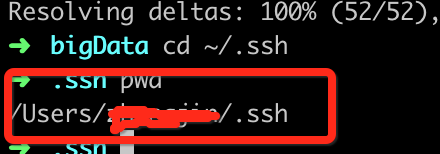
第二步  编辑 config文件

在.ssh/目录下面

　　　　　　

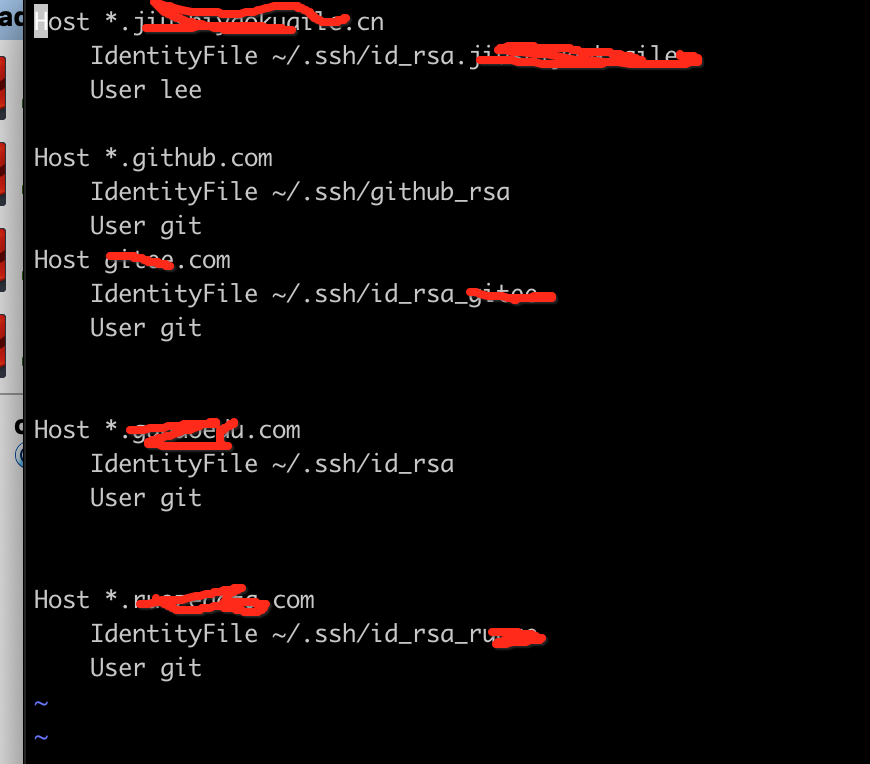
　　在config文件配置如下信息  对照你自己的远程git服务器域名 以及 本地生成sshke私钥名 以及 git用户添加

Host *.xxxxx.com

　　　　IdentityFile   ~/.ssh/id_rsa_xxx
　　　　User git

第三步 添加ssh key 到你的git服务

　　　　


~

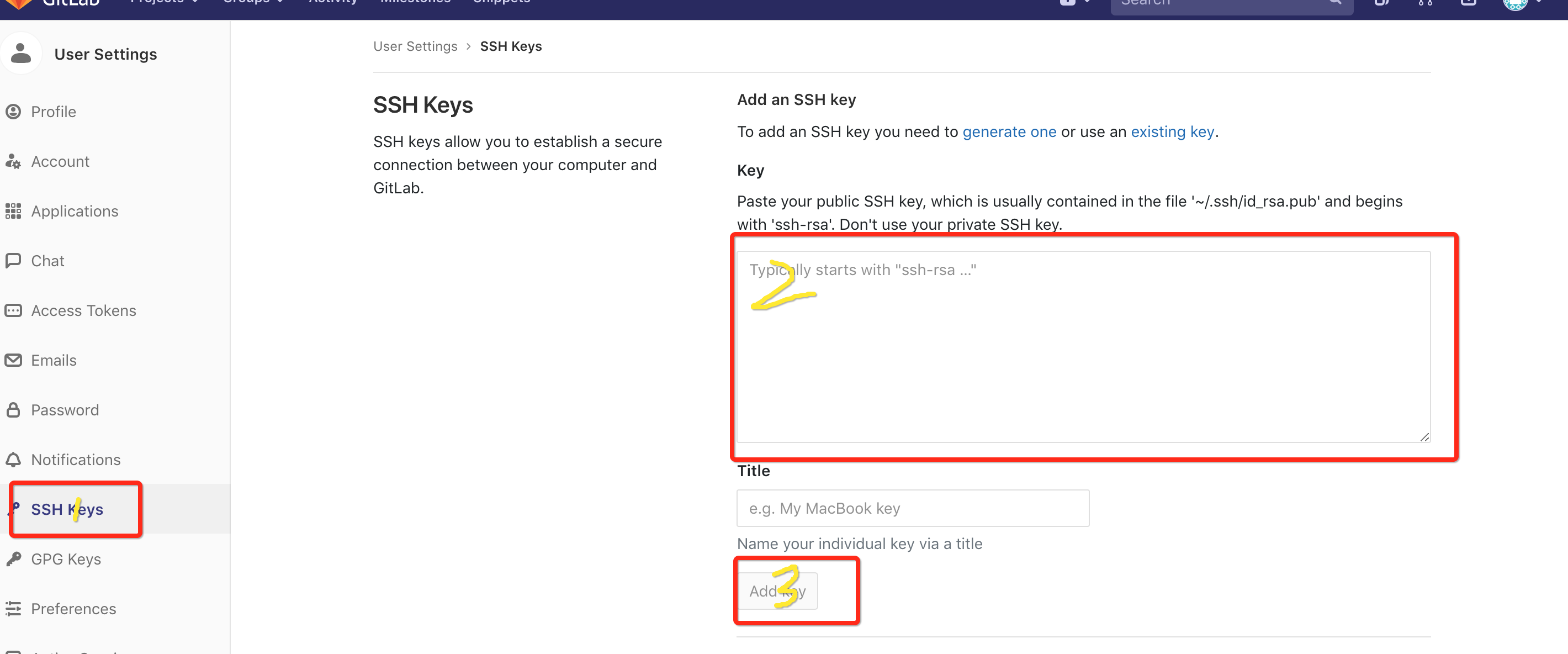
第四步 添加成功后 正常用ssh key的方式 git clone项目即可

Mac下配置多个SSH KEY访问远程Git服务的更多相关文章

  1. Mac下配置多个SSH Keys

    Mac下配置多个SSH Keys 生成SSH key # Creates a new ssh key using the provided email # 默认生成的文件名为id_rsa,可以根据命令 ...

  2. CAS (3) —— Mac下配置CAS客户端经代理访问Tomcat CAS

    CAS (3) -- Mac下配置CAS客户端经代理访问Tomcat CAS tomcat版本: tomcat-8.0.29 jdk版本: jdk1.8.0_65 nginx版本: nginx-1.9 ...

  3. Mac电脑用终端生成SSH key 访问自己的Github

    链接:https://www.jianshu.com/p/5b34b7b34cae

  4. CAS (7) —— Mac下配置CAS 4.x的JPATicketRegistry（服务端）

    CAS (7) -- Mac下配置CAS 4.x集群及JPATicketRegistry(服务端) tomcat版本: tomcat-8.0.29 jdk版本: jdk1.8.0_65 cas版本: ...

  5. 如何在Mac下配置Github和Bitbucket的SSH

    --- title: 如何在Mac下配置Github和Bitbucket的SSH date: 2017-12-23 21:10:30 tags: - Mac - Git - Github catego ...

  6. CAS (1) —— Mac下配置CAS到Tomcat（服务端）（转）

    tomcat版本: tomcat-8.0.29 jdk版本: jdk1.8.0_65 cas版本: cas4.1.2cas-client-3.4.1 参考来源: CAS实现单点登录(SSO)经典完整教 ...

  7. Mac下配置Apache Httpd的Https/SSL

    Mac下配置Apache Httpd的Https/SSL httpd版本: httpd-2.4.17 jdk版本: jdk1.8.0_65 参考来源: Mac下安装Apache Httpd Mac O ...

  8. CAS (1) —— Mac下配置CAS到Tomcat（服务端）

    CAS (1) -- Mac下配置CAS到Tomcat(服务端) tomcat版本: tomcat-8.0.29 jdk版本: jdk1.8.0_65 cas版本: cas4.1.2 cas-clie ...

  9. CAS (2) —— Mac下配置CAS到Tomcat（客户端）

    CAS (2) -- Mac下配置CAS到Tomcat(客户端) tomcat版本: tomcat-8.0.29 jdk版本: jdk1.8.0_65 cas版本: cas4.1.2 cas-clie ...

随机推荐

  1. 关于C# 怎么调用webapi来获取到json数据

      /// <summary>        /// 调用api返回json        /// </summary>        /// <param name=& ...

  2. day6 字符串

    重复输出字符串 # * 重复输出字符串 print("hello"*2) 字符串切片 # 字符串也拥有索引,和列表切片操作类似 print("helloworld&quo ...

  3. 【LightOJ 1136】Division by 3（简单数学）

    BUPT2017 wintertraining(16) #5 C HDU - 1021 题意 1, 12, 123, 1234, ..., 12345678910, ... 问第a到第b个数(incl ...

  4. [转]GDB

    gdb调试coredump文件 gcc -g main.c //在目标文件加入源代码的信息 gdb a.out (gdb) start //开始调试 (gdb) n //一条一条执行 (gdb) st ...

  5. BZOJ 1778: [Usaco2010 Hol]Dotp 驱逐猪猡

    1778: [Usaco2010 Hol]Dotp 驱逐猪猡 Time Limit: 10 Sec  Memory Limit: 64 MBSubmit: 563  Solved: 216[Submi ...

  6. csp20170304地铁修建_Solution

    ccf20170304地铁修建_Solution 这里最短路为所以从点1到点n的路径中最长的道路的长度. 因为1 ≤ n ≤ 100000,1 ≤ m ≤ 200000,属于稀疏图,所以使用Spfa( ...

  7. Linux：批量修改分隔符（awk、BEGIN、FS、OFS、print、tr命令）

    批量修改文件的分隔符,可以用FS和OFS命令 FS:Field Separator,字段分隔符 OFS:Out of Field Separator,输出字段分隔符 修改空格为分隔符 假设有这么一个文 ...

  8. FTP文件乱码和传输模式解释

    转: FTP文件乱码和传输模式解释 2017年02月18日 10:50:03 -Hermes- 阅读数:12112更多 所属专栏: 异常解决方案急诊室   版权声明:大侠,在转载时请注明出处,小弟不胜 ...

  9. 在windows上部署使用redis出现的问题及解决方法

    在windows上部署使用Redis出现问题的解决方法  原文链接:https://www.cnblogs.com/herry52/p/5938902.html 下载Redis 在Redis的官网下载 ...

  10. 惊喜的gift

    情侣的饰品吧!我之前在淘宝上买了一套,挺好的,很好看呢!男的手链,女的项链,手链需要项链的钥匙才能打得开,女孩子应该都会很喜欢的吧!至少我很喜欢!而且价格也不贵,150块人民币都不到,很适合当生日礼物 ...