Spring Boot下的lombok安装以及使用简介

引言：lombok是一套代码模板解决方案，将极大提升开发的效率，这里介绍给大家使用。

1. Lombok

lombok是一个可以通过简单的注解的形式来帮助我们简化消除一些必须有但显得很臃肿的 Java 代码的工具.例如,我们在项目中可能不可避免的使用到一些POJO类,这时候我们需要填充应有的字段,并手动建立构造函数,Getter,Setter等方法.而lombok就可以通过@Data注解的方式生成其属性的构造器,Getter,Setter,equals,toString等方法.在编译时这些方法会自动生成,在.class文件中,这些方法和我们手写Getter,Setter等方法是一样的.使用lombok减少了重复的创建那些方法的时间,并且可以使得代码更加简洁.

2. LomBok的安装

1.下载 lombok.jar  https://projectlombok.org/download.html
2.手动安装 
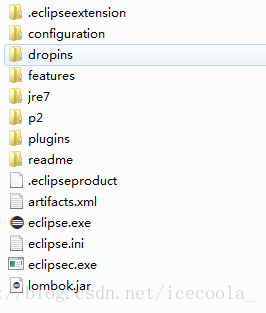
（1）将lombok.jar移到eclipse的安装目录 

（2）在eclipse.in文件最后加入下面两行

-Xbootclasspath/a:lombok.jar
-javaagent:lombok.jar

-javaagent:xxx.jar 的jar名称 需要与根目录下的jar名一致， 
不一致，可能会出现eclipse无法启动的情况。

3.重启eclipse

4.springboot使用lombok

在SpringBoot项目的pom.xml中新增如下信息：

 <dependency>
    <groupId>org.projectlombok</groupId>
    <artifactId>lombok</artifactId>
</dependency>

注意这里无需指定版本，因为Spring Boot中已经默认引入了这个类库，且指定了其scope。 这个即将lombok引入了项目，可以引用其类库标注。

3.   Lombok的使用

主要是基于标注来进行信息的封装和使用：

以下是一些常用的注解：

@NonNull：  标识对象是否为空，为空则抛出异常

@Getter:   自动生成Getter方法

@Setter:  自动生成Setter

@ToString：  覆盖tostring方法

　　@EqualsAndHashCode: 覆盖equal和hashCode方法

　　@Data:  @Getter/@Setter, @ToString, @EqualAndHashCode等组合，不包括构造函数

　　@NoArgsConstructor无参构造函数

　　@AllArgsConstructor会生成一个包含所有变量，同时如果变量使用了NotNull annotation ， 会进行是否为空的校验， 全部参数的构造函数的自动生成，该注解的作用域也是只有在实体类上，参数的顺序与属性定义的顺序一致

　　@Slf4j:  默认使用slf4j的日志对象

@Slf4j使用示例：

@RequestMapping(value = "/test", method = { RequestMethod.GET, RequestMethod.POST })
	@ResponseBody
	public String getAllAccounts() throws Exception {
		log.warn("lombok slf4j日志测试==================");
		return "success";
	}

测试接口输出日志：

2018-07-20 15:27:29.606  WARN 18256 --- [nio-8088-exec-1] c.o.e.controller.AccountController       : lombok slf4j日志测试==================