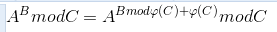K - Super A^B mod C
Given A,B,C, You should quickly calculate the result of A^B mod C. (1<=A,C<=1000000000,1<=B<=10^1000000).
Input
There are multiply testcases. Each testcase, there is one line contains three integers A, B and C, separated by a single space.
Output
For each testcase, output an integer, denotes the result of A^B mod C.
Sample Input
3 2 4
2 10 1000
Sample Output
1
24
这题的b非常大,只能用字符串处理;
需要一个降幂公式
然后带入欧拉公式,快速幂,快速乘法就可以了
#include<iostream>
#include<stdio.h>
#include<stdlib.h>
#include<cmath>
#include<string.h>
#include<algorithm>
#define sf scanf
#define pf printf
#define pb push_back
#define mm(a,b) memset((a),(b),sizeof(a))
#include<vector>
typedef __int64 ll;
typedef long double ld;
//const ll mod=1e9+7;
using namespace std;
const double pi=acos(-1.0);
vector<int>v;
char x[1000005];
ll multi(ll a,ll b,ll c)//快速乘
{
ll ans=0;
while(b)
{
if(b&1)
ans=(ans+a)%c;
a=(a+a)%c;
b>>=1;
}
return ans;
}
ll pow(ll a,ll b,ll c)//快速幂
{
ll ans=1,bas=a;
while(b)
{
if(b&1)
ans=multi(ans,bas,c);
bas=multi(bas,bas,c);
b>>=1;
}
return ans;
}
ll p[1000100];
ll ola(ll n){ //欧拉函数
ll i, j, r, aa;
r = n;
aa = n;
mm(p,0);
for(i=2; i<=sqrt(n); i++)
{
if(aa%i==0)
{
r = r/i*(i-1);
while(aa%i==0)
aa /= i;
}
}
if(aa>1)
r = r/aa*(aa-1);
return r;
}
int main()
{
ll a,b,mod;
while(~sf("%I64d %s %I64d",&a,&x,&mod))
{
ll cas=ola(mod);
ll ans=0;
int num=strlen(x);
for(int i=0;i<num;i++)//求那个b%phi(c)
{
ans=ans*10+x[i]-48;
ans%=cas;
}
if(ans<0) ans+=mod;
pf("%I64d\n",pow(a,ans+cas,mod));
}
}
K - Super A^B mod C的更多相关文章
- fzou 1759 Super A^B mod C
Problem 1759 Super A^B mod CAccept: 456 Submit: 1488Time Limit: 1000 mSec Memory Limit : 32768 ...
- FZU 1759 Super A^B mod C 指数循环节
Problem 1759 Super A^B mod C Time Limit: 1000 mSec Memory Limit : 32768 KB Problem Description G ...
- FOJ ——Problem 1759 Super A^B mod C
Problem 1759 Super A^B mod C Accept: 1368 Submit: 4639Time Limit: 1000 mSec Memory Limit : 32 ...
- FZU Super A^B mod C(欧拉函数降幂)
Problem 1759 Super A^B mod C Accept: 878 Submit: 2870 Time Limit: 1000 mSec Memory Limit : 327 ...
- Super A^B mod C
Given A,B,C, You should quickly calculate the result of A^B mod C. (1<=A,C<=1000000000,1<=B ...
- Super A^B mod C (快速幂+欧拉函数+欧拉定理)
题目链接:http://acm.fzu.edu.cn/problem.php?pid=1759 题目:Problem Description Given A,B,C, You should quick ...
- FZU:1759-Problem 1759 Super A^B mod C (欧拉降幂)
题目链接:http://acm.fzu.edu.cn/problem.php?pid=1759 欧拉降幂是用来干啥的?例如一个问题AB mod c,当B特别大的时候int或者longlong装不下的时 ...
- fzu1759 Super A^B mod C 扩展欧拉定理降幂
扩展欧拉定理: \[ a^x \equiv a^{x\mathrm{\ mod\ }\varphi(p) + x \geq \varphi(p) ? \varphi(p) : 0}(\mathrm{\ ...
- 欧拉降幂公式 Super A^B mod C
Description Given A,B,C, You should quickly calculate the result of A^B mod C. (1<=A,C<=100000 ...
随机推荐
- PPPoE图解
- set,env,export,source,exec傻傻分不清楚?
https://segmentfault.com/a/1190000013356532
- Duplicate复制数据库并创建物理StandBy(pfile版本)
1设定环境如下: Primary数据库 IP 172.17.22.16 SID orcl Standby数据库 IP 172.17.22.17 SID orcl 设置提示,以区分操作的位置 prima ...
- ubuntu 定时执行任务at
安装方法: apt-get install at 使用方法: 添加 at 11:13 warning: commands will be executed using /bin/sh at> & ...
- String s = new String("xyz");产生了几个对象?
面试官Q1:请问String s = new String("xyz");产生了几个对象? 对于这个问题,老套路先上代码: public class StringTest { pu ...
- Python 隔离沙箱 virtualenv
我认为Python一个很大的优势就是官方网站给出的众多的软件包,几乎能帮助你实现你想要的任何功能,避免了重复开发的劳动,但是零零碎碎的包,以及每个包的各种各样的版本管理就成为了一个比较棘手的问题,因此 ...
- NeoFinder for Mac(增强型文件管理工具)破解版安装
1.软件简介 NeoFinder 是 macOS 系统上一款帮助用户管理磁盘的 Mac 工具,NeoFinder for mac 能迅速组织您的数据,无论是在外部或内部磁盘,或任何其他卷.它能记 ...
- ASP.NET中TimeSpan的用法
一.TimeSpan常量.字段 TimeSpan.MaxValue; // 10675199.02:48:05.4775807TimeSpan.MinValue; //-10675199.02:48: ...
- Appium 输入 & 符号,实际输入&-
2018-10-11 12:27:12:178 - [debug] [MJSONWP] Calling AppiumDriver.setValue() with args: [["& ...
- appium 获取android 粘贴板上的内容
appium 新版本增加了获取粘贴板的内容.如果使用appium旧版本,获取粘贴板的内容不是那么容易的,甚至百度谷歌各种搜,都无法找到合适的解决方法.新版本获取android 粘贴板内容就显得很容易了 ...