leetcode每日一题：数组美丽值求和

引言

​ 今天的每日一题原题是2278. 字母在字符串中的百分比，直接模拟，逐个匹配，统计letter在原始字符串s中出现的次数，然后再计算所占百分比即可。更换成前几天遇到的更有意思的一题来写这个每日一题。

题目

2012. 数组美丽值求和

给你一个下标从 0 开始的整数数组 nums 。对于每个下标 i（1 <= i <= nums.length - 2），nums[i] 的 美丽值 等于：

• 2，对于所有 0 <= j < i 且 i < k <= nums.length - 1 ，满足 nums[j] < nums[i] < nums[k]
• 1，如果满足 nums[i - 1] < nums[i] < nums[i + 1] ，且不满足前面的条件
• 0，如果上述条件全部不满足

返回符合 1 <= i <= nums.length - 2 的所有 nums[i] 的 美丽值的总和 。

示例 1：

输入：nums = [1,2,3]
输出：2
解释：对于每个符合范围 1 <= i <= 1 的下标 i :
- nums[1] 的美丽值等于 2

示例 2：

输入：nums = [2,4,6,4]
输出：1
解释：对于每个符合范围 1 <= i <= 2 的下标 i :
- nums[1] 的美丽值等于 1
- nums[2] 的美丽值等于 0

示例 3：

输入：nums = [3,2,1]
输出：0
解释：对于每个符合范围 1 <= i <= 1 的下标 i :
- nums[1] 的美丽值等于 0

提示：

• 3 <= nums.length <= 105
• 1 <= nums[i] <= 105

思路

​ 首先还是读懂题目，对于符合1 <= i <= nums.length - 2的下标i，美丽值可能有3种情况：

• 美丽值 = 2，对于在i位置前面的数，都严格小于nums[i]；且在i位置后面的数，都严格大于nums[i]
• 美丽值 = 1，无法满足第1种情况下，且可以满足nums[i]前面的1个数严格小于它，后面的1个数严格大于它
• 美丽值 = 0，排除上述2种情况的其他情况

​ 那么对于每个在范围内的i，我们要逐个判断美丽值：对于情况1，如果每个都去比较，判断单个i需要的时间复杂度是O(n)，整体的时间复杂度就是O(n^2)；对于情况2，只要判断前后，判断单个i的时间复杂度是O(1)；对于情况3，在上述2种情况都判断后，不再需要单独判断。

​ 由此可见，我们主要优化点在于如何快速判断情况1。构造2个辅助数组，prefixMax[]和suffixMin[]，prefixMax[i]表示下标[0, i]范围内的最大值，suffixMin[i]表示下标[i, n-1]范围内的最小值。有了这2个辅助数组后，对于位置i我们在判断是否满足情况1的时间，只要判断条件 prefixMax[i-1] < nums[i] && nums[i] < suffixMin[i+1] 即可，这样每次判断的时间复杂度会缩减到O(1)，判断范围内的i的时间复杂度是O(n)。而构建这2个辅助数组，需要分别从前往后和从后往前遍历原始数组，时间复杂度也是O(n)。这样，我们就避免了O(n^2)的时间复杂度。

​ 进一步来看，如果我们从前往后处理i的话，prefixMax[]数组不需要被创建，只要滚动维护一个prefixMax的变量，表示[0, i]范围内的最大值即可，这样，可以省下一个大小为n的数组的空间开销。同理，如果从后往前处理i的话，可以省下suffixMin[]的空间。不过，这2者不可兼得。

图解

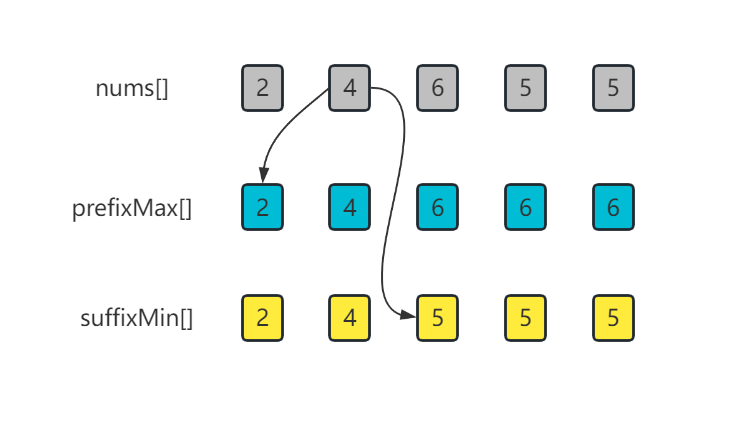
代码

class Solution {
    public int sumOfBeauties(int[] nums) {
        int[] min = getMin(nums);
        int sum = 0;
        int max = nums[0];
        for (int i = 1; i < nums.length - 1; i++) {
            if (nums[i] > max && nums[i] < min[i + 1]) {
                sum += 2;
            } else if (nums[i] > nums[i - 1] && nums[i] < nums[i + 1]) {
                sum += 1;
            }
            // 求出遍历到下一个i时，nums[0,i-1]的最大值
            max = Integer.max(max, nums[i]);
        }
        return sum;
    }

    /**
     * 从后往前，求出当前下标到数组结尾的最小值
     */
    private int[] getMin(int[] nums) {
        int n = nums.length;
        int[] min = new int[n];
        min[n - 1] = nums[n - 1];
        for (int i = n - 2; i >= 0; i-- ) {
            min[i] = Integer.min(min[i+1], nums[i]);
        }
        return min;
    }
}

耗时