模拟集成电路设计系列博客——4.1.4 二阶Gm-C滤波器

4.1.4 二阶Gm-C滤波器

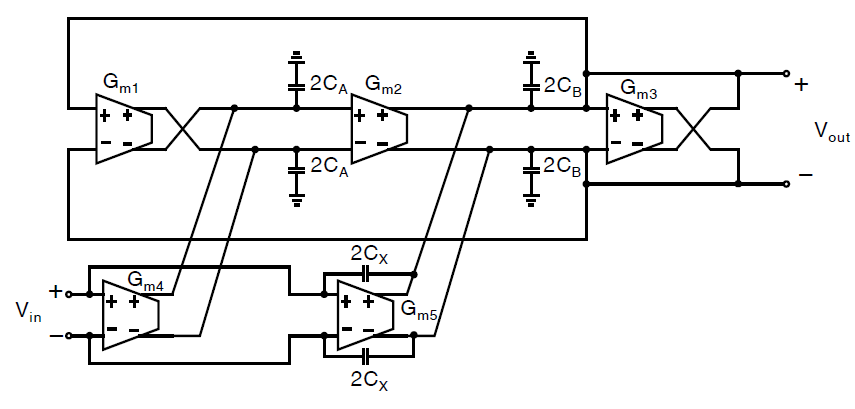
下图展示了一个全差分二阶\(G_m-C\)滤波器，其传输函数可以表达为：

\[H(s)=\frac{V_{out}(s)}{V_{in}(s)}=\frac{s^2C_X/(C_X+C_B)+sG_{m5}/(C_X+C_B)+G_{m2}G_{m4}/[C_A(C_X+C_B)]}{s^2+sG_{m3}/(C_X+C_B)+G_{m1}G_{m2}/[C_A(C_X+C_B)]} \tag{4.1.23}
\]

二阶滤波器的系统框图如下图所示：

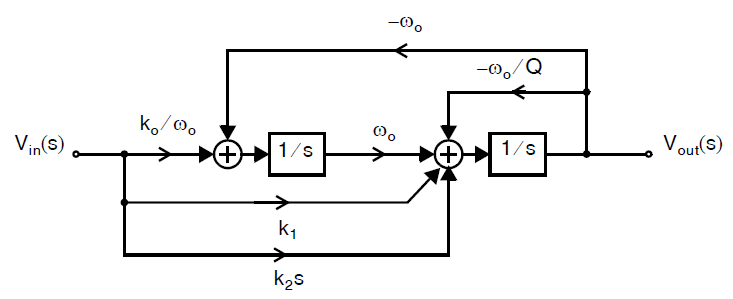
其传输函数表达为：

\[H(s)=\frac{V_{out}(s)}{V_{in}(s)}=\frac{k_2s^2+k_1s+k_0}{s^2+(\omega_0/Q)s+\omega_0^2 } \tag{4.1.24}
\]

结合\((4.1.24)\)和\((4.1.23)\)可以得到：

\[k_2 =\frac{C_X}{C_X+C_B} \tag{4.1.25}
\]

\[k_1=\frac{G_{m5}}{C_X+C_B} \tag{4.1.26}
\]

\[k_0=\frac{G_{m2}G_{m4}}{C_A(C_X+C_B)} \tag{4.1.27}
\]

以及：

\[\omega_0^2=\frac{G_{m1}G_{m2}}{C_A(C_X+C_B)} \tag{4.1.28}
\]

对于\(Q\)，我们注意到：

\[\frac{\omega_0}{Q}=\frac{G_{m3}}{C_X+C_B} \tag{4.1.29}
\]

利用\((4.1.28)\)，我们可以求出\(Q\)为：

\[Q=\sqrt{\frac{G_{m1}G_{m2}}{G_{m3}^2}\frac{C_X+C_B}{C_A}} \tag{4.1.30}
\]

利用上面的\((4.1.25)\)到\((4.1.30)\)可以推导出以下的设计方程：

\[C_X=C_B\frac{k_2}{1-k_2} \tag{4.1.31}
\]

\[G_{m1}=\omega_0 C_A \tag{4.1.32}
\]

\[G_{m2}=\omega_0(C_B+C_X) \tag{4.1.33}
\]

\[G_{m3}=\frac{\omega_0(C_B+C_X)}{Q} \tag{4.1.34}
\]

\[G_{m4}=\frac{k_0C_A}{\omega_0} \tag{4.1.35}
\]

\[G_{m5}=k_1(C_B+C_X) \tag{4.1.36}
\]

注意对于这个设计来说因子\(k_2\)存在和一阶时的\(k_1\)类似的约束，即\(0\leq k_2<1\)。

例题1：

对于一个二阶滤波器，需要有中心频率为\(20MHz\)的带通响应，\(Q\)值为5，中频增益为1，\(C_A=C_B=2pF\)，请求出所需的跨导和电容值。

解答：

带通滤波器的传输函数形式应该为：

\[H(s)=\frac{V_{out}(s)}{V_{in}(s)}=\frac{Gs\omega_0/Q}{s^2+s\omega_0/Q+\omega_0^2} \tag{4.1.37}
\]

根据中频增益为1，可以得到\(G=1\)。又根据中频\(\omega_0=2\pi \times 20MHz\)以及\(Q=5\)，我们有：

\[k_1=G\frac{\omega_0}{Q}=2.513\times 10^7 rad/s \tag{4.1.38}
\]

由于\(k_0\)和\(k_2\)为零，我们有\(C_x=G_{m4}=0\)，以及：

\[G_{m1}=\omega_0C_A=0.2513mA/V \tag{4.1.39}
\]

\[G_{m2}=\omega_0(C_B+C_X)=0.2513mA/V \tag{4.1.40}
\]

\[G_{m3}=G_{m5}=k_1C_B=50.27\mu A/V \tag{4.1.41}
\]

最后补充一下一阶和二阶滤波器的常见传输函数：

滤波器类型	传输函数
一阶低通	\(K\omega/(s+\omega)\)
一阶高通	\(Ks/(s+\omega)\)
二阶低通	\(K\omega^2/(s^2+\xi \omega s + \omega^2)\)
二阶高通	\(Ks^2/(s^2+\xi \omega s + \omega^2)\)
二阶带通	\(\xi K \omega s/(s^2+\xi \omega s + \omega^2)\)
二阶带阻	\((s^2+2\xi K_{min}\omega s+\omega^2)/(s^2+\xi \omega s + \omega^2)\)