2017蓝桥杯算式900（C++C组）

题目：算式900

小明的作业本上有道思考题：

  看下面的算式：

  (□□□□-□□□□)*□□=900

  其中的小方块代表0~9的数字，这10个方块刚好包含了0~9中的所有数字。
  注意：0不能作为某个数字的首位。

小明经过几天的努力，终于做出了答案！如下：
(5012-4987)*36=900

用计算机搜索后，发现还有另外一个解，本题的任务就是：请你算出这另外的一个解。

注意：提交的格式需要与示例严格一致；
      括号及运算符号不要用中文输入法；
      整个算式中不能包含空格。

注意：机器评卷，不要填写任何多余的内容，比如说明文字。

解析：读完本题后，我们大概有了自己的想法，每个人都有自己解决的办法，不必拘于一种做法，在这里，我分享一下我的解法。首先，根据题意，我们可以先计算出10到99内可以被900整除的所有正整数，然后利用双重for循环遍历1000到9999之间做出的差，并加以判断该差是否可以被900整除并且属于第一步结果所得集合中的元素，如果符合，则需判断最后一步：减数和被减数还有900除以差的商是否占满了0-9是个数字且无重复（在这里，本人亲自写了一个算法，学识尚浅，欢迎指教）。

代码：

#include<iostream>
#include<fstream>
#include<string>

using namespace std;

#define SUB 100                                                                //10-99以内可以被900整除的数组的下标
int A1,A2,A3,A4,B1,B2,B3,B4,C1,C2;                                //将减数被减数和900除以差的商的千百十个位数分离后的各个数
int C[SUB] = {0};                                                                //10-99以内可以被900整除的数组
int ABC[10];                                                                       //被分离后的各个数组成的集合（方便判断）

void c_init();
void abc_init();
bool is_right(int data);                                                      //遍历能被900整除的数以判断是否满足is_right_temp函数
bool is_right_temp(int m,int n,int data);                         //判断减数被减数和900除以差的商分离后的各个数字是否各不相同

int main(int argc,char** argv){

c_init();

for(int i = 0;i < 13;i++){

is_right(C[i]);
}

return 0;
} 

void c_init(){

int order = 0;

for(int i = 10;i < 100;i++){

if(900 % i == 0){

C[order] = i;
order++;
}
}
}

void abc_init(){

ABC[0] = A1;
ABC[1] = A2;
ABC[2] = A3;
ABC[3] = A4;
ABC[4] = B1;
ABC[5] = B2;
ABC[6] = B3;
ABC[7] = B4;
ABC[8] = C1;
ABC[9] = C2;
}

bool is_right(int data){

ofstream fout;
fout.open("info.txt",ios::app);
string space = "  ";

for(int i = 1000;i < 10000;i++){

for(int j = 1000;j < 10000;j++){

if(i - j == 900 / data){

if(is_right_temp(i,j,data)){

fout << "(" << i << space << "-" << space << j << ")" << space << "*" << space << data << space << "="<< space << "900" << "\n";
}
}
}
}

fout.close();
}

bool is_right_temp(int a,int b,int c){

int nums = 0;
bool jud = false;

while(a > 0){

if(a / 10 >= 100){

A4 = a % 10;

}else if(a / 10 >= 10){

A3 = a % 10;

}else if(a / 10 >= 1){

A2 = a % 10;

}else{

A1 = a;
}

a = a / 10;
}

while(b > 0){

if(b / 10 >= 100){

B4 = b % 10;

}else if(b / 10 >= 10){

B3 = b % 10;

}else if(b / 10 >= 1){

B2 = b % 10;

}else{

B1 = b;
}

b = b / 10;
}

while(c > 0){

if(c / 10 >= 1){

C2 = c % 10;

}else{

C1 = c;
}

c = c / 10;
}

abc_init();

for(int i = 0;i < 10;i++){

for(int j = 0;j < 10;j++){

if(i == ABC[j]){

jud = true;

}
}

if(jud){

nums++;
jud = false;

}

}

if(nums == 10){

return true;

}else{

return false;
}

}

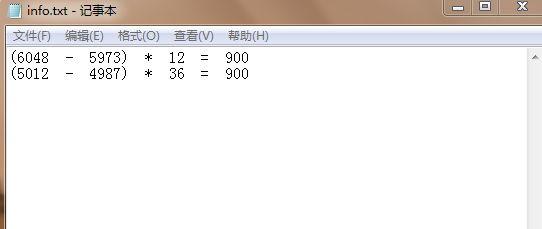
输出结果（本题本人用到了文件流知识点，也可以使用控制台输出.）