Andrew Ng - 深度学习工程师 - Part 1. 神经网络和深度学习（Week 2. 神经网络基础）

 =================第2周 神经网络基础===============

===2.1  二分分类===

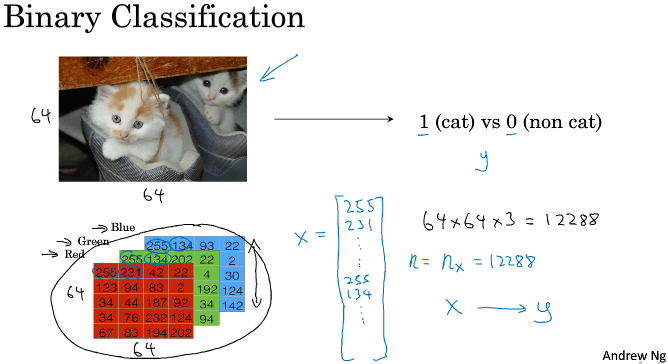
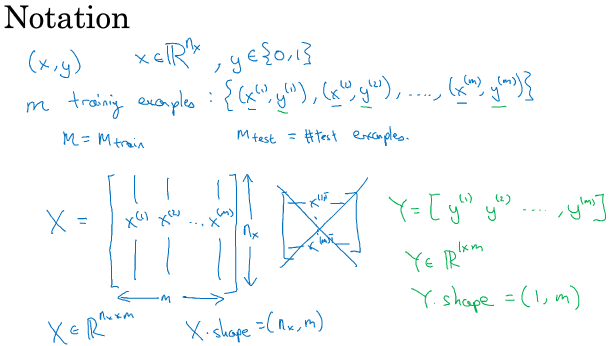
===2.2  logistic 回归===

　　It turns out, when you implement you implement your neural network, it will be easier to just keep b and w as separate parameters. 本课程中将分开考虑它们。

===2.3  logistic 回归损失函数===

　　损失函数loss func是在单个样本上定义的，而代价函数cost func它衡量在全体训练样本上的表现。其实Logistic Model 可以被看作是 一个非常小的神经网络。

 

===2.4  梯度下降法===

　　凸函数这性质是我们使用logistic回归的这个特定成本函数J的重要原因之一。通常用0来初始化<w, b>，其他初始化也ok。

　　仔细体会下图，梯度，梯度的正负，负梯度才是下降方向。也体会下，如果某点的梯度为正，那w增大，J也会增大。

 

===2.5  导数===

　　一个直观的理解是，delta_y的变化是 delta_x 的变化的 dy/dx 倍。导数的定义是你右移a 一个不可度量的无限小的值， f(a)会增加 df/da times a的改变值。

 

 

===2.6  更多导数的例子===

 

===2.7  计算图=== &

===2.8  计算图的导数计算===

　　仔细体会一下，求导的链式法则，当a改变0.001时，J改变多少，a是如何影响J的。

 

 

===2.9  logistic 回归中的梯度下降法===

 

===2.10  m 个样本的梯度下降===

　　m个样本的梯度下降的逐样本迭代版本。当你应用深度算法时，你会发现在代码中显式地使用for循环会使算法很低效。

 

===2.11  向量化===

　　下面的比较可以看出，向量化了之后快了大概 300 倍。

       

 

　　GPU和CPU都有并行化的指令，有时候会叫做SIMD指令（single instruction multiple data.），意思是如果你使用了这样的内置函数np.function or other functions that don't require you explicitly implementing a for loop. It enables Python numpy to take much better advantage of parallelism. 这点对GPU和CPU上面计算都是成立的，GPU非常擅长SIMD计算，but CPU is actually also not too bad at that. 经验法则是 只要有其他可能 就不要使用显式for循环。

 

 

===2.12  向量化的更多例子===

　　尝试用numpy内置函数代替显示loop实现你想要的功能。

 

===2.13  向量化 logistic 回归===

 

===2.14  向量化 logistic 回归的梯度输出===

 

 

===2.15  Python 中的广播===

　　Broadcasting。例子中的 cal 后面的 reshape 其实可以不用加，但当我编写Python代码时，if I'm not entirely sure what matrix, whether the dimensions of a matrix, 我会经常调用reshape命令 确保它是正确的列向量或行向量。

 

===2.16  关于 python / numpy 向量的说明===

　　注意在 In[7] 的这个数据结构中 有2个方括号，之前只有1个，So that's the difference between this is really a 1 by 5 matrix versus one of these rank 1 arrays. 

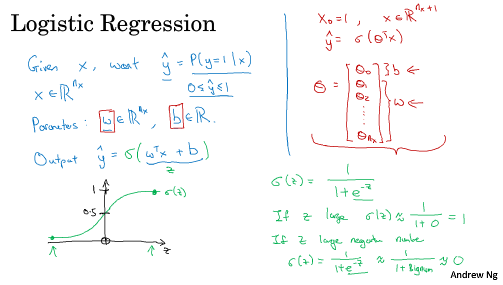
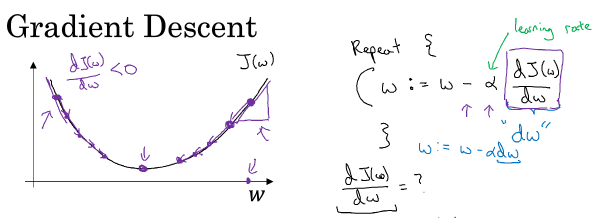
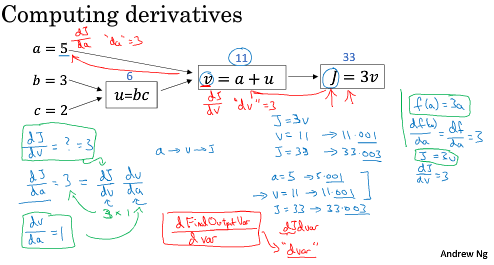
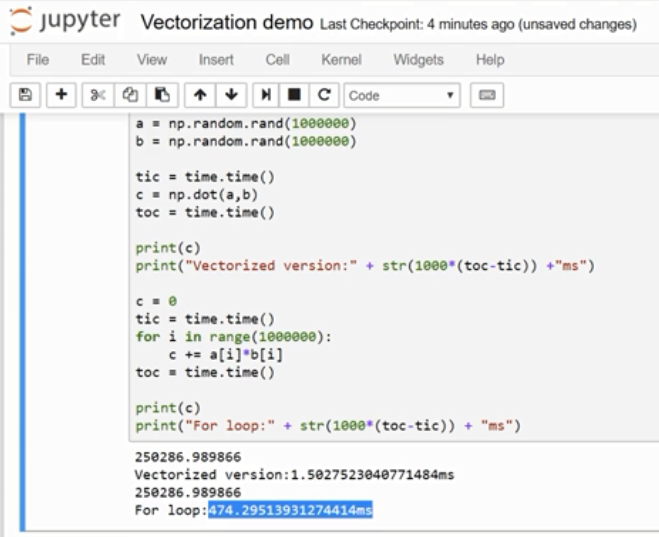
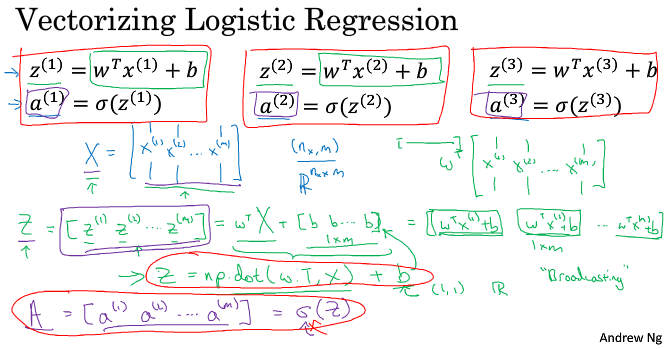
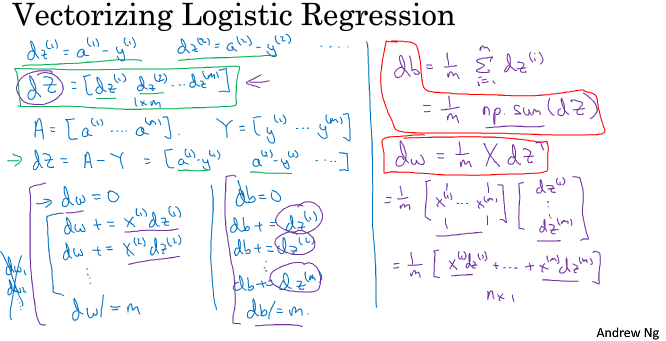
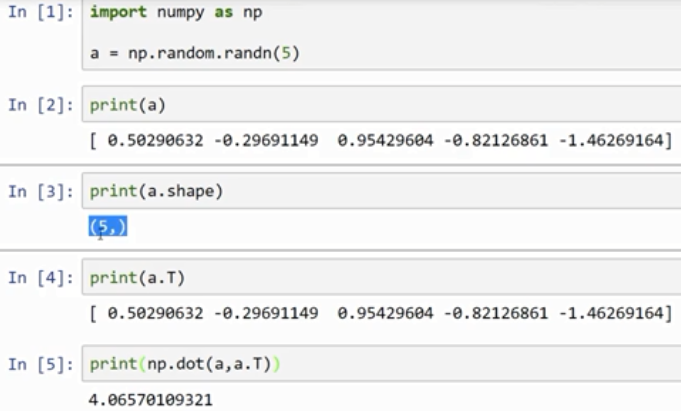
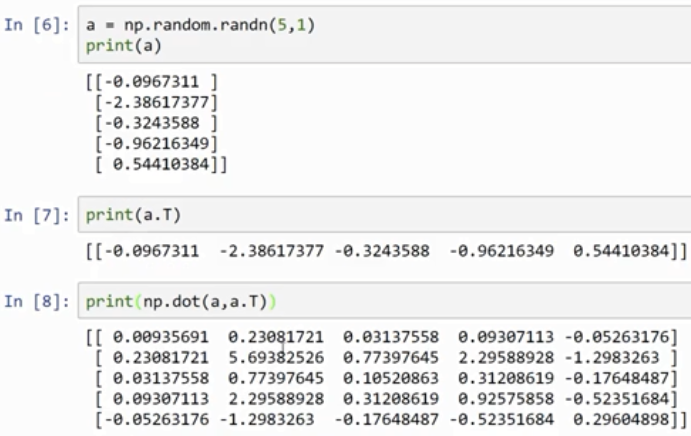
　　rank 1 array 的行为和行向量或列向量都不一样，which makes some of its effects nonintuitive. 我的建议是不要使用它们。如果某些时候确实得到了rank 1 array，你可以用reshape，使它的行为更好预测。

===2.17  Jupyter / Ipython 笔记本的快速指南===

　　使用愉快：）

 

===2.18  （选修）logistic代价函数的推导===

　　If you assume that the training examples I've drawn independently or drawn IID, then the probability of the example is the product of probabilities. 从1到m的 p(y^(i) |x^(i)）的概率乘积。