牛顿迭代法的理解与应用（ x 的平方根）

　　题目来源与LeetCode算法题中的第69题，具体内容如下（点击查看原题）：

　　　　实现 int sqrt(int x) 函数。

　　　　计算并返回 x 的平方根，其中 x 是非负整数。

　　　　由于返回类型是整数，结果只保留整数的部分，小数部分将被舍去。

　　在本题的力扣官方题解中，第一次了解牛顿法，也被称为牛顿迭代法，说实话，一开始看到题解中直接给出的公式是懵逼的，公式如下：

$x_{k+1}=\frac{1}{2}\left [ x_{k}+\frac{x}{x_{k}} \right ]$

　　主要来写一下这个公式的简要推倒过程：

　　因为不是很会Matlab，在这里借另一个题解中老哥的图一用，个人认为这张图能说明地非常清楚的：

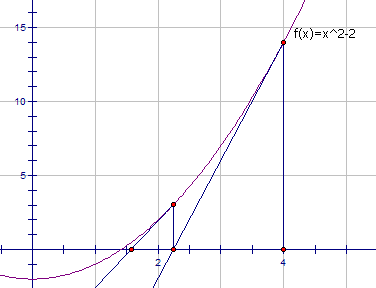
　　假设输入的值为2，则需要求解的方程即为：

$x^{2}-2=0$

　　先随便取函数上的一个点，则能表示出在这点处的切线方程，并根据此切线方程，求出此方程与 $y=0$  的交点，再根据这个交点的 $x$ 值求出原方程在这个点上的切线方程，并不断重复，可以发现，每次算得的与 $x$ 轴的交点值与实际方程的解越来越接近。当我们做更多次的循环，就能获得一个更接近实际值的解。

　　那当我们输入的值为 $a$ 时，需要求解的公式即为：

$x^{2}-a=0$

　　此时经过函数任意一点的斜率即为$2x$，设 $x$ 取值为 $x_{0}$ ，则经过 $x_{0}$ 点的切线方程可以表示为：

$y-f\left ( x_{0} \right )=2x_{0}\left ( x-x_{0} \right )$

　　根据这个方程与 $y=0$ 的交点 $x$ 则为一个更接近实际值的取值，可以表示为：

$x=x_{0}-\frac{f\left ( x_{0} \right )}{2x_{0}}$

　　当不考虑本题，一个更普适的牛顿迭代法的关系式可以表示为：

　$x_{n+1}=x_{n}-\frac{f\left ( x_{n} \right )}{f^{'}\left ( x_{n} \right )}$

　　而针对本题，将题目中的方程带入公式，就可以得出文初题解中给出的公式，即：

$x_{k+1}=\frac{1}{2}\left ( x_{k}+\frac{a}{x_{k}} \right )$

　　最后只需要根据本题的精度，设置一个满足这个精度的循环的跳出条件即可完成此题的算法实现，这里直接贴上了力扣给出的题解代码（注：原题解中少了一个return，在这里已经加上去了）：

class Solution {
  public int mySqrt(int x) {
    if (x < 2) return x;

    double x0 = x;
    double x1 = (x0 + x / x0) / 2.0;
    while (Math.abs(x0 - x1) >= 1) {
      x0 = x1;
      x1 = (x0 + x / x0) / 2.0;
    }

    return (int)x1;
  }
}