SVM之不一样的视角

在上一篇学习SVM中 从最大间隔角度出发，详细学习了如何用拉格朗日乘数法求解约束问题，一步步构建SVM的目标函数，这次尝试从另一个角度学习SVM。

回顾监督学习要素

• 数据：（\(x_i,y_i\)）

• 模型 \(\hat{y_i} = f(x_i)\)

• 目标函数（损失函数+正则项） \(l(y_i,\hat{y}_i)\)

• 用优化算法求解

SVM之Hinge Loss

• 模型

  svm要寻找一个最优分离超平面,将正样本和负样本划分到超平面两侧

\[f(x) = \bold w^\top \cdot \bold x +b
\]

• 目标函数

  \[\underset{w,b}{min}\sum^N_{i=1}max(0,1-y_i(\bold w^\top \cdot x_i+b))+\lambda ||\bold w||^2
  \]

  损失函数+正则化

• 优化算法

  梯度下降（求导时需要分段求导,见[1]）

为什么是Hinge Loss

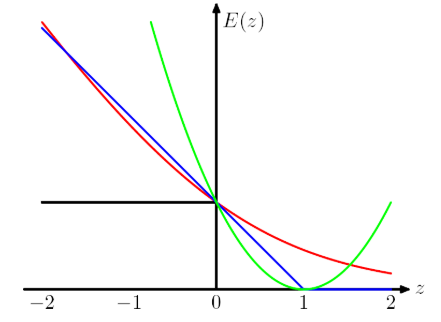
• 保持了支持向量机解的稀疏性

上图横轴 \(yf(x)>0\) 表示预测和真实标签一样，纵轴表示损失。可以看处Hinge Loss 和其他loss的区别在于，当 \(y_if(x_i) \geq 1\) 时，损失函数值为 0，意味着对应的样本点对loss没有贡献，就没有参与权重参数的更新，也就是说不参与最终超平面的决定，这才是支持向量机最大的优势所在，对训练样本数目的依赖大大减少，而且提高了训练效率。

[1] https://blog.csdn.net/oldmao_2001/article/details/95719629

[2] https://www.cnblogs.com/guoyaohua/p/9436237.html

[3] https://blog.csdn.net/qq_32742009/article/details/81432640

[4] https://www.zhihu.com/question/47746939