POJ 2671 Jimmy's Bad Day题解（很详细很友好，类似区间dp）

有问题的话欢迎在评论区提出

题意：

题目链接

你是一个送快递的，现在给你一个环，环的边有权值，代表走这条边所花的时间，每个点代表一个地点，点有点权，代表这个点上有多少货物需要你送。初始时间\(t=0\)，每到一个点，你就可以瞬间送完该点所有的货物，但每一个货物都会给你带来值为当前时间的罚款。现在你要送完所有货物，问最优情况下你的罚款最少是多少。

题解：

从样例可以看出，这题的核心就在于，快递员可以“反复横跳”，比如可以先逆时针送完一个点的货物，再掉头沿顺时针方向送完所有其它点的货物（尽管这样使得一条边经过了两次，但使得总罚款更少了）。

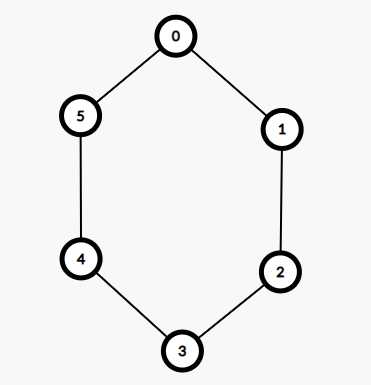
为了方便下面的说明，先约定些定义：我把起点记做0号点，0号点逆时针走\(j\)格到达的点叫做“逆时针第\(j\)点”，0号点顺时针走\(i\)格到达的点叫做“顺时针第\(i\)点”；

例如，下图中，4号点是顺时针第4点与逆时针第2点。

废话不多说，直接看状态的定义：

\(dp[i][j][0]\)：如果\(t=0\)的时候你站在顺时针\(i\)号点，送完包括端点在内，整个\([i,j]\)区间的最小罚款；

\(dp[i][j][1]\)：如果\(t=0\)的时候你站在逆时针\(j\)号点，送完包括端点在内，整个\([i,j]\)区间的最小罚款；

有两点值得注意的：

• 状态定义中假设了\(t=0\)时的位置，但事实上\(t=0\)的时候你是在起点的。为何这么假设呢？往下看就知道了；
• 上述所谓\([i,j]\)区间，表示的是由i顺时针到j的区间（划重点，也就是说，该区间走的是不含起点的那条路！），这里为了便于理解说成是\([i,j]\)，下面也用这种方式表示区间和点，不要搞混了。

那么仍以下图为例，取\(i=1\)和\(j=1\)，看看如何更新；

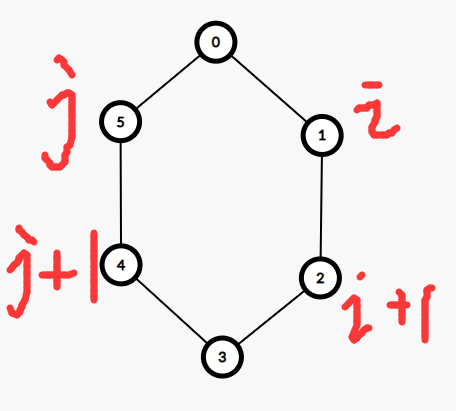
再次强调，该图里的\([i,j]\)区间是\(1,2,3,4,5\)这一段

\(dp[i][j][0]\)可以通过如下两种方式更新（特别提醒，由于\(t=0\)时你就在顺时针第\(i\)个位置，所以\(i\)处的货物不带来任何罚款，这也是下面两种情况中我们都无视了\(i\)点罚款的原因）：

• 走到\(i+1\)，这样做的花费是 : \(dp[i+1][j][0]+\)( 区间\([i+1,j]\)的货物数量之和 \(*i\)与\(i+1\)点间的时间 )
  
  解释：\(dp[i][j][0]\)假设\(t=0\)的时候你在\(i\)处，而\(dp[i+1][j][0]\)的\(t=0\)时刻假设你在\(i+1\)处，因此，两者的“开始时间”有个差距，即“\(i\)到\(i+1\)的时间”，该时间的影响是平均的作用在该区间所有货物上的。
• 掉头走到\(j\)，这样做的花费是 ： \(dp[i+1][j][1]+\)( 区间\([i+1,j]\)的货物数量之和 \(*i\)掉头走到\(j\)点的时间 )
  
  解释：与上面的情况对比，仍然是\([i+1,j]\)中的所有货物都统一的被拖延了一个时间，只不过这次该时间变成了\(i\)到\(j\)的一条路的时间

最终，\(dp[i][j][0]\)的值就取这两者与自己之间的最小值，就可以完成更新。

\(dp[i][j][1]\)的更新同理，可以参考下面dfs函数内写的方法。

后记：

最开始，我定义的\(dp[i][j][0]\)是“由\(i\)逆时针到\(j\)全部送完的最小罚款”，也就是走含起点的那一条路，相信应该会有一些人第一反应也这么想吧。但这样搞的话，似乎就没法转移了，因为你没法处理掉头多次的情况。

总之，第一反应能想到一个正确的状态，真的很重要。

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int inf=0x3f3f3f3f;
int n,num[310],len[310],lpre[310],npre[310];
int dp[310][310][2];
int nsum(int i,int j){
	int tmp=(i!=0);j=n-j;
	return npre[j]-npre[i-tmp];
}
int lsum(int i,int j){
	return lpre[j]-lpre[i];
}
int dfs(int i,int j,int pos){
	if(dp[i][j][pos]!=inf){
		return dp[i][j][pos];
	}
	if(i+j>=n){
		return dp[i][j][pos]=0;
	}
	if(pos==1){
		dp[i][j][1]=min(dp[i][j][1],dfs(i,j+1,1)+len[n-(j+1)]*nsum(i,j+1));
		dp[i][j][1]=min(dp[i][j][1],dfs(i,j+1,0)+(lpre[i]+lsum(n-j,n))*nsum(i,j+1));
	}
	else{
		dp[i][j][0]=min(dp[i][j][0],dfs(i+1,j,0)+len[i]*nsum(i+1,j));
		dp[i][j][0]=min(dp[i][j][0],dfs(i+1,j,1)+(lpre[i]+lsum(n-j,n))*nsum(i+1,j));
	}
	return dp[i][j][pos];
}
int main(){
	while(~scanf("%d",&n)){
		if(!n)	break;
		for(int i=0;i<n;i++){
			scanf("%d%d",&num[i],&len[i]);
		}
		lpre[0]=npre[0]=num[n]=0;
		for(int i=1;i<=n;i++){
			lpre[i]=lpre[i-1]+len[i-1];
			npre[i]=npre[i-1]+num[i];
		}
		memset(dp,inf,sizeof(dp));
		int ans=min(dfs(0,0,0),dfs(0,0,1));
		printf("%d\n",ans);
	}
	return 0;
}