【C语言】判断某一正整数是否为完数

什么是完数？

如果一个数等于它的因子之和，则称该数为“完数”（或“完全数”)。

例如，6的因子为1、2、3，而 6=1+2+3，因此6是“完数”。

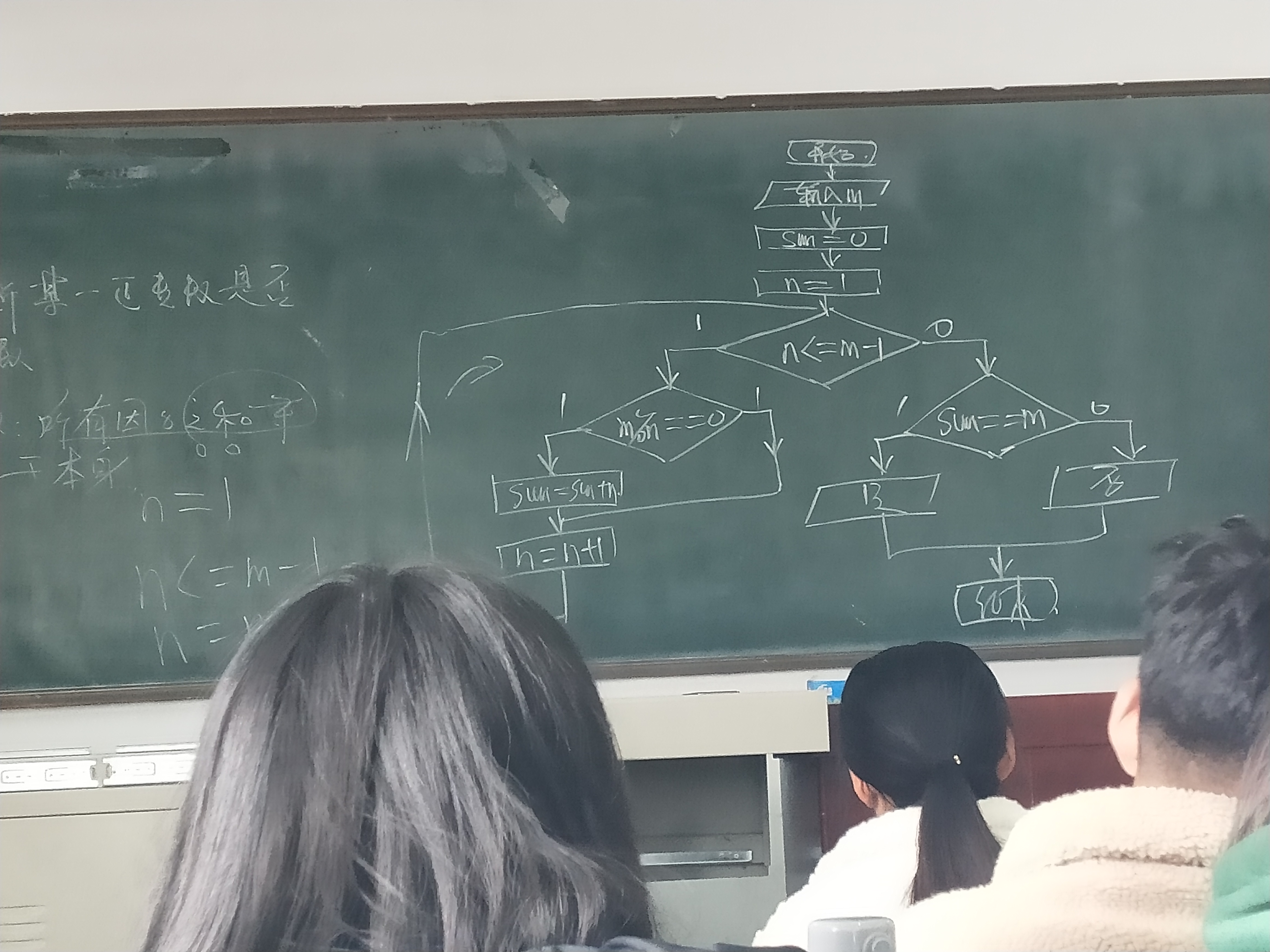
程序框图：m

 问题分析

根据完数的定义，解决本题的关键是计算出所选取的整数m（m的取值范围不固定）的因子（因子就是所有可以整除这个数的数），将各因子累加到变量sum (记录所有因子之和），若sum等于m，则可确认m为完数，反之则不是完数。

代码：

#include<stdio.h>
int main()
{
    int m, n, sum = ;
    printf("请输入一个正整数：\n");
    scanf_s("%d", &m);
    for (n = ; n < m - ; n = n + )
        if (m % n == )
            sum = sum + n;
    if (m == sum)
        printf("该数是完数\n");
    else
        printf("该数不是完数\n");
}