Chapter 3 树与二叉树
Chapter 3 树与二叉树
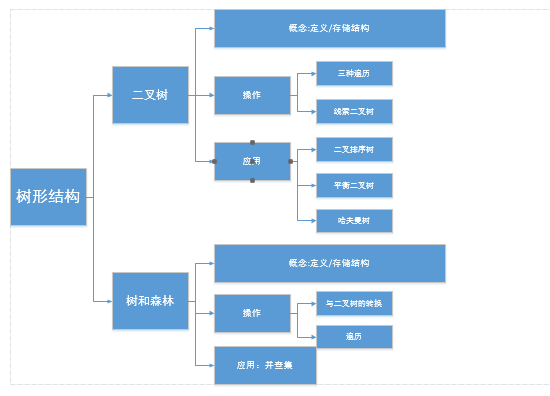
1- 二叉树
主要性质:
1 叶子结点数 = 度为2的结点数 + 1 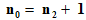
2 二叉树第i层上最多有 (i≥1)个结点
3 深度为k的二叉树最多有 个结点
2- 二叉树的链式存储结构&&遍历
1 链式存储结构
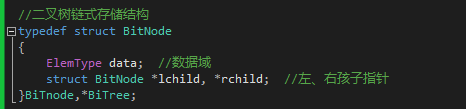
2 先序
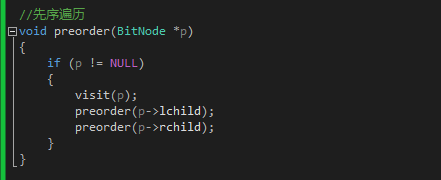
3 中序
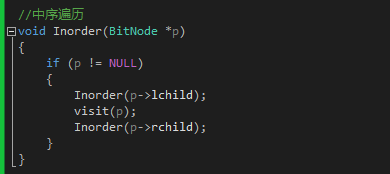
4 后序
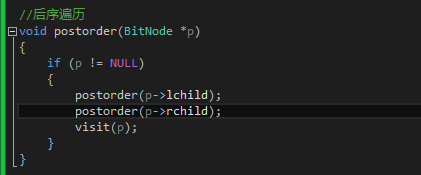
3- 线索二叉树

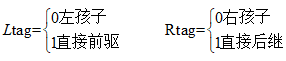
4- 树、二叉树、森林之间的转换
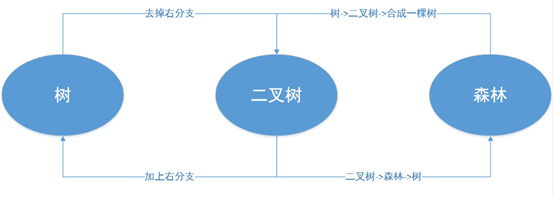
5- 树和森林的遍历

6- 树与二叉树的应用
1) 二叉排序树(查找/搜索)BST == Binary Sort/Search Tree
1 插入:一定是叶结点
2 删除:
叶子->直接删
只有一棵子树->删掉后接上子树
既有左子树,又有右子树->找到右子树最左结点/左子树最右结点代替它,然后删去。
3 查找效率分析
l 二叉排序树的ASL,主要取决于树高。
l 与二叉查找判定树相似,但二分唯一,二叉不唯一。
l 当有序表静态查找时,宜顺序表存储
l 二分查找动态查找时,宜二叉排序树
2) 平衡二叉树(AVL树)
平均查找长度ASL O(log2n)
3) 哈夫曼树(最优二叉树)
产生最短前缀码
注:
1- 树的路径长度是所有路长度的总和
Huffman的带权路径长度:根结点到任意结点的路径长度(经过的边数)与该结点上权值的乘积。
2- 二叉树与度为2的树不同。
3- 三种遍历时间复杂度O(n)
二叉排序树O(logn)
AVL树O(logn)
4- 栈:递归->非递归
队列:层次遍历
5- 先、中序/中、后序/中、层序,可唯一确定一棵二叉树
6- 前、中线索二叉树不再需要栈的支持,后序线索二叉树仍需要
7- 平衡二叉树结点递推公式
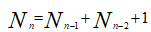
Chapter 3 树与二叉树的更多相关文章
- Java数据结构之树和二叉树(2)
从这里始将要继续进行Java数据结构的相关讲解,Are you ready?Let's go~~ Java中的数据结构模型可以分为一下几部分: 1.线性结构 2.树形结构 3.图形或者网状结构 接下来 ...
- Java数据结构之树和二叉树
从这里开始将要进行Java数据结构的相关讲解,Are you ready?Let's go~~ Java中的数据结构模型可以分为一下几部分: 1.线性结构 2.树形结构 3.图形或者网状结构 接下来的 ...
- lintcode :前序遍历和中序遍历树构造二叉树
解题 前序遍历和中序遍历树构造二叉树 根据前序遍历和中序遍历树构造二叉树. 样例 给出中序遍历:[1,2,3]和前序遍历:[2,1,3]. 返回如下的树: 2 / \ 1 3 注意 你可以假设树中不存 ...
- lintcode: 中序遍历和后序遍历树构造二叉树
题目 中序遍历和后序遍历树构造二叉树 根据中序遍历和后序遍历树构造二叉树 样例 给出树的中序遍历: [1,2,3] 和后序遍历: [1,3,2] 返回如下的树: 2 / \ 1 3 注意 你可 ...
- XJOI1559树转二叉树
树转二叉树 将一棵树转化成二叉树. 输入格式: 输入的信息,第一行一个数n,(n<=1000)是树的结点数,以下n行,第i+1行是第i个结点的信息,第一个整数,是该结点的特征数值,后列出所有孩子 ...
- 数据结构与算法系列研究五——树、二叉树、三叉树、平衡排序二叉树AVL
树.二叉树.三叉树.平衡排序二叉树AVL 一.树的定义 树是计算机算法最重要的非线性结构.树中每个数据元素至多有一个直接前驱,但可以有多个直接后继.树是一种以分支关系定义的层次结构. a.树是n ...
- python数据结构之树和二叉树(先序遍历、中序遍历和后序遍历)
python数据结构之树和二叉树(先序遍历.中序遍历和后序遍历) 树 树是\(n\)(\(n\ge 0\))个结点的有限集.在任意一棵非空树中,有且只有一个根结点. 二叉树是有限个元素的集合,该集合或 ...
- 数据结构与算法(C/C++版)【树与二叉树】
第六章<树与二叉树> 树结构是一种非线性存储结构,存储的是具有"一对多"关系的数据元素的集合. 结点: A.B.C等,结点不仅包含数据元素,而且包含指向子树的分支.例如 ...
- K:树、二叉树与森林之间的转换及其相关代码实现
相关介绍: 二叉树是树的一种特殊形态,在二叉树中一个节点至多有左.右两个子节点,而在树中一个节点可以包含任意数目的子节点,对于森林,其是多棵树所组成的一个整体,树与树之间彼此相互独立,互不干扰,但其 ...
随机推荐
- python对urlEncode进行解码
利用python自带的urlib进行编码和解码,没有什么问题.(https://www.hustyx.com/python/) 但如果是用url编码工具(http://tool.chinaz.com/ ...
- CSIC_716_20191101【编程语言、变量、垃圾回收机制】
编程语言分类:机器语言.汇编语言.高级语言. 机器语言:机器能直接识别的程序语言或指令代码(二进制指令),勿需经过翻译,每一操作码在计算机内部都有相应的电路来完成它 汇编语言:比机器语言略高级,用英文 ...
- 【JZOJ6274】梦境
description analysis 其实可以贪心 先把区间按左端点排序,转折点也排序 扫一次转折点,把所有左端点在当前点左边的区间丢进优先队列里 按照贪心策略,对于某个转折点,一定选择右端点离它 ...
- Divide by Zero 2018 and Codeforces Round #474 (Div. 1 + Div. 2, combined)G - Bandit Blues
题意:求满足条件的排列,1:从左往右会遇到a个比当前数大的数,(每次遇到更大的数会更换当前数)2.从右往左会遇到b个比当前数大的数. 题解:1-n的排列,n肯定是从左往右和从右往左的最后一个数. 考虑 ...
- 将Form的AlphaBlend属性设置为True,之后调整Form的AlphaBlendValue属性,255为不透明,数字越小透明度越大~~~想显示文字用l
将Form的AlphaBlend属性设置为True,之后调整Form的AlphaBlendValue属性,255为不透明,数字越小透明度越大~~~想显示文字用lable就行哈~~~直接在窗体上写字就行 ...
- C# .net async await 学习
async/await简单介绍 在处理比较耗时的操作(如图片处理.数据压缩.http请求等)传统的异步方法是直接使用Thread或者Task进行操作,在复杂的应用编写中可能会出现回调的问题,因此C#目 ...
- System Verilog的概念以及与verilog的对比
以下内容源自:http://blog.csdn.net/gtatcs/article/details/8970489 SystemVerilog语言简介 SystemVerilog是一种硬件描述和验证 ...
- pickle,shelve,json,configparser 的模块使用
主要内容1. 什么是序列化2. pickle3. shelve4. json5. configparser模块 一. 什么是序列化在我们存储数据或者网络传输数据的时候. 需要对我们的对象进行处理. 把 ...
- <小知识>记录
lis = [2,3,"k",["qwe",20,["k1",["tt",3,"1"]],89],& ...
- <前端>简单实现开心网注册
<!DOCTYPE html> <html lang="en"> <head> <meta charset="UTF-8&quo ...
