dp-最长公共子序列（LCS）

字符序列 与 字符字串的区别

　　序列是可以不连续的字符串 ， 字串必须要是连续的 。

问题描述 ：

　　给定两串字符串 abcde 和 acdf ， 找出 2 串中相同的字符序列，观察知 相同的字符序列为 acd 。

方法一 ： 暴力解决

　　对于一个长度为 n 的串 ， 它的字串总共有 2^n 个，在用着 2^n 个字串与另一个长度为 m 的串一一比较 ，那么复杂度为 m * 2^n 。复杂度是指数级别的，显然会超时。

方法二 ： 动态规划求解

　　两个串长度为 n 和 m ， 建一个二维数组 ， 用来记录状态 ，并且初始化数组内容为 0 ，m 和 n 分别从 0 开始 , m++ , n++ 循环

　　产生公共子序列的可能情况 ：

　　两个序列 s1~sn 和 t1 ~ tm ， 当 s i+1 == t i+1 时 ， 在s1 ~ si 和 t1 ~ ti 的公共子序列末尾追加 s i+1 。

　　s1~si 和 t1~ti+1的公共序列。

　　s1~si+1 和 t1 ~ ti 的公共序列 。

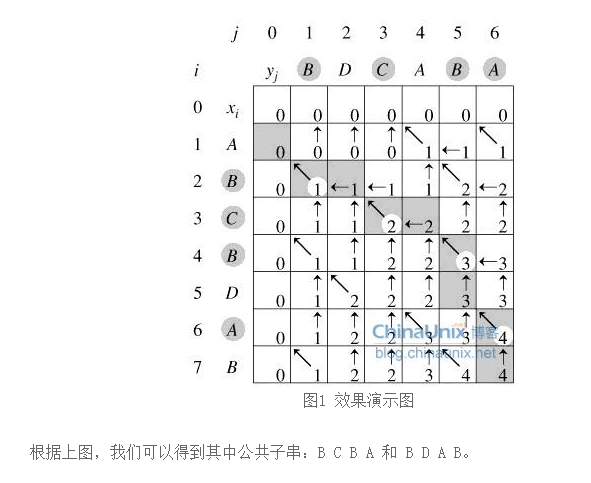
代码示例 ：

　　

/*
 * Author:  renyi
 * Created Time:  2017/8/31 8:33:36
 * File Name: 1.cpp
 */
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <string>
#include <vector>
#include <stack>
#include <queue>
#include <set>
#include <time.h>
using namespace std;
const int maxint = -1u>>1;
#define Max(a,b) a>b?a:b
#define Min(a,b) a>b?b:a
#define ll long long

int dp[10][10];

int main() {
    char a[] = "abcdegghh";
    char b[] = "cdefgh";

    int len1 = strlen(a);
    int len2 = strlen(b);

    for(int i = len1; i > 0; i--){
        a[i] = a[i-1];
    }
    for (int i = len2; i > 0; i--){
        b[i] = b[i-1];
    }

    for(int i = 1; i <= len1; i++){
        for(int j = 1; j <= len2; j++){
            if (a[i] == b[j]){
                dp[i][j] = dp[i-1][j-1]+1;
            }
            else dp[i][j] = Max(dp[i-1][j], dp[i][j-1]);
        }
    }
   // printf("%d\n", dp[len1][len2]); // 公共字串的长度

 /*   for (int i = len1, j = len2; i > 0 && j > 0; ){ // 输出公共字串
        if (a[i] == b[j]) {
            printf("%c\t", a[i]);
            i-- , j--;
        }
        else if(dp[i][j-1] >= dp[i-1][j]) j--;
        else i--;
    }

*/  int i = len1 , j = len2;
    while (i && j) {
        if ( a[i] == b[j]){
            printf("%c\t" , a[i]);
            i-- , j--;
        }
        else if (dp[i][j-1] >= dp[i-1][j]) j--;
        else i--;
    }
    return 0;
}