20172302 《Java软件结构与数据结构》第一周学习总结
2018下半年学习总结博客总目录:[第一周](https://www.cnblogs.com/hzy0628/p/9606767.html)
教材学习内容总结
第一章 概述
1.软件质量
软件工程(Software Engineering)是一门关于高质量软件开发的技术和理论的学科。
软件质量从以下八个方面进行考虑:
- 正确性 按照需求规范所规定的那样处理问题,在很大程度上满足其特定需求
- 一、程序语法错误。
- 二、程序对于几组输入数据能够得出满足需要的结果。
- 三、程序对于精心选择的、典型、苛刻切带有刁难性的几组输入数据能够得出满足要求的结果。
- 四、程序对于一切合法的输入数据都能得到满足要求的结果。
- 可靠性 应尽可能减少发生故障的频率,同时降低发生故障时所造成的损失
- 健壮性 在异常的状态能够对异常进行处理,而非发生异常就造成终止 。当输入的数据非法时,算法应当恰当的做出反应或进行相应处理,而不是产生莫名其妙的输出结果。并且,处理出错的方法不应是中断程序执行,而是应当返回一个表示错误或错误性质的值,以便在更高的抽象层次上进行处理。
- 可用性 软件的使用过程中的难易程度
- 可维护性 对软件部分代码进行修改的难易程度
- 可重用性 软件组件可重用于其他软件系统开发的难易程度
- 可移植性 软件组件在不同计算机环境下使用的难易程度
- 运行效率 在不浪费资源的情况下软件完成其目标的程度
2.数据结构
数据结构:把多个数据按照一定的存储方式,存储起来,称存储方式之为数据结构.
数据的存储方式有很多,数组,队列,链表,栈,哈希表等等. 不同的数据结构,性能是不一样的,比如有的插入比较快,查询比较快,但是删除比较慢. 有的删除比较快,插入比较快,但是查询比较慢. 根据实际操作,合理选择即可.

不同数据结构之间比较
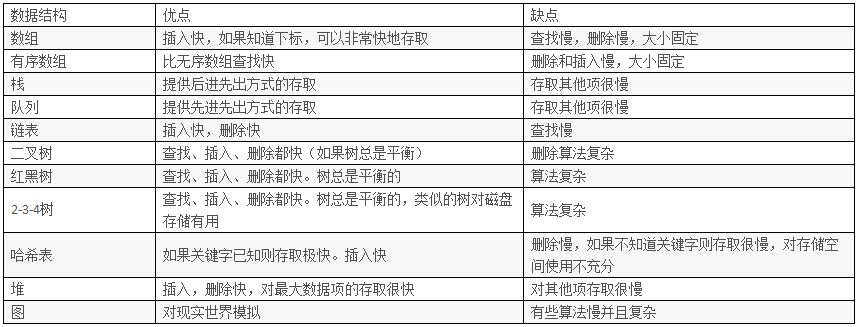
第二章 算法分析
算法分析(analysis of algorithm)是计算机科学的基础,它是从效率角度对算法进行分类。
算法效率通常用CPU的使用时间来表示。
增长函数与大O记法
增长函数是表示问题(n)大小与我们希望最优化的值之间的关系,该函数表示了该算法的时间复杂度或空间复杂度。
渐进复杂度(asymptotic complexity)称为算法的阶次,随着问题大小的增加时增长函数的一般性质,这一性质取决于该表达式的主项,即n增加时表达式中增长最快的那一项。
大O记法:我们将算法具有阶次为n的时间复杂度,记为O(n)。

增长函数的比较
- 在给定时间内系统所能处理的最大问题,我们将处理器的速度提高10倍,这时再有系统所能处理的最大问题,见下表
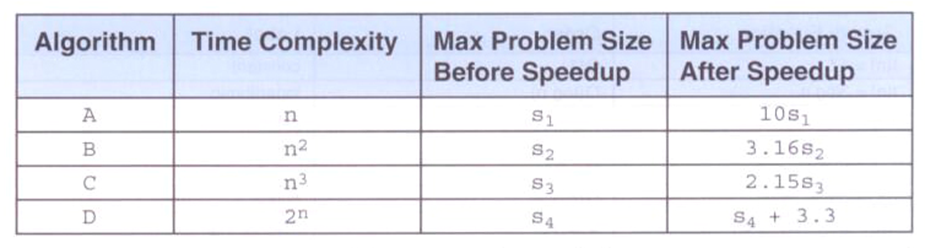
各种增长函数之间的比较
- n 较小时

- n 较大时
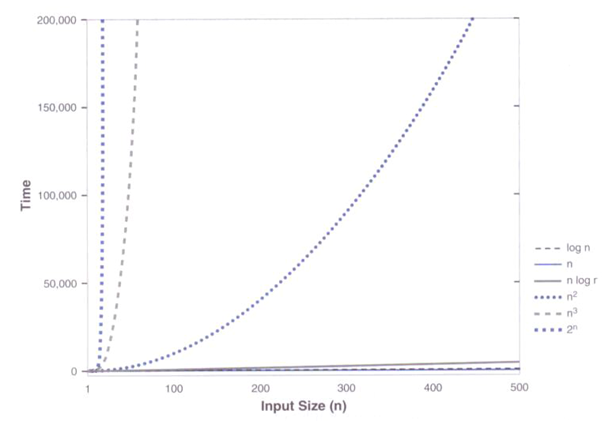
- n 较小时
结论:c(常量)<㏒₂n < n < n㏒₂n < n²< n³ < 2ⁿ < 3ⁿ< n!
时间复杂度分析
- 1.循环运行的复杂度分析
首先确定循环体的阶n,然后乘以循环执行的次数
for (int count = 0; count < n; count++)
{
// 复杂度为O(1)的步骤系列
}
n * O(1) →O(n)
- 2.嵌套循环的复杂度分析
循环出现嵌套时,循环的复杂度等于内层循环的复杂度乘以外层循环的复杂度
for (int count = 0; count < n; count++)
for (int count2 = 0; count2 < n; count2++)
{
//复杂度为O(1)步骤系列
}
内外层循环的复杂度均为O(n),整体的复杂度为O(n²)
- 3.方法调用的复杂度分析
循环体可能包含方法的调用,要确定循环体的阶,需要考虑调用方法的阶
for (int count=0 ; count<n; count++)
{
Printsum(count);
}
以下是Printsum方法
Public void printsum(int count)
{
Int sum =0;
for(int i=0; i<count; i++)
sum += i;
System.out.println(sum);
}
于是整体的复杂度为O(n²)
时间复杂度的计算规则
- 加法规则
T(n,m) = T1(n) + T2(n) = O (max ( f(n), g(m) )
- 加法规则
- 乘法规则
T(n,m) = T1(n) * T2(m) = O (f(n) * g(m))
- 乘法规则
- 一个特例(问题规模为常量的时间复杂度)
在大O表示法里面有一个特例,如果T1(n) = O(c), c是一个与n无关的任意常数,T2(n) = O ( f(n) ) 则有T(n) = T1(n) * T2(n) = O ( c*f(n) ) = O( f(n) )。也就是说,在大O表示法中,任何非0正常数都属于同一数量级,记为O(1)。
- 一个特例(问题规模为常量的时间复杂度)
教材学习中的问题和解决过程
可靠性与健壮性之间的关系是什么?
可靠性关注的是软件发生故障的频率以及在什么环境下发生故障,而健壮性关注的是软件系统出现故障会发生什么?
系统的健壮性(robustness)也称为系统的坚固性或坚实性,这是衡量一个系统能否从各种出错条件下恢复能力的一种测度。引起出错的条件可以是来自系统内部,也可以是系统外部的。比如:一个健壮的系统可以容许数据输入的错误,也可以允许内部组成部件的故障。虽然在健壮性与可靠性之间有着一定的联系,但是两者是不同的测度。
课后练习题解答
EX2.1 下列增长函数的阶次是多少?
a.10n^2+100n+1000 n^2
b.10n^3-7 n^3
c.2n+100n3 2^n
d.n^2 ·log(n) n^2 ·log(n)EX2.4 请确定下面代码段的增长函数和阶次
for(int count = 0 ; count < n ; count++)
for(int count2 = 0 ; count2 < n ; count2 = count2 + 2)
{
System.out.println(count,count2);
}
}
如题,内层循环是n/2,外层循环是n,故增长函数f(n) = n^2 /2,则阶次是O(n^2)。
- EX 2.5 请确定下面代码段的增长函数和阶次
for(int count = 0 ; count < n ; count++)
for(int count2 = 1 ; count2 < n ; count2 = count2 * 2)
{
System.out.println(count,count2);
}
}
如题,内层循环次数为log(2)n,外层循环次数n,所以增长函数是nlog(2)n,而阶次只与增长函数的最高阶项有关,忽略次项与常数项,故阶次是O(nlog2n)。
结对及互评
- 本周结对学习情况
博客中值得学习的或问题: 课后练习题完成很认真,解析也比较详细,教材内容总结可增加些内容,侧重对知识的理解部分。
结对学习内容:学习第一章及第二章。
其他(感悟、思考等)
感悟
- 第一周的学习任务比较轻松,学习内容也比较简单。又到了一个新的起点,希望能够保持最开始的状态去学完这一学年,完成好这门课程。
参考资料
20172302 《Java软件结构与数据结构》第一周学习总结的更多相关文章
- 《JAVA程序设计》_第一周学习总结
20175217吴一凡 <java程序设计> 第一周学习总结 虽然已经做好了心理准备,但第一周的学习任务着实让我忙了整整三天,还是挺充实的吧.寒假已经在自己的电脑上安装好了虚拟机,我就在我 ...
- 201521145048《Java程序设计管理》第一周学习总结
1. 本周学习总结 学习并了解Java的发展与历史 在网上视频中学习Java 了解并区分JVM JRE JDK 将java与已学语言做比较,发现相同处 2. 书面作业 Q1.为什么java程序可以跨平 ...
- 20172329 2018-2019《Java软件结构与数据结构》第一周学习总结
2018-2019-20172329 <Java软件结构与数据结构>第一周学习总结 在这学期就已经大二了,也已经步入了学习专业课的核心时间,在这个阶段,我们应该了解自己的学习情况,针对自己 ...
- 20172328 2018-2019《Java软件结构与数据结构》第一周学习总结
20172328 2018-2019<Java软件结构与数据结构>第一周学习总结 概述 Generalization 本周学习了软件质量.数据结构以及算法分析的具体内容,主要依托于所用教材 ...
- 《JAVA软件结构与数据结构》第一周学习总结
学号 20172326 <JAVA软件结构与数据结构>第一周学习总结 教材学习内容总结 软件质量的几大特性 增长函数与大O记法 大O记法用来表示表示增长函数,从而来表示算法的复杂度 算法的 ...
- 20172305 2018-2019-1 《Java软件结构与数据结构》第一周学习总结
20172305 2018-2019-1 <Java软件结构与数据结构>第一周学习总结 教材学习内容总结 本周内容主要为书第一章和第二章的内容: 第一章 软件质量: 正确性(软件达到特定需 ...
- 20172328 2018—2019《Java软件结构与数据结构》第二周学习总结
20172328 2018-2019<Java软件结构与数据结构>第二周学习总结 概述 Generalization 本周学习了第三章集合概述--栈和第四章链式结构--栈.主要讨论了集合以 ...
- 20172328 2018-2019《Java软件结构与数据结构》第三周学习总结
20172328 2018-2019<Java软件结构与数据结构>第三周学习总结 概述 Generalization 本周学习了第五章:队列.主要内容包含队列的处理过程.如何用对例如求解问 ...
- 20172328 2018-2019《Java软件结构与数据结构》第五周学习总结
20172328 2018-2019<Java软件结构与数据结构>第五周学习总结 概述 Generalization 本周学习了第九章:排序与查找,主要包括线性查找和二分查找算法和几种排序 ...
- 20172328 2018-2019《Java软件结构与数据结构》第六周学习总结
20172328 2018-2019<Java软件结构与数据结构>第六周学习总结 概述 Generalization 本周学习了第十章:非线性集合与数据结构--树.主要讨论了树的使用和实现 ...
随机推荐
- mac安装mysql8.0的错误
在MySQL 8.0中,caching_sha2_password是默认的身份验证插件,而不是mysql_native_password.有关此更改对服务器操作的影响以及服务器与客户端和连接器的兼容性 ...
- 04-Bootstrap的插件
1.下拉菜单 代码如下: <div class="dropdown"> <button class="btn btn-default dropdown- ...
- Spring_使用XML文件的方式配置事务
步骤: 正常配置jdbctemplate 正常配置bean 配置事物管理器 配置事物管理器 配置aop切入点,通过切入点把事物链接起来 思路: 接着上一个买书的例子吧,直接拷到新包下,把注解都干掉,需 ...
- FineReport——获取控件值和单元格值
设置单元格的值(填报预览): //contentPane.setCellValue(1,0,"abc");//参数面板给单元格赋实际值,即可填报 contentPane.curLG ...
- Python-JS事件与面向对象操作
目录一.函数高级 循环绑定: 使用循环绑定会出现的问题及解决方案: 二.面向对象 3.构造函数(ES5) 三.JS选择器 1.getElement系列(最严谨) 2.querySelector系列(最 ...
- Oracle 高级排序函数 和 高级分组函数
高级排序函数: [ ROW_NUMBER()| RANK() | DENSE_RANK ] OVER (partition by xx order by xx) 1.row_number() 连续且递 ...
- python抓取bing主页背景图片
最初Python2写法: #!/usr/bin/env python # -*- coding:utf-8 -*- # -*- author:nancy -*- # python2抓取bing主页所有 ...
- 打开MSSQL 2008 R2的时候,展开数据库都显示以下的错误提示: 值不能为空。参数名viewinfo(microsoft.sqlserver.management.sqlstudio.explorer)
打开MSSQL 2008 R2的时候,展开数据库都显示以下的错误提示: 值不能为空.参数名viewinfo(microsoft.sqlserver.management.sqlstudio.explo ...
- System.getenv()和System.getProperty() 的区别
1.System.getenv() 方法是获取指定的环境变量的值.它有两种方法,一种是接收参数为任意字符串,当存在指定环境变量时即返回环境变量的值,否则返回null.另外一种是不接受参数,那么返回的是 ...
- [转] webpack3.0踩坑:postcss-loader的使用
解决方案: 只是换了一种引入方式,解决了 1,创建postcss.config.js文件,添加如下代码:(引入autoprefixer插件) 1 2 3 4 module.exports = { ...
