Box-Muller 与 ziggurat

1. Ziggurat 算法与 Box-muller 算法的效率比较

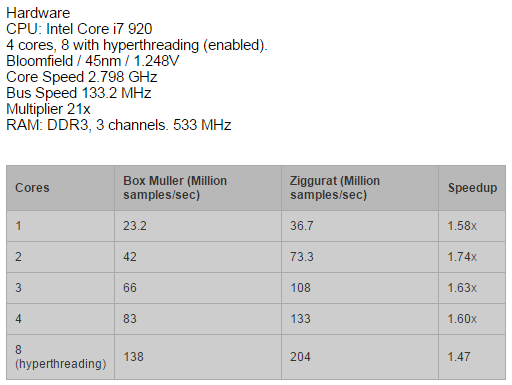
2. Box-Muller

a. 一般形式 因函数调用较多，速度慢，当u接近0时存在数值稳定性问题

先假设。

用Box-Muller方法，随机抽出两个从均匀分布的数字和。然后


那和都是正态分布的。
证明可用极坐标，请参考教科书中的Box-Muller方法。

另外使用反函数，先随机抽出一个从均匀分布的数字，然后

那是正态分布的。

b.极坐标形式，速度快且有更好的数值鲁棒性

double pf_ran_gaussian(double sigma)
{
  double x1, x2, w, r;

  do
  {
    do { r = drand48(); } while (r==0.0);
    x1 = 2.0 * r - 1.0;
    do { r = drand48(); } while (r==0.0);
    x2 = 2.0 * r - 1.0;
    w = x1*x1 + x2*x2;
  } while(w > 1.0 || w == 0.0);

  return(sigma * x2 * sqrt(-2.0*log(w)/w));
}

 3. zigurat 方法

Box–Muller 算法虽然非常快，但是由于用到了三角函数和对数函数，相对来说还是比较耗时的，如果想要更快一点有没有办法呢？

当然有，这就是 Ziggurat 算法，不仅可以用于快速生成正态分布，还可以生成指数分布等等。Ziggurat 算法的基本思想是利用拒绝采样，什么是拒绝采样呢？

拒绝采样（Rejection Sampling），有的时候也称接收 - 拒绝采样，使用场景是有些函数p(x)

太复杂在程序中没法直接采样，那么可以设定一个程序可抽样的分布q(x)比如正态分布等等，然后按照一定的方法拒绝某些样本，达到接近p(x)

分布的目的：

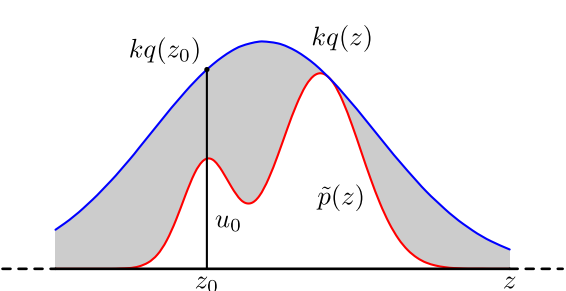
具体操作如下，设定一个方便抽样的函数 $q(x)$，以及一个常量 $k$，使得 $p(x)$ 总在 $kq(x)$ 的下方。（参考上图）

• x轴方向：从q(x)分布抽样得到a

• y轴方向：从均匀分布(0,kq(a))中抽样得到u

• 如果刚好落到灰色区域：u>p(a)，拒绝；否则接受这次抽样

• 重复以上过程

证明过程就不细说了，知道怎么用就行了，感兴趣的可以看看这个文档

• Acceptance-Rejection Method

不过在高维的情况下，拒绝采样会出现两个问题，第一是合适的 $q$ 分布比较难以找到，第二是很难确定一个合理的 $k$ 值。这两个问题会造成图中灰色区域的面积变大，从而导致拒绝率很高，无用计算增加。

采用拒绝采样来生成正态分布，最简单直观的方法莫过于用均匀分布作为 $q(x)$，但是这样的话，矩形与正态分布曲线间的距离很大，就会出现刚才提到的问题，高效也就无从谈起了。

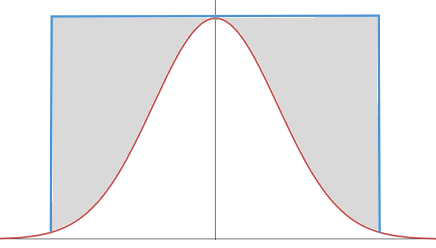
而 Ziggurat 算法高效的秘密在于构造了一个非常精妙的q(x)，看下面这张图

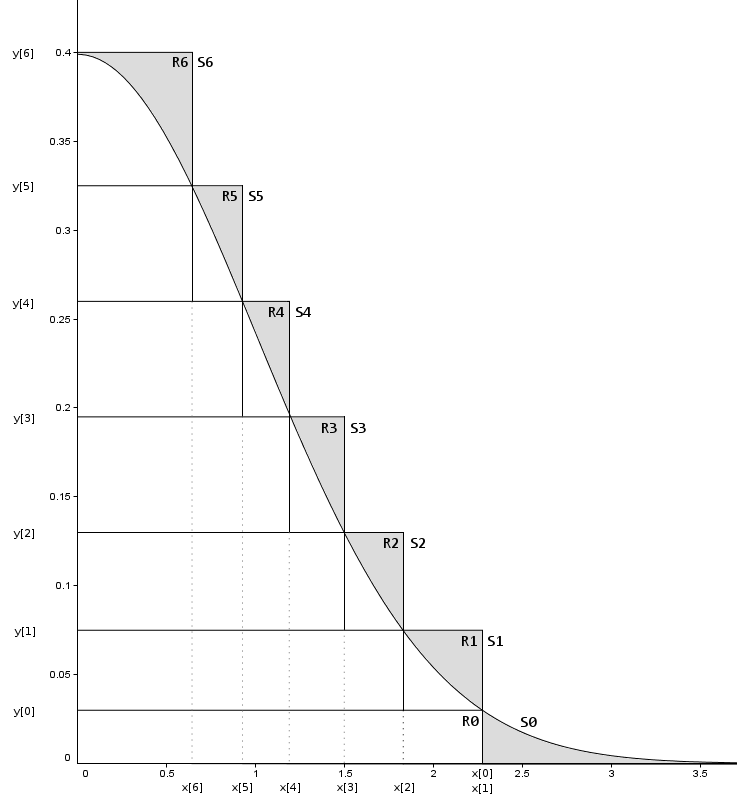
我们用多个堆叠在一起的矩形，这样保证阴影部分（被拒绝部分）的始终较小，这样就非常高效了

简单对图作一个解释：

• 我们用R[i]来表示一个矩形，R[i]的右边界为x[i]，上边界为y[i]。S[i]表示一个分割，当i=0时，S[0]=R[0]+tail，其他情况S[i]==R[i]
• 除了R[0]以外，其他每个矩形面积相等，设为定值A。R[0]的面积 = A-tail的面积。这样保证从任何一个分割中抽样(x,y)的概率相等
• 当任意选定一个R[i]在其中抽样(x,y)，若x<x[i+1]，y必然在曲线下方，满足条件，接受x；若x[i+1]<x<x[i]，则还需要进一步判断。同样这里R[0]和tail中的样本需要进行特殊处理
• 这里为了方便解释，只用了几个矩形，在程序实现的时候，一般使用128或256个矩形

可以看出，为了提高效率，Ziggurat 算法中使用了许多技巧性的东西，这在其C代码实现中更加明显，使用了与运算和字节等各种小技巧，代码就不在这里贴了，感兴趣可以看看下面几个版本，C版本的追求的是极致的速度，每个矩形的边界已经提前计算好了。C#版本中的注释非常详细，Java版的基本与C#一致，但是效率一般。

• C
• C#
• Java

4. 总结

Box-muller 算法应对一般的需求足够了，但是要生成大量服从正态分布的随机数时，Ziggurat 算法效率会更高一点。

参考： https://www.taygeta.com/random/gaussian.html    // Box-Muller的介绍

            https://cosx.org/2015/06/generating-normal-distr-variates   // 对比介绍

            https://www.zhihu.com/question/29971598