tensorflow入门(1):构造线性回归模型

今天让我们一起来学习如何用TF实现线性回归模型。所谓线性回归模型就是y = W * x + b的形式的表达式拟合的模型。

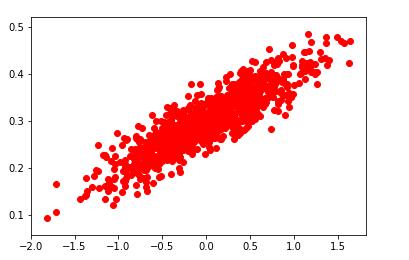
我们先假设一条直线为 y = 0.1x + 0.3，即W = 0.1，b = 0.3,然后利用随机数在这条直线附近产生1000个随机点，然后利用tensorflow构造的线性模型去学习，最后对比模型所得的W和b与真实值的差距即可。

(某天在浏览Github的时候，发现了一个好东西，Github上有一个比较好的有关tensorflow的Demo合集，有注释有源代码非常适合新手入门。)

import numpy as np     #numpy库可用来存储和处理大型矩阵
import tensorflow as tf
import matplotlib.pyplot as plt    #主要用于画图

#产生1000个随机点
num_points = 1000

vectors_set = []
for i in range(num_points):
#利用random的内置函数产生1000个符合 均值为0，标准差为0.55的正态分布
　　x1 = np.random.normal(0.0, 0.55)
　　y1 = x1 * 0.1 + 0.3 + np.random.normal(0.0, 0.03)
　　vectors_set.append([x1,y1])

x_data = [v[0] for v in vectors_set]
y_data = [v[1] for v in vectors_set]

plt.scatter(x_data, y_data, c = 'r')
plt.show()

#生成1维的W矩阵，取值为【-1，1】之间的随机数
W = tf.Variable(tf.random_uniform([1], -1.0, 1.0), name = 'W')
#生成1维的b矩阵，初始值为0
b = tf.Variable(tf.zeros([1]), name = 'b')
#经过计算得出预估值Y
y = W * x_data + b

#以预估值Y和实际值Y_data之间的均方误差作为损失
loss = tf.reduce_mean(tf.square(y - y_data), name = 'loss')

#采用梯度下降法进行优化参数(梯度下降原理详情见另一篇博客)
#optimizer = tf.train.GradientDescentOptimizera(0.5).minimize(loss)
optimizer = tf.train.GradientDescentOptimizer(0.5)

#训练的过程就是最小化这个误差值
train = optimizer.minimize(loss, name = 'train')

sess = tf.Session()

init = tf.global_variables_initializer()
sess.run(init)

#打印初始化的W和b的值
print('W = ', sess.run(W), 'b = ', sess.run(b), "loss = ", sess.run(loss))
#因为数据规模不大且符合正态分布，所以执行20次训练就能达到一定效果
for step in range(20):
　　sess.run(train)
#输出训练后的W和B
　　print('W = ', sess.run(W), 'b = ', sess.run(b), "loss = ", sess.run(loss))

实验结果如下：

1.1000个散点图

2.预测出W、b以及loss的值

W = [0.40727448] b = [0.] loss = 0.12212546
W = [0.30741683] b = [0.30278787] loss = 0.014318982
W = [0.24240384] b = [0.3016729] loss = 0.0071945195
W = [0.19786316] b = [0.30094698] loss = 0.0038506198
W = [0.16734858] b = [0.30044967] loss = 0.0022811447
W = [0.1464432] b = [0.30010894] loss = 0.001544504
W = [0.13212104] b = [0.29987553] loss = 0.0011987583
W = [0.122309] b = [0.2997156] loss = 0.0010364805
W = [0.11558682] b = [0.29960606] loss = 0.00096031476
W = [0.11098149] b = [0.29953098] loss = 0.0009245659
W = [0.1078264] b = [0.29947957] loss = 0.00090778706
W = [0.10566486] b = [0.29944435] loss = 0.00089991186
W = [0.10418401] b = [0.2994202] loss = 0.0008962157
W = [0.10316949] b = [0.29940367] loss = 0.0008944806
W = [0.10247444] b = [0.29939234] loss = 0.00089366647
W = [0.10199826] b = [0.2993846] loss = 0.00089328433
W = [0.10167204] b = [0.29937926] loss = 0.0008931049
W = [0.10144854] b = [0.29937562] loss = 0.00089302065
W = [0.10129543] b = [0.29937312] loss = 0.00089298113
W = [0.10119054] b = [0.29937142] loss = 0.0008929627
W = [0.10111867] b = [0.29937026] loss = 0.000892954

根据实验结果可以看出第20次预测出的W和b值基本符合我们之前假设直线的值