中缀表达式转后缀表达式(Java代码实现)

后缀表达式求值

后缀表达式又叫逆波兰表达式，其求值过程可以用到栈来辅助存储。例如要求值的后缀表达式为：1 2 3 + 4 * + 5 -，则求值过程如下：

1. 遍历表达式，遇到数字时直接入栈，栈结构如下

　　　　

　　2.　接着读到 “+”操作符，则将栈顶和次栈顶元素出栈与操作符进行运算，执行 2 + 3操作，并将结果5压入栈中，此时栈结构如下

　　　　

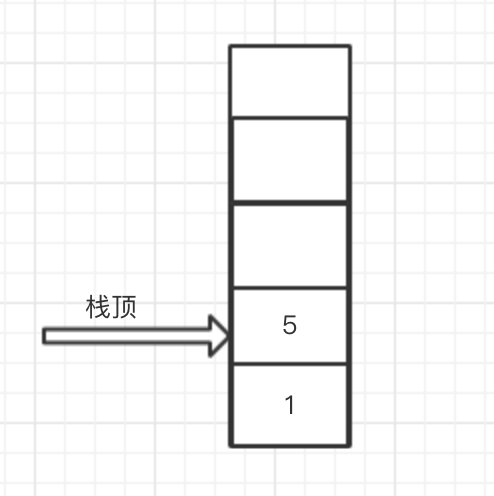
3.  继续读到4，是数字则直接压栈，此时栈结构如下

　　　　

　　4. 继续向后读取，此时读取到操作符“*”，则将栈顶和次栈顶元素出栈与操作符进行运算，即执行 5 * 4 ，然后将结果20压入栈中，此时栈结构如下

　　　　

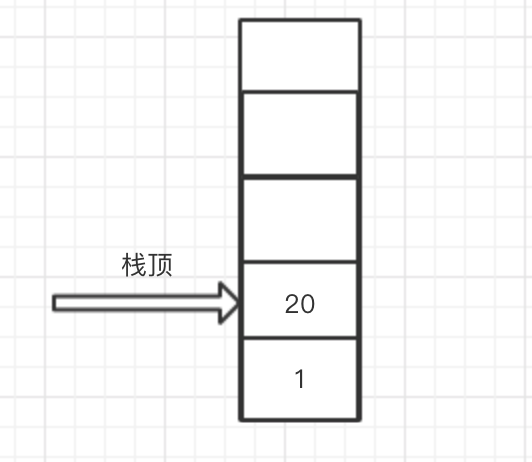
　　5. 继续向后读取，此时读到操作符“+”，则将栈顶和次栈顶元素出栈与操作符进行运算，即执行1 + 20，然后将结果21压入栈中，此时栈结构如下

　　　　

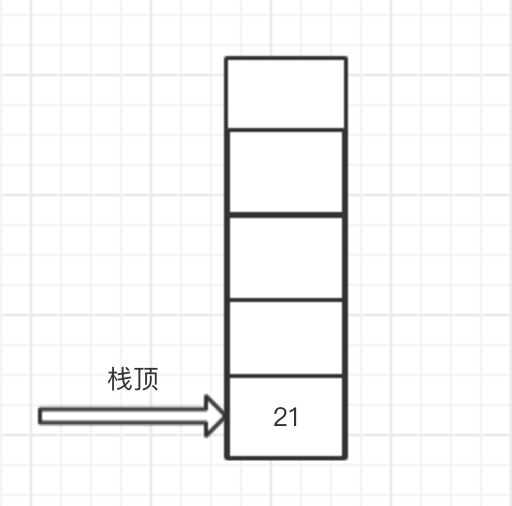
　　6. 继续向后读取，此时读到数字5，则直接将数字压栈，栈结构如下

　　　　

　　7. 读取到最后一个为操作符，将栈顶和次栈顶元素出栈与操作符进行运算，即执行 21- 5（注意顺序 次栈顶-栈顶）,然后将结果16压入栈中，此时栈结构如下

　　　　

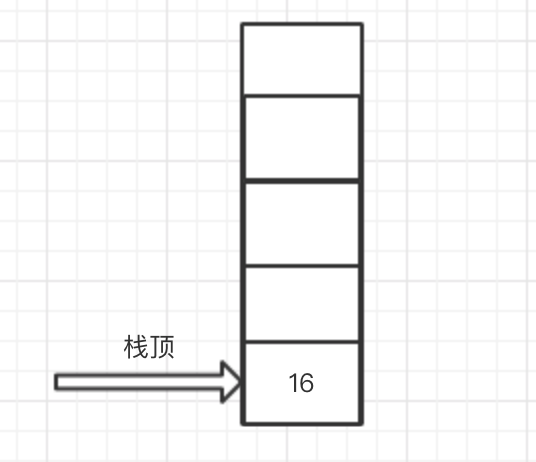
　　此时栈顶元素即为表达式的结果。（注：为方便理解，这里栈顶指针向下移动后，上面元素直接去掉了，实际情况数据还会存在对应位置，只是通过栈顶指针读取不到，等待GC）

中缀表达式转后缀表达式

中缀表达式为我们人类能识别的方式，而后缀表达式是计算机进行运算的方式（即我们上述的过程)。

转换规则

　　1）我们使用一个stack栈结构存储操作符，用一个List结构存储后缀表达式结果

　　2）首先读取到数字，直接存入list中

　　3）当读取到左括号"("时，直接压栈，当读取到运算符时，分两种情况讨论

　　　　a.当运算符栈为空或者栈顶操作符的优先级小于当前运算符优先级时(如+和-的优先级低于 * 和 /)，直接入栈

　　　　b.当运算符不为空时且栈顶操作符的优先级大于或等于当前运算符优先级时，循环执行出栈操作并加入list中，直到遇到优先级小于当前运算符的元素为止。循环执行完后再将当前运算符压栈。另外需要注意的是，只有遇到右括号时，左括号才出栈

　　4) 当遇到右括号")"时，循环执行出栈操作并加入到list中，直到遇到左括号为止。并将左括号弹出，但不加入list中

　　5) 表达式的值读取完后，将操作符栈中的所有元素弹出并加入到list中

　　执行完上面步骤后，list中存储的顺序即为我们转换后的后缀表达式的结果

转换实例

　　下面利用上面定义的转换规则，将表达式 1+((2+3)*4)-5 以图解的方式描述其转换过程

　　1.首先定义一个存储操作符的栈 Stack<String> stack = new Stack<>() ，和一个存储最终后缀表达式的列表 List<String> list = new ArrayList<>()

　　2.读取表达式，首先读取到数字 1 ，按照上述规则，直接添加至list中。此时stack和list结构如下

　　

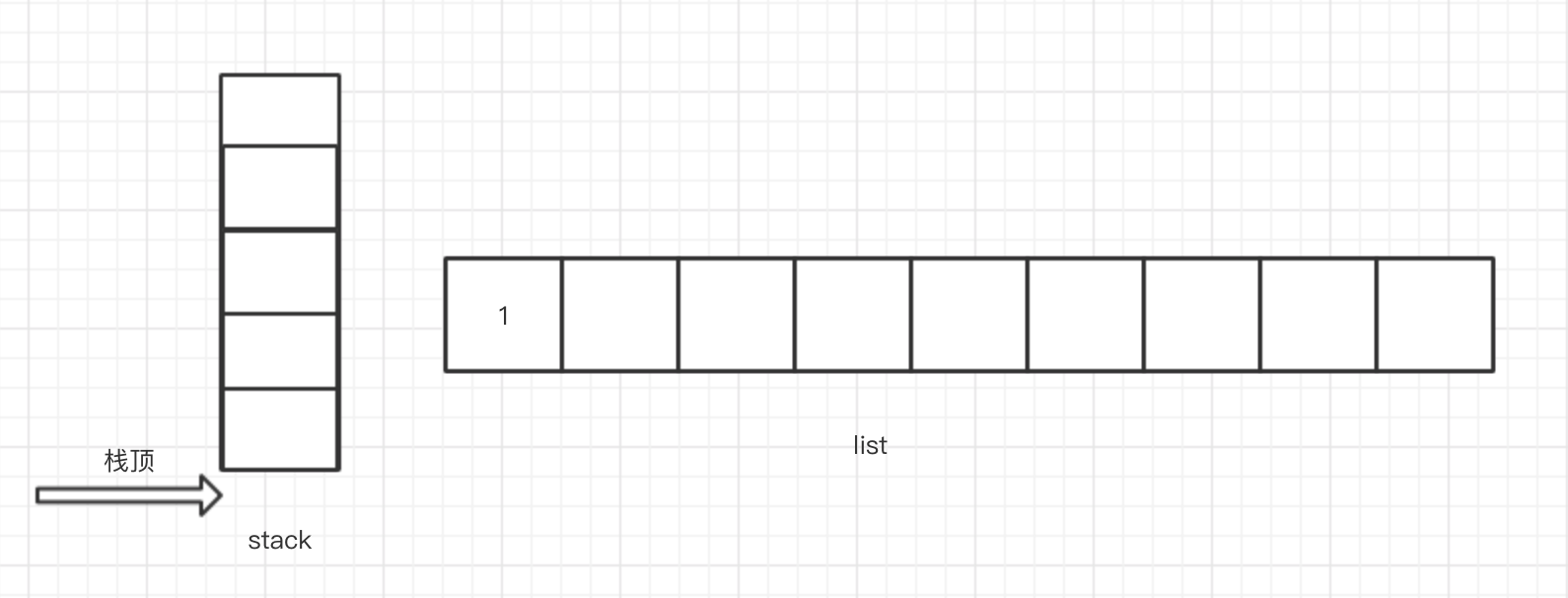
　　3.然后读取到操作符 + ，此时stack为空，按照上述规则，直接入栈，此时stack和list结构如下

　　

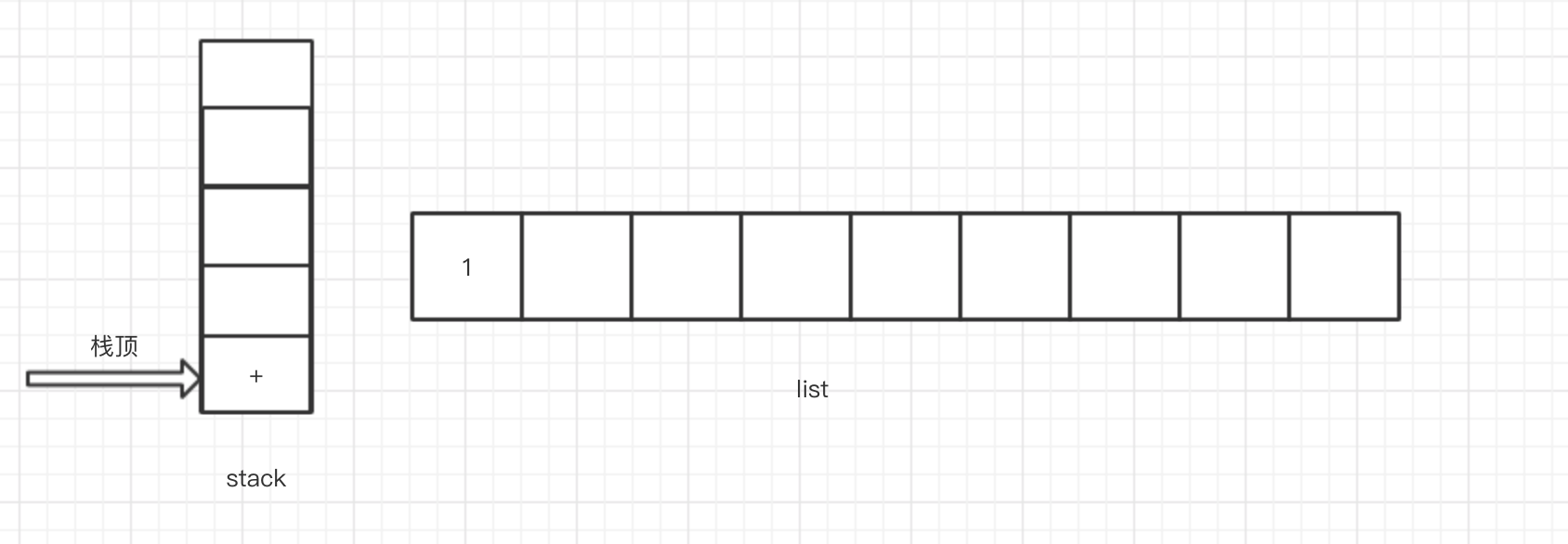
　　4.接下来的两次读取都是左括号，按照我们的规则，左括号直接入栈，此时stack和list结构如下

　　

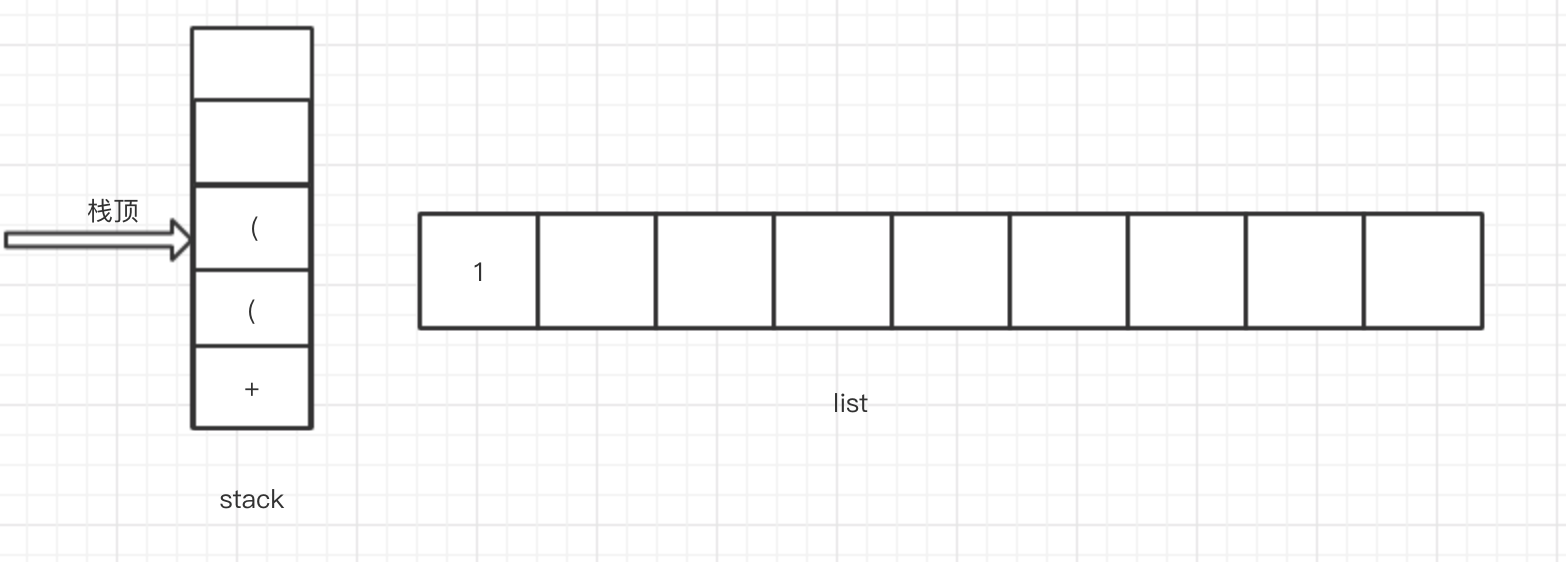
　　5.接着读取到数字2，按照我们的规则，数字直接加入list中，此时stack和list结构如下

　　

　　6.接着读取到操作符+，按照我们的规则，此时栈不为空且栈顶元素为左括号，而只有遇到右括号时，左括号才出栈，所以+运算符直接入栈，此时stack和list结构如下

　　

　　7. 接着读取到数字3，根据我们的规则，数字直接加入list中，此时stack和list结构如下

　　

　　8. 继续向后读取，读到到右括号 ")"，按照我们的规则，执行stack出栈并加入list中操作，直到遇到左括号，并将左括号弹出，但不加入list中，此时stack和list结构如下

　　

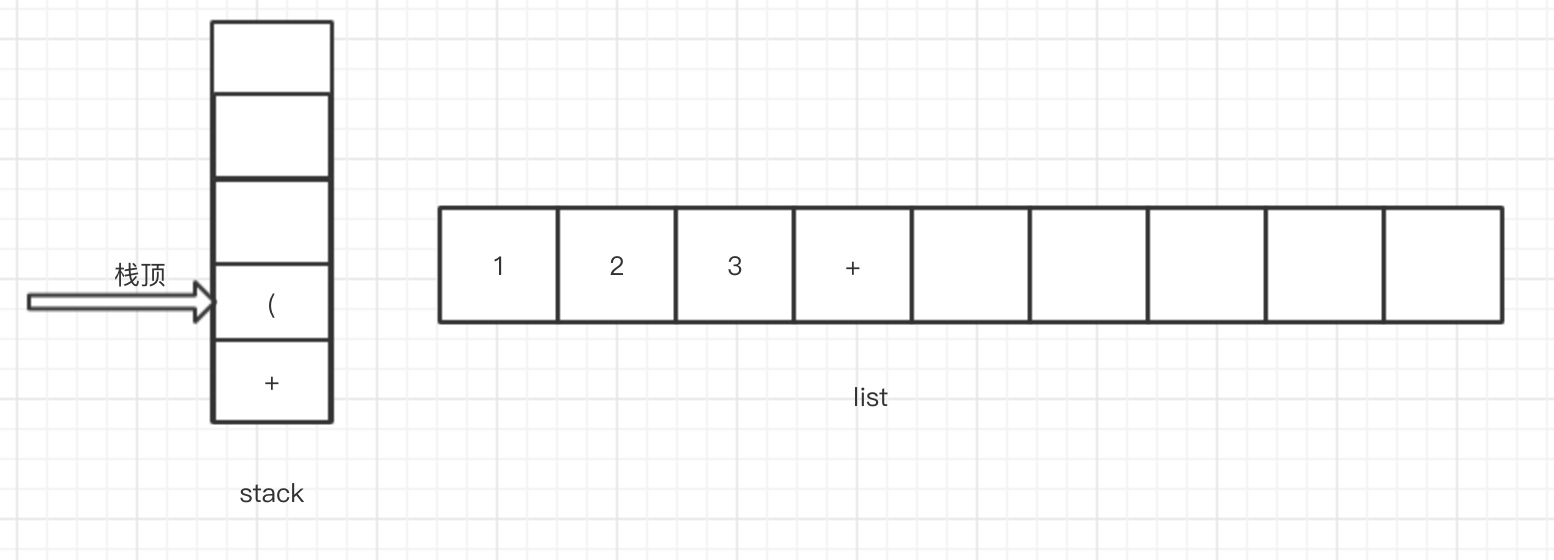
　　9.接着读取到操作符 * ，按照我们的规则，此时栈顶元素为左括号，只需将操作符压栈即可，此时stack和list结构如下

　　

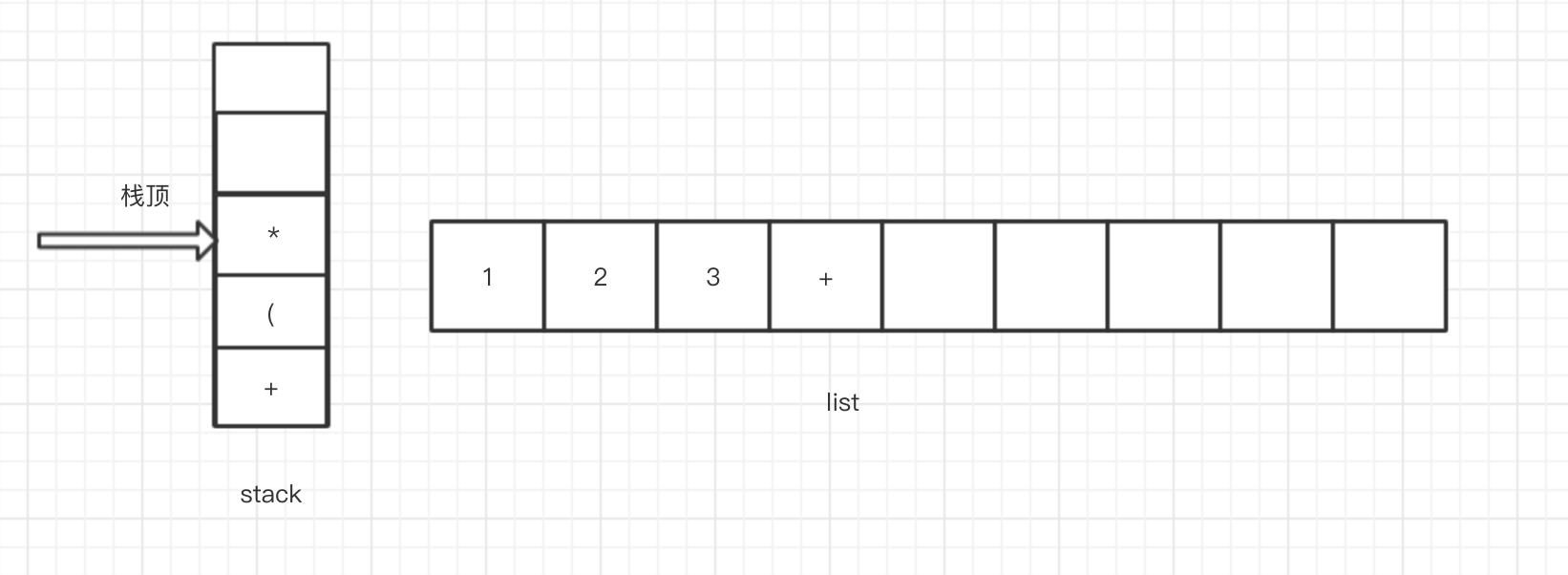
　　10.接下来读取到数字4，按照规则直接将数字加入list中即可，此时stack和list结构如下

　　

　　11.接下来读取到右括号")"，按照我们的规则，执行stack出栈并加入list中操作，直到遇到左括号，并将左括号弹出，但不加入list中，此时stack和list结构如下

　　

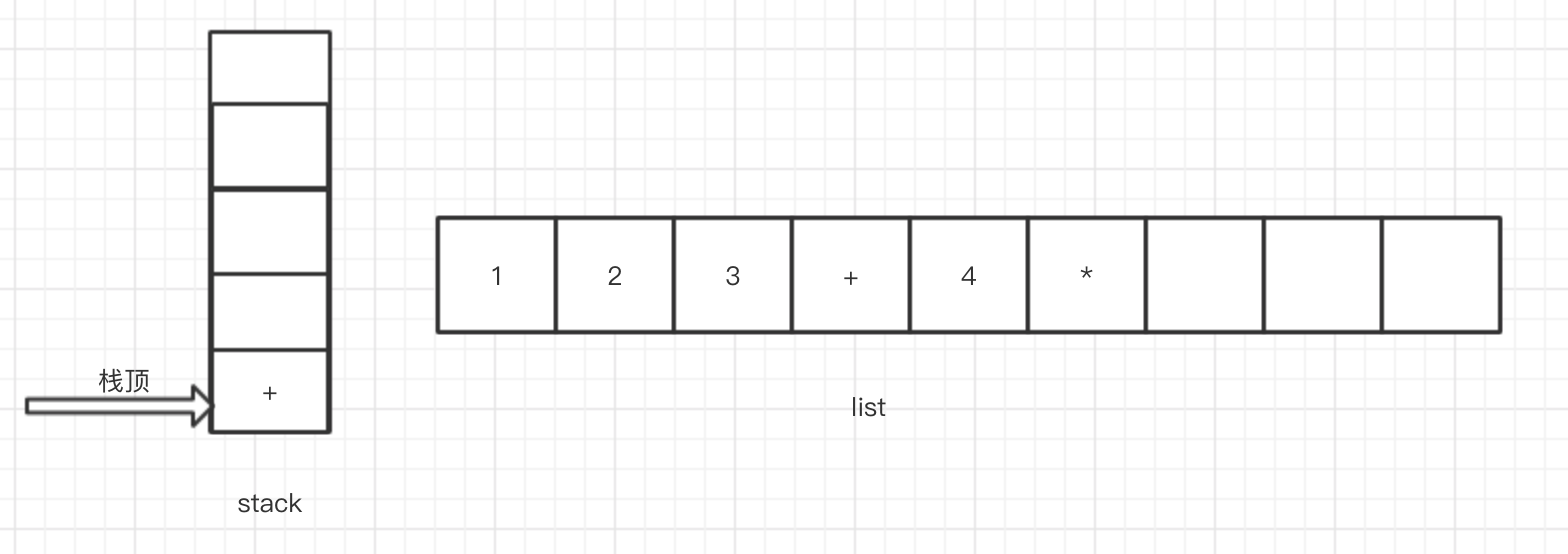
　　12.继续向后读取，此时读取到操作符-，按照我们的规则，当栈不为空且当前优先级小于等于栈顶操作符优先级时，循环执行出栈并加入list操作。循环执行完再将当前操作符入栈

　　

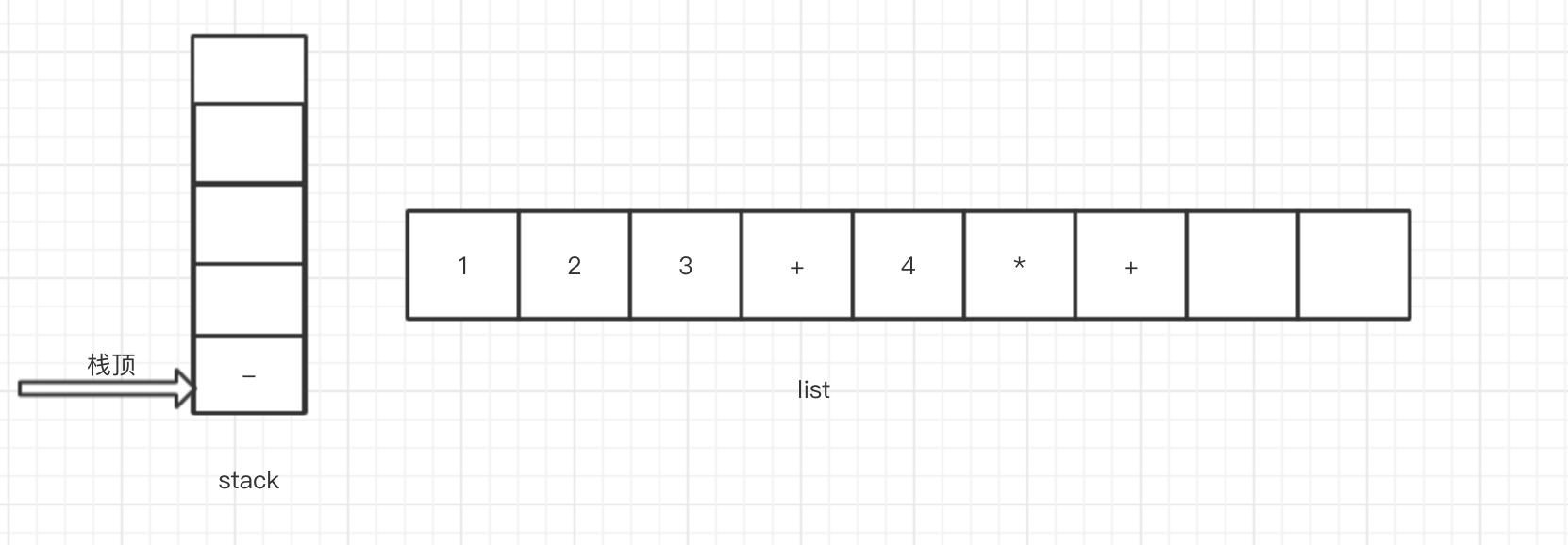
　　13.读取最后一个元素为数字5，按照规则，直接加入list中即可。当表达式读取完后，依此弹出操作符栈中的所有元素，并加入list中，此时stack和list结构如下

　　

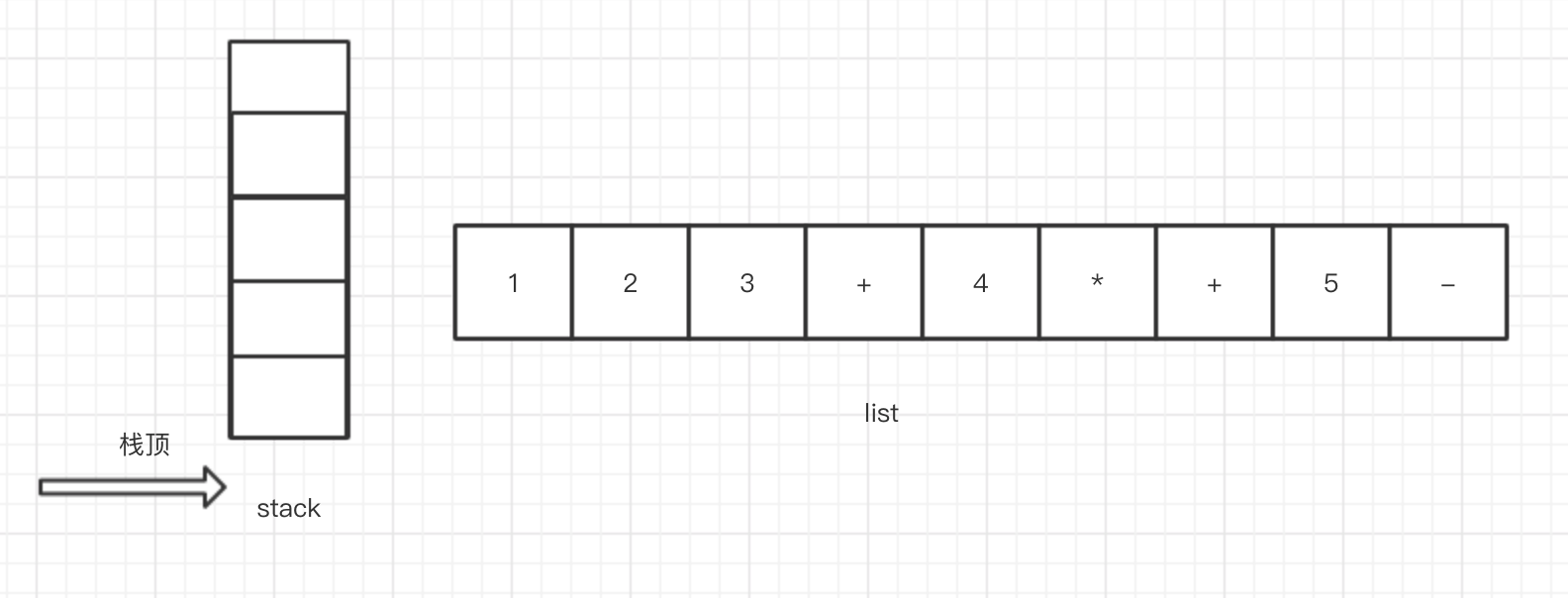
　　此时list中的顺序即为我们转换后的后缀表达式的顺序，即：1 2 3 + 4 * + 5 -

转换代码

 private static List<String> parseToSuffixExpression(List<String> expressionList) {
         //创建一个栈用于保存操作符
         Stack<String> opStack = new Stack<>();
         //创建一个list用于保存后缀表达式
         List<String> suffixList = new ArrayList<>();
         for(String item : expressionList){
             //得到数或操作符
             if(isOperator(item)){
                 //是操作符 判断操作符栈是否为空
                 if(opStack.isEmpty() || "(".equals(opStack.peek()) || priority(item) > priority(opStack.peek())){
                     //为空或者栈顶元素为左括号或者当前操作符大于栈顶操作符直接压栈
                     opStack.push(item);
                 }else {
                     //否则将栈中元素出栈如队，直到遇到大于当前操作符或者遇到左括号时
                     while (!opStack.isEmpty() && !"(".equals(opStack.peek())){
                         if(priority(item) <= priority(opStack.peek())){
                             suffixList.add(opStack.pop());
                         }
                     }
                     //当前操作符压栈
                     opStack.push(item);
                 }
             }else if(isNumber(item)){
                 //是数字则直接入队
                 suffixList.add(item);
             }else if("(".equals(item)){
                 //是左括号，压栈
                 opStack.push(item);
             }else if(")".equals(item)){
                 //是右括号 ，将栈中元素弹出入队，直到遇到左括号，左括号出栈，但不入队
                 while (!opStack.isEmpty()){
                     if("(".equals(opStack.peek())){
                         opStack.pop();
                         break;
                     }else {
                         suffixList.add(opStack.pop());
                     }
                 }
             }else {
                 throw new RuntimeException("有非法字符！");
             }
         }
         //循环完毕，如果操作符栈中元素不为空，将栈中元素出栈入队
         while (!opStack.isEmpty()){
             suffixList.add(opStack.pop());
         }
         return suffixList;
     }
     /**
      * 判断字符串是否为操作符
      * @param op
      * @return
      */
     public static boolean isOperator(String op){
         return op.equals("+") || op.equals("-") || op.equals("*") || op.equals("/");
     }

     /**
      * 判断是否为数字
      * @param num
      * @return
      */
     public static boolean isNumber(String num){
         return num.matches("\\d+");
     }

     /**
      * 获取操作符的优先级
      * @param op
      * @return
      */
     public static int priority(String op){
         if(op.equals("*") || op.equals("/")){
             return 1;
         }else if(op.equals("+") || op.equals("-")){
             return 0;
         }
         return -1;
     }

　　这里为了方便操作，将原中缀表达式字符串转换为list结构，转换list的代码如下

 /**
      * 将表达式转为list
      * @param expression
      * @return
      */
     private static List<String> expressionToList(String expression) {
         int index = 0;
         List<String> list = new ArrayList<>();
         do{
             char ch = expression.charAt(index);
             if(ch < 47 || ch > 58){
                 //是操作符，直接添加至list中
                 index ++ ;
                 list.add(ch+"");
             }else if(ch >= 47 && ch <= 58){
                 //是数字,判断多位数的情况
                 String str = "";
                 while (index < expression.length() && expression.charAt(index) >=47 && expression.charAt(index) <= 58){
                     str += expression.charAt(index);
                     index ++;
                 }
                 list.add(str);
             }
         }while (index < expression.length());
         return list;
     }

　　注：char类型本质为int类型，查看assic码表可知，0～9对应的char在 47~58之间，所以代码依此来判断是数字还是操作符。另外代码中有判断多位数情况，请注意

　　下面展示测试代码

 public static void main(String []args){

         String expression = "1+((2+3)*4)-5";
         List<String> expressionList = expressionToList(expression);
         System.out.println("expressionList="+expressionList);
         //将中缀表达式转换为后缀表达式
         List<String> suffixList = parseToSuffixExpression(expressionList);
         System.out.println(suffixList);
 }

　　测试结果如下：

　　与我们上述描述的结果相同，以上即为中缀表达式转换后缀表达式的过程及相关代码。另外附上根据后缀表达式求值的代码，感兴趣的可以参考

  /**
      * 根据后缀表达式list计算结果
      * @param list
      * @return
      */
     private static int calculate(List<String> list) {
         Stack<Integer> stack = new Stack<>();
         for(int i=0; i<list.size(); i++){
             String item = list.get(i);
             if(item.matches("\\d+")){
                 //是数字
                 stack.push(Integer.parseInt(item));
             }else {
                 //是操作符，取出栈顶两个元素
                 int num2 = stack.pop();
                 int num1 = stack.pop();
                 int res = 0;
                 if(item.equals("+")){
                     res = num1 + num2;
                 }else if(item.equals("-")){
                     res = num1 - num2;
                 }else if(item.equals("*")){
                     res = num1 * num2;
                 }else if(item.equals("/")){
                     res = num1 / num2;
                 }else {
                     throw new RuntimeException("运算符错误！");
                 }
                 stack.push(res);
             }
         }
         return stack.pop();
     }

　　测试运算代码如下

 public static void main(String []args){

         String expression = "1+((2+3)*4)-5";
         List<String> expressionList = expressionToList(expression);
         System.out.println("中缀表达式转为list结构="+expressionList);
         //将中缀表达式转换为后缀表达式
         List<String> suffixList = parseToSuffixExpression(expressionList);
         System.out.println("对应的后缀表达式列表结构="+suffixList);
         //根据后缀表达式计算结果
         int calculateResult = calculate(suffixList);
         System.out.printf(expression+"=%d\n",calculateResult);
 }

　　计算结果如下

总结

　　中缀表达式转后缀表达式的难点在于转换规则，当然这个规则是研究算法的人已经帮我们制定好的，我们只需要按照这个规则实现代码即可。如果上述代码有问题可在留言区回复，谢谢