数据的导入

> data=read.csv('F:/R语言工作空间/pca/data.csv') #数据的导入
>
> ls(data) #ls()函数列出所有变量
[1] "X" "不良贷款率" "存贷款比率" "存款增长率" "贷款增长率" "流动比率" "收入利润率"
[8] "资本充足率" "资本利润率" "资产利润率"
> dim(data) # 维度
[1] 15 10





一.数据标准化




> std_data=scale(data[2:10])  #数据标准化

>

> rownames(std_data)=data[[1]]  #数组各行名字定义为数据文件的的第一列

>

> class(std_data)   #查看数据类型

[1] "matrix"

> df=as.data.frame(std_data)   #转化为数据框

> class(df)

[1] "data.frame"





习惯数据框格式


数据标准化




> std_data=scale(data[2:10])  #数据标准化

>

> rownames(std_data)=data[[1]]  #数组各行名字定义为数据文件的的第一列

>

> class(std_data)   #查看数据类型

[1] "matrix"

> df=as.data.frame(std_data)   #转化为数据框

> class(df)

[1] "data.frame"





　　


二.主成分分析结果




> df.pr=princomp(df,cor=TRUE) #主成分分析

> summary(df.pr,loadings=TRUE)  #列出结果 包含特征向量

Importance of components:

                       Comp.1 Comp.2 Comp.3 Comp.4  Comp.5  Comp.6 Comp.7   Comp.8   Comp.9

Standard deviation     1.8895 1.3087 1.2365 0.9593 0.86553 0.46727 0.4168 0.293547 0.201641

Proportion of Variance 0.3967 0.1903 0.1699 0.1023 0.08324 0.02426 0.0193 0.009574 0.004518

Cumulative Proportion  0.3967 0.5870 0.7569 0.8591 0.94235 0.96661 0.9859 0.995482 1.000000

Loadings:

           Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7 Comp.8 Comp.9

不良贷款率  0.425         0.188  0.288  0.423  0.173  0.695

资本充足率 -0.359        -0.521         0.234  0.546  0.127 -0.214 -0.426

存贷款比率  0.301  0.532 -0.142        -0.370 -0.324  0.248 -0.320 -0.438

流动比率   -0.192  0.429 -0.416  0.439  0.306 -0.384 -0.113         0.399

资产利润率 -0.392  0.332        -0.438 -0.178         0.452  0.494  0.238

资本利润率 -0.413 -0.185  0.259 -0.103  0.428 -0.562  0.167        -0.436

收入利润率 -0.299 -0.455 -0.116  0.299 -0.481 -0.159  0.432 -0.329  0.221

存款增长率 -0.243  0.249  0.387  0.636 -0.282  0.171         0.336 -0.309

贷款增长率 -0.300  0.342  0.518 -0.127  0.101  0.214        -0.620  0.260





　　结果比较杂乱，接下来确定主成分个数


三.确定主因子个数


根据累计贡献率大于90%，确定


计算相关系数矩阵




> cor(df)  #相关系数矩阵

           不良贷款率 资本充足率 存贷款比率 流动比率 资产利润率 资本利润率 收入利润率 存款增长率

不良贷款率     1.0000   -0.57238    0.31761 -0.20055   -0.70121   -0.45662   -0.53825   -0.16790

资本充足率    -0.5724    1.00000   -0.33566  0.61749    0.51053    0.32931    0.37424    0.01208

存贷款比率     0.3176   -0.33566    1.00000  0.16576   -0.02387   -0.72464   -0.56974   -0.11599

流动比率      -0.2005    0.61749    0.16576  1.00000    0.31280    0.07588   -0.03629    0.27787

资产利润率    -0.7012    0.51053   -0.02387  0.31280    1.00000    0.44019    0.13002    0.24387

资本利润率    -0.4566    0.32931   -0.72464  0.07588    0.44019    1.00000    0.38484    0.26496

收入利润率    -0.5383    0.37424   -0.56974 -0.03629    0.13002    0.38484    1.00000    0.24963

存款增长率    -0.1679    0.01208   -0.11599  0.27787    0.24387    0.26496    0.24963    1.00000

贷款增长率    -0.2863    0.03398   -0.14413  0.08791    0.59245    0.55095   -0.09947    0.60455

           贷款增长率

不良贷款率   -0.28628

资本充足率    0.03398

存贷款比率   -0.14413

流动比率      0.08791

资产利润率    0.59245

资本利润率    0.55095

收入利润率   -0.09947

存款增长率    0.60455

贷款增长率    1.00000





　求特征值和特征向量




>y=eigen(cor(df)) #求出cor(df)的特征值和特征向量

> y$values#输出特征值

[1] 3.57008 1.71263 1.52895 0.92033 0.74914 0.21834 0.17370 0.08617 0.04066





　输出前五个累计贡献率　




> sum(y$values[1:5])/sum(y$values)   #求前5个主成分的累计方差贡献率

[1] 0.9423

>





　


输出前5个主成分的载荷矩阵




> df.pr$loadings[,1:5]#输出前5个主成分的载荷矩阵

            Comp.1   Comp.2   Comp.3   Comp.4  Comp.5

不良贷款率  0.4245  0.03196  0.18753  0.28824  0.4226

资本充足率 -0.3595  0.02955 -0.52091  0.04673  0.2341

存贷款比率  0.3013  0.53170 -0.14155 -0.09645 -0.3697

流动比率   -0.1923  0.42903 -0.41595  0.43880  0.3061

资产利润率 -0.3916  0.33239 -0.04543 -0.43786 -0.1780

资本利润率 -0.4134 -0.18527  0.25918 -0.10322  0.4280

收入利润率 -0.2990 -0.45539 -0.11566  0.29949 -0.4810

存款增长率 -0.2432  0.24926  0.38706  0.63621 -0.2824

贷款增长率 -0.3000  0.34207  0.51768 -0.12671  0.1011





　　画出碎石图




screeplot(df.pr,type='lines')  #画出碎石图





　　


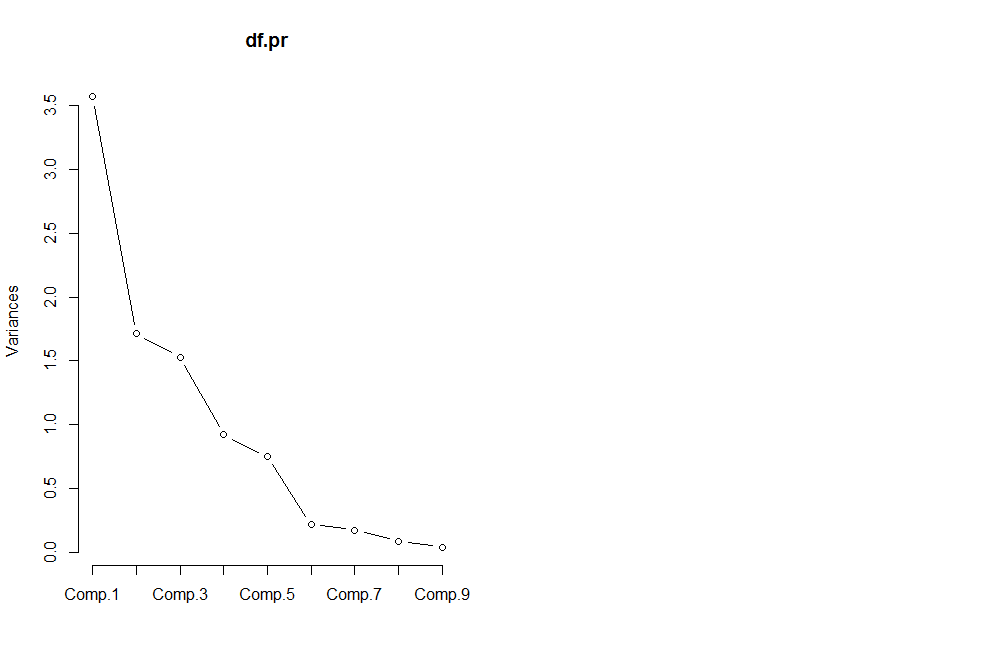
画出散点图


　




biplot(df.pr)     #画出主成分散点图





　　


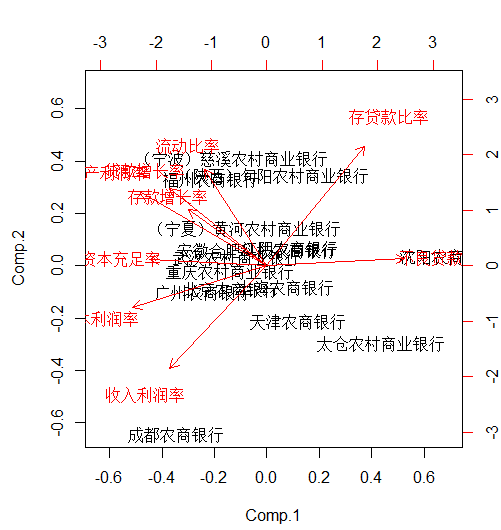
四.获取相关系数矩阵的特征值和特征向量




> y=eigen(cor(df)) #求出cor(df)的特征值和特征向量

> y$values#输出特征值

[1] 3.57008 1.71263 1.52895 0.92033 0.74914 0.21834 0.17370 0.08617 0.04066





　　


五.计算主成分总得分


.




> s=df.pr$scores[,1:5]#输出前5个主成分的得分

> #s[,1]

> #计算综合得分

>

> scores=0.0

> for (i in 1:5)

   scores=(y$values[i]*s[,i])/(sum(y$values[1:5]))+scores

>

>

> cbind(s,scores)#输出综合得分信息

                          Comp.1  Comp.2    Comp.3   Comp.4  Comp.5   scores

北京农商银行             -0.9927 -0.4565 -0.773341  0.72371  0.5357 -0.52362

上海农商银行              0.5461 -0.4069  0.228600 -0.05691 -1.1411  0.08196

广州农商银行             -1.7680 -0.5058  0.091704  0.46582  0.4301 -0.74130

天津农商银行              0.8670 -1.0680 -0.118665 -1.13960 -0.2242 -0.01556

（宁波）慈溪农村商业银行 -0.9713  2.0909 -2.590721  0.44416  0.7692 -0.33751

江阴农商银行              0.6533  0.3486 -1.678249  0.47363 -0.4051  0.05848

成都农商银行             -2.5372 -3.2477  0.008494  0.24227  1.2955 -1.58158

重庆农村商业银行         -1.0099 -0.1061  1.753280  0.23145 -0.6871 -0.16602

（宁夏）黄河农村商业银行 -0.5903  0.7269  1.227349  0.59878 -1.1312  0.08463

（陕西）旬阳农村商业银行  0.1928  1.7666 -0.273642 -1.29087  0.7258  0.31262

太仓农村商业银行          3.1937 -1.4905 -1.089861 -1.17931 -0.6266  0.66358

武汉农村商业银行         -0.8349  0.1686 -0.119553 -1.63283 -0.4856 -0.55902

安徽合肥科技农商银行     -0.2713  0.3084 -0.273867  1.79049 -1.2170 -0.01448

福州农商银行             -1.5557  1.6844  2.185117 -0.80662  0.7243  0.05566

沈阳农商银行              5.0781  0.1871  1.423354  1.13584  1.4374  2.68217





　　


　
												


											
R语言主成分分析（PCA）的更多相关文章
	

    
								
  1. 【转】R语言主成分分析（PCA）
		
    https://www.cnblogs.com/jin-liang/p/9064020.html 数据的导入 > data=read.csv('F:/R语言工作空间/pca/data.csv') ...
    
		
    2. 
						
  2. R语言-主成分分析
		
    1.PCA 使用场景:主成分分析是一种数据降维,可以将大量的相关变量转换成一组很少的不相关的变量,这些无关变量称为主成分 步骤: 数据预处理(保证数据中没有缺失值) 选择因子模型(判断是PCA还是EF ...
    
		
    3. 
						
  3. 主成分分析（PCA）原理及R语言实现
		
    原理: 主成分分析 - stanford 主成分分析法 - 智库 主成分分析(Principal Component Analysis)原理 主成分分析及R语言案例 - 文库 主成分分析法的原理应用及 ...
    
		
    4. 
						
  4. 主成分分析（PCA）原理及R语言实现 | dimension reduction降维
		
    如果你的职业定位是数据分析师/计算生物学家,那么不懂PCA.t-SNE的原理就说不过去了吧.跑通软件没什么了不起的,网上那么多教程,copy一下就会.关键是要懂其数学原理,理解算法的假设,适合解决什么 ...
    
		
    5. 
						
  5. PCA主成分分析   R语言
		
    1. PCA优缺点 利用PCA达到降维目的,避免高维灾难. PCA把所有样本当作一个整体处理,忽略了类别属性,所以其丢掉的某些属性可能正好包含了重要的分类信息 2. PCA原理 条件1:给定一个m*n ...
    
		
    6. 
						
  6. 主成分分析、实例及R语言原理实现
		
    欢迎批评指正! 主成分分析(principal component analysis,PCA) 一.几何的角度理解PCA -- 举例:将原来的三维空间投影到方差最大且线性无关的两个方向(二维空间).  ...
    
		
    7. 
						
  7. R: 主成分分析 ~ PCA(Principal Component Analysis)
		
    本文摘自:http://www.cnblogs.com/longzhongren/p/4300593.html 以表感谢. 综述: 主成分分析 因子分析 典型相关分析,三种方法的共同点主要是用来对数据 ...
    
		
    8. 
						
  8. R语言 PCA
		
    1.关键点 综述:主成分分析 因子分析 典型相关分析,三种方法的共同点主要是用来对数据降维处理的从数据中提取某些公共部分,然后对这些公共部分进行分析和处理. #主成分分析 是将多指标化为少数几个综合指 ...
    
		
    9. 
						
  9. 主成分分析PCA的前世今生
		
    这篇博客会以攻略形式介绍PCA在前世今生. 其实,主成分分析知识一种分析算法,他的前生:应用场景:后世:输出结果的去向,在网上的博客都没有详细的提示.这里,我将从应用场景开始,介绍到得出PCA结果后, ...
    
		
    10. 
		

	


随机推荐
	

    
									
  1. AI的真实感
			
    目录 1.让AI"不完美"--估算和假设 2 AI感知 全能感知 特定感觉无知 3 AI的个性 4 AI的预判 5 AI的智能等级 ​ AI的真实感一直是游戏AI程序员追求的目标, ...
    
			
    2. 
						
  2. hdu 1325 Is It A Tree? (树、node = edge + 1、入度 <= 1、空树)
			
    Is It A Tree?Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)Tota ...
    
			
    3. 
						
  3. nyoj 61-传纸条（一）(双向dp)
			
    61-传纸条(一) 内存限制:64MB 时间限制:2000ms Special Judge: No accepted:8 submit:37 题目描述: 小渊和小轩是好朋友也是同班同学,他们在一起总有 ...
    
			
    4. 
						
  4. opencv 5 图像转换(2 霍夫变换)
			
    霍夫线变换 标准霍夫变换和多尺度霍夫变换(HoughLines()函数) 实例: #include <opencv2/opencv.hpp> #include <opencv2/im ...
    
			
    5. 
						
  5. mysql定时任务(event事件）
			
    1.event事件 事件(event)是MySQL在相应的时刻调用的过程式数据库对象.一个事件可调用一次,也可周期性的启动,它由一个特定的线程来管理的,也就是所谓的“事件调度器” 事件和触发器类似,都 ...
    
			
    6. 
						
  6. [FPGA]Verilog实现JK触发器组成的8421BCD码十进制计数器
			
    目录 概述 电路分析 代码实现 参考文献 概述 本文以异步时序计数器为例,用Verilog实现以\(JK\)触发器组成的8421BCD码十进制异步计数器,并用ModelSim软件进行仿真验证. 电路分 ...
    
			
    7. 
						
  7. 2018092609-2 选题 Scrum立会报告+燃尽图 02
			
    此作业要求参见:[https://edu.cnblogs.com/campus/nenu/2019fall/homework/8683] 一.小组情况组长:迟俊文组员:宋晓丽 梁梦瑶 韩昊 刘信鹏队名 ...
    
			
    8. 
						
  8. (六)OpenStack---M版---双节点搭建---Neutron安装和配置
			
    ↓↓↓↓↓↓↓↓视频已上线B站↓↓↓↓↓↓↓↓ >>>>>>传送门 1.创建网络服务数据库 2.获得 admin 凭证来获取只有管理员能执行的命令的访问权限 3.创 ...
    
			
    9. 
						
  9. vi指令详解
			
    ★ vi的模式(命令模式.插入模式.ex模式) 1)命令模式: 在我们刚刚通过vi新建或打开一个已经存在的文件时,首先默认被读取的模式就是“命令模式”,命令模式的特征就是,在编辑器窗口左下角的位置上没 ...
    
			
    10. 
						
  10. 架构师成长之路5.2-Saltstack远程执行
			
    点击架构师成长之路 架构师成长之路5.2-Saltstack远程执行 配置管理工具: Pupper:1. 采用ruby编程语言:2. 安装环境相对较复杂:3.不支持远程执行,需要FUNC工具配置才可以 ...
    
			
    11.