R-3 t分布--t置信区间--t检验

本节内容：

1：t分布存在的意义是什么

2：t分布的置信区间

3：t分布检验

一、t分布存在的意义是什么

数据分析中有一块很大的版图是属于均值对比的，应用广泛。

例如：对比试验前后病人的症状，证明某种药是否有效；
对比某个班级两次语文成绩，验证是否有提高；
对比某个产品在投放广告前后的销量，看广告是否有效。这些都属于两均值对比的应用。

均值对比的假设检验方法主要有Z检验和T检验：

它们的区别在于Z检验面向总体数据和大样本数据，而T检验适用于小规模抽样样本。

有判断了均值就可以做很多的事情了

二、t分布的置信区间

和计算正态分布的置信区间一样，将正态统计量变成了t分布统计量

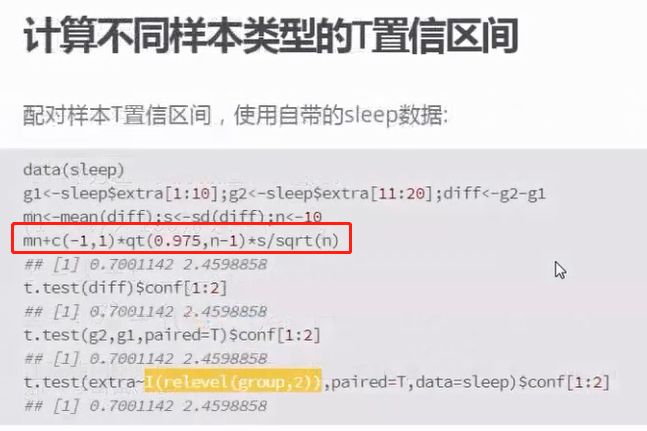
relevel(sleep$group,2)
##将group变成factor类型，2的level最大

得出一下结果：

Paired t-test

data:  extra by relevel(sleep$group, 2)
t = 4.0621, df = 9, p-value = 0.002833
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 0.7001142 2.4598858
sample estimates:
mean of the differences
                   1.58 

三、t分布检验

T检验在使用前有三个应用的注意点：

1、分析的数据对象需要满足正态分布，T检验前需判断样本是否正态分布；
2、分析对比的统计量是均值；
3、对比对象是两个，可以是两个样本；也可以是一个样本和一个常数；

T检验有四种类别：

1、配对样本的T检验--》另类的单样本
独立性检验
    2、等方差的独立样本T检验；
    3、异方差的独立样本T检验；
4、单样本的T检验。 

单样本常用：总体均值跟样本均值的差异
双样本常用：两样本之间的差异
对1跟4的原假设H0 = 总体均值跟样本均值的无差异
对2跟3的原假设H0 = 两样本之间的无差异，即x1=x2

T检验与Z检验不同，需要考虑样本方差是否相同，这是因为自由度决定了T分布曲线，同时，自由度也影响样本方差。

如：匹配样本检验栗子：

所谓配对样本的T检验，是指参与对比的两列数据都是满足正态分布，
而且两列数据之间存在一一对应关系。要想判断这种数据序列之间的差异是否显著，就可以使用配对样本T检验。
处于待检验状态的两列配对样本，应该具有相同的数据个数，而且两列数据在语义上有一一对应关系。
例如对同一个班级的两次考试成绩，这两次成绩都按照学号顺序存放，具有明确的对应关系。

栗子：

采用R自带的sleep为数据集 -> 显示两种催眠药（与对照组相比睡眠时间增加）对10名患者的疗效的数据。

相要知道这个两种药是否有显著性差异？

H0：两种无显著性差异  也集是x1-x2的 d均值为0 -》mu=0 

H1：两种有显著性差异

由于配对样本检验本质是一种单样本T检验，如下：

t.test(sleep$extra[1:10]-sleep$extra[11:20],mu=0)

One Sample t-test

data:  sleep$extra[1:10] - sleep$extra[11:20]
t = -4.0621, df = 9, p-value = 0.002833
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
-2.4598858 -0.7001142
sample estimates:
mean of x
-1.58

结论：p>0.05二者具有显著性差异，拒绝原假设。

如：单样本检验栗子：

全班有52名学生，若学校想知道某个班的英语成绩与全市平均成绩相比是否有差异。

班级μ=79

原假设：平均值=79

备择假设：平均值≠79

H0：79是该市英语平均分，如果结果是接收原假设，那么证明该班的平均分与该市是无差异的。

t.test(data$英语成绩,mu=79)

在该检验结果中，观测到p=2.122*10-11<0.05，拒绝原假设。也就是说，该班的成绩跟全市平均成绩是有显著性差异的。:

如：独立性样本检验

独立样本是两个没有对应关系的独立正态分布数据集合，可以有不同的数据个数，
例如，对同一学校的某次考试，如果需要检验男生与女生的成绩之间有无显著性差异在总体成绩满足正态分布的情况下，
则都可以使用独立样本的T检验，但是在进行T检验之前，需要明确两个样本的方差是否相同，然后根据方差齐性与否选择相应的计算方法。

独立性检验
　　同方差独立T检验
　　　　比如说我们比较城东的房价增长率跟城西的，他们都是来自北京的同个标准差的总体。
　　　　他们之间的差异性只是由于抽样存在的差异
　　异方差独立T检验
　　　　假设样本来自两个不同的总体，就是说是异方差
　　　　他们之间的差异性不止由于抽样存在的差异，还有来自总体的原因。
我们算他们的置信区间，其实是一样的，只不过对于自由度，标准误我们需要取套用各自的公式。

t的独立性样本检验用于检验两样本的均值是否是显著，常用于某二分类变量区间下的连续变量是否有显著性

栗子：

其中。var.equal= T 是两样本的方差一样，关于如何判断是否方差一样我们可以对数据做

方差齐性检验：var.test(avg_exp~gender,data=cre) 得出p为：0.67 不能拒绝原假设

最后得出：

p > 0.05不能拒绝原假设，也就是两样本之间是无显著的。