在VMware下的Linux中的RAID5校验位算法下的磁盘管理

前景：1988年由加利福尼亚大学伯克利分校发表的文章首次提到并定义了RAID，当今CPU性能每年可提升30%-50%但硬盘仅提升7%，渐渐的已经成为计算机整体性能的瓶颈，并且为了避免硬盘的突然损坏导致数据丢失还加入了冗余备份机制。

   RAID5:需要至少三块(含)硬盘，兼顾存储性能、数据安全和储存成本。

RAID5校验位算法下的磁盘管理，  RAID5所要解决的问题是文件的存储与安全问题，一边使存储速度变快，一边使文件安全性跟高。

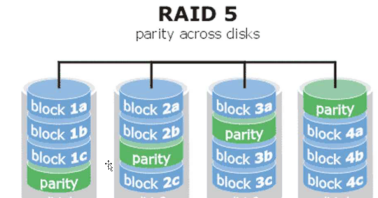
RAID5至少需要三块硬盘，在这里我们使用5块硬盘做演示方便大家理解，有不明白或者不清楚的地方都可以在下面留言

生活中经常可能会出现这样的问题，运维人员需要在硬盘硬件出现故障后手工添加新的磁盘进去，这样会不会比较不方便？
假如初始化RAID5阵列时直接给予5块硬盘，其中2块硬盘设备用于在阵列某块磁盘故障时自动的替换上去，这样很棒吧！开始我们的操作。

开始配置  首先打开到这个界面，点击编辑虚拟机设置（再关掉虚拟机状态下）

点击添加硬盘，添加5个

添加完毕

一样的步骤建4个

之后开启虚拟机

在终端下输入命令：fdisk  -l 查看有没有加入进来  我们发现已经加入进来

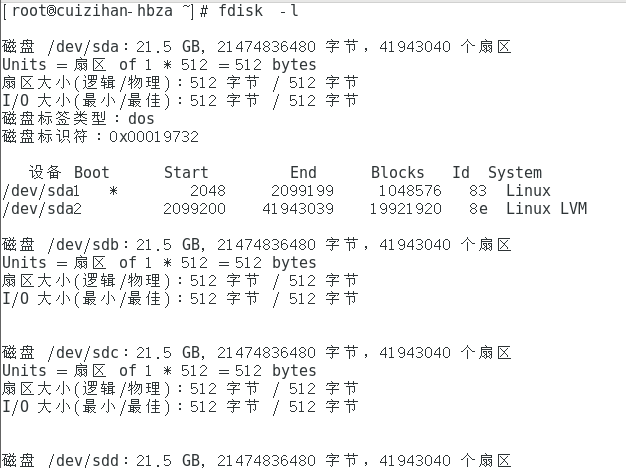
发现加进来了，接下来开始分区转换，创建RAID5并设置2块备份故障盘：

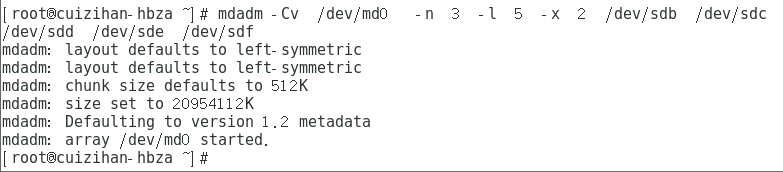
-C代表创建操作，-v显示创建过程，-n是用到的硬盘个数，-l是定义RAID的级别  -x 使备用磁盘格式  而后面写上要加入阵列的硬盘名称， 这里新的磁盘再/dev/md0 下

输入命令：mdadm -Cv  /dev/md0   -n  3  -l  5  -x  2  /dev/sdb  /dev/sdc  /dev/sdd  /dev/sde  /dev/sdf

输入命令： mdadm  -D  /dev/md0  看看有没有按照RAID5进行分区，发现正在分区转换，三个磁盘，两个备份盘（等待转换完成，再开始下一步，已经转换23%）

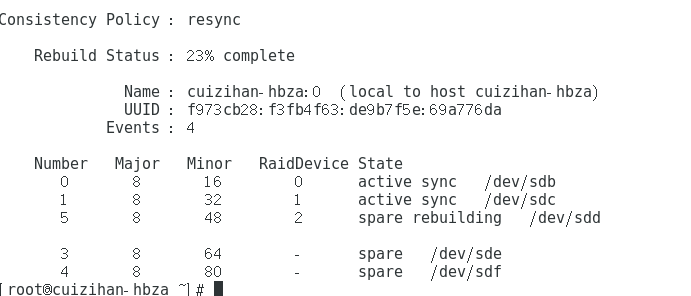
转换完成   （如果前三个盘坏了，备用盘会自动替换掉坏了的硬盘）

输入命令 ：mdadm  -D  /dev/md0   查看我们所建的这个磁盘有多大

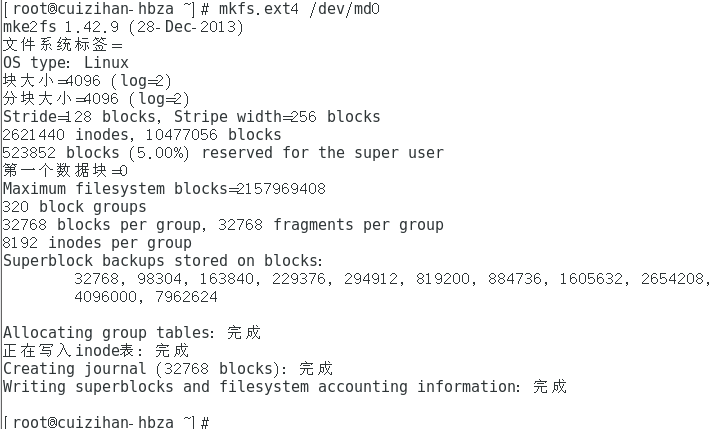
接下来我们将进行格式化，在这里我们格式化成ext4格式，如果不想格式成这个样子，可以输入mkfs之后按两下tab键，会提示你可以用那些格式。

在这里我们格式化成ext4格式，

输入命令： mkfs.ext4 /dev/md0

接下来我们进行挂载

首先创建挂载目录：  mkdir  /media/raid5

进行文件系统的挂载：mount  /dev/md0  /media/raid5

打开桌面发现挂载上了（输入命令：fdisk  -l  也可以看到）

完成

但是这样的挂载只要关机就会消失

关机就没了，可以设置成自动挂载

输入命令：echo  “/dev/md0  /media/raid5  ext4 defaults  0  0”  >>  /etc/fstab

开机还有

接下来我们来实验模仿一个盘被损坏

可以输入命令：mdadm  /dev/md0  -f  /dev/sdb   如果权限不够的话在前面加上一个sudo命令

输入之前（输入命令：mdadm  -D  /dev/md0）

输入之后（此时备用盘正在转换）（可以输入命令：mdadm  -D  /dev/md0来查看）

转换完毕（可以看出sdb是已经坏了的）

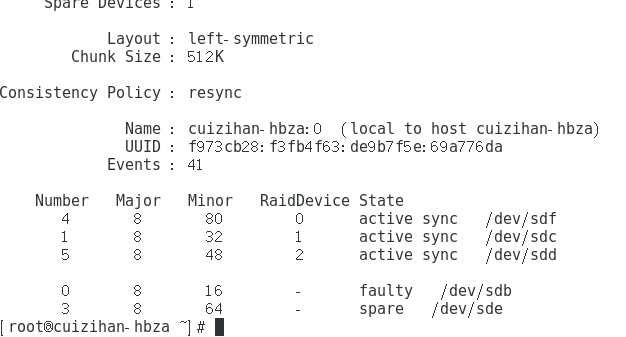
但是此时我们再把/dev/sdb加进去，它会变回来吗？我们来试下

首先重启电脑（不重启的话可能会显示繁忙）

输入命令：mdadm  /dev/md0  -a  /dev/sdb  将磁盘加回去 显示成功

接下来我们看一看它里面的情况，输入命令：mdadm  -D  /dev/md0  并没有显示转换

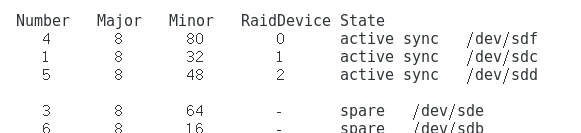
坏了的硬盘即使好了也回不去了

如果有什么问题都可以在下面评论。