logistic回归介绍以及原理分析

1.什么是logistic回归？

logistic回归虽然说是回归，但确是为了解决分类问题，是二分类任务的首选方法，简单来说，输出结果不是0就是1

举个简单的例子：

癌症检测：这种算法输入病理图片并且应该辨别患者是患有癌症（1）或没有癌症（0）

2.logistic回归和线性回归的关系

逻辑回归（Logistic Regression）与线性回归（Linear Regression）都是一种广义线性模型（generalized linear model）。

逻辑回归假设因变量 y 服从二项分布，而线性回归假设因变量 y 服从高斯分布。

因此与线性回归有很多相同之处，去除Sigmoid映射函数的话，逻辑回归算法就是一个线性回归。

可以说，逻辑回归是以线性回归为理论支持的，但是逻辑回归通过Sigmoid函数引入了非线性因素，因此可以轻松处理0/1分类问题。

换种说法：

线性回归，直接可以分为两类，

但是对于图二来说，在角落加上一块蓝色点之后，线性回归的线会向下倾斜，参考紫色的线，

但是logistic回归（参考绿色的线）分类的还是很准确，logistic回归在解决分类问题上还是不错的

3.logistic回归的原理

Sigmoid函数：

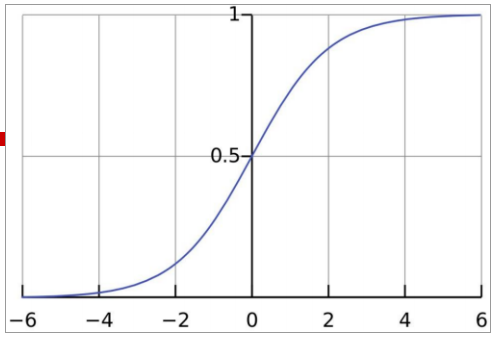
曲线：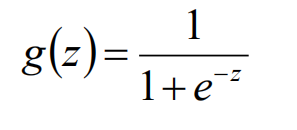

之后推导公式中会用到：

我们希望随机数据点被正确分类的概率最大化，这就是最大似然估计。

最大似然估计是统计模型中估计参数的通用方法。

你可以使用不同的方法（如优化算法）来最大化概率。

牛顿法也是其中一种，可用于查找许多不同函数的最大值（或最小值），包括似然函数。也可以用梯度下降法代替牛顿法。

既然是为了解决二分类问题，其实也就是概率的问题，分类其实都是概率问题，

那咱们先看个概率的问题：

假如有一个罐子，里面有黑白两种颜色的球，数目多少不知，两种颜色的比例也不知。

我们想知道罐中白球和黑球的比例，但我们不能把罐中的球全部拿出来数。

现在我们可以每次任意从已经摇匀的罐中拿一个球出来，记录球的颜色，然后把拿出来的球 再放回罐中。

这个过程可以重复，我们可以用记录的球的颜色来估计罐中黑白球的比例。
假如在前面的一百次重复记录中，
有七十次是白球，请问罐中白球所占的比例最有可能是多少？

解答：

假设白球的概率是p，黑球的概率是1-p

取出100个球，70是白球，30个是黑球，概率：p**70*(1-p)**30

要求出白球所占比例最有可能是多少，其实就是最大似然估计，求导令导函数等于0，求出概率