NOIP201310华容道

题目描述 Description###

小 B 最近迷上了华容道，可是他总是要花很长的时间才能完成一次。于是，他想到用编程来完成华容道：给定一种局面，华容道是否根本就无法完成，如果能完成，最少需要多少时间。

小 B 玩的华容道与经典的华容道游戏略有不同，游戏规则是这样的：在一个 nm 棋盘上有 nm 个格子，其中有且只有一个格子是空白的，其余 nm-1个格子上每个格子上有一个棋子，每个棋子的大小都是 11 的；有些棋子是固定的，有些棋子则是可以移动的；任何与空白的格子相邻（有公共的边）的格子上的棋子都可以移动到空白格子上。游戏的目的是把某个指定位置可以活动的棋子移动到目标位置。给定一个棋盘，游戏可以玩 q 次，当然，每次棋盘上固定的格子是不会变的，但是棋盘上空白的格子的初始位置、指定的可移动的棋子的初始位置和目标位置却可能不同。第 i 次玩的时候，空白的格子在第 EXi 行第 EYi 列，指定的可移动棋子的初始位置为第 SXi 行第 SYi列，目标位置为第 TXi 行第 TYi 列。

假设小 B 每秒钟能进行一次移动棋子的操作，而其他操作的时间都可以忽略不计。请你告诉小 B 每一次游戏所需要的最少时间，或者告诉他不可能完成游戏。

输入描述 Input Description###

第一行有 3 个整数，每两个整数之间用一个空格隔开，依次表示 n、m 和 q；

接下来的 n 行描述一个 n*m 的棋盘，每行有 m 个整数，每两个整数之间用一个空格隔开，每个整数描述棋盘上一个格子的状态，0 表示该格子上的棋子是固定的，1 表示该格子上的棋子可以移动或者该格子是空白的。接下来的 q 行，每行包含 6 个整数依次是 EXi、EYi、SXi、SYi、TXi、TYi，每两个整数之间用一个空格隔开，表示每次游戏空白格子的位置，指定棋子的初始位置和目标位置。

输出描述 Output Description###

输出有 q 行，每行包含 1 个整数，表示每次游戏所需要的最少时间，如果某次游戏无法完成目标则输出−1。

样例输入 Sample Input###

3 4 2 0 1 1 1 0 1 1 0 0 1 0 0 3 2 1 2 2 2 1 2 2 2 3 2

样例输出 Sample Output###

2

-1

数据范围及提示 Data Size & Hint###

【输入输出样例说明】

棋盘上划叉的格子是固定的，红色格子是目标位置，圆圈表示棋子，其中绿色圆圈表示目标棋子。

第一次游戏，空白格子的初始位置是 (3, 2)（图中空白所示），游戏的目标是将初始位置在(1, 2)上的棋子（图中绿色圆圈所代表的棋子）移动到目标位置(2, 2)（图中红色的格子）上。

移动过程如下：

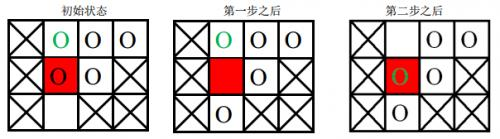
第二次游戏，空白格子的初始位置是（1, 2）（图中空白所示），游戏的目标是将初始位置在（2, 2）上的棋子（图中绿色圆圈所示）移动到目标位置 (3, 2)上。

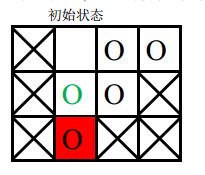
要将指定块移入目标位置，必须先将空白块移入目标位置，空白块要移动到目标位置，必然是从位置（2， 2）上与当前图中目标位置上的棋子交换位置，之后能与空白块交换位置的只有当前图中目标位置上的那个棋子，因此目标棋子永远无法走到它的目标位置，游戏无法完成。

【数据范围】

对于 30%的数据，1 ≤ n, m ≤ 10，q = 1；

对于 60%的数据，1 ≤ n, m ≤ 30，q ≤ 10；

对于 100%的数据，1 ≤ n, m ≤ 30，q ≤ 500。

之前的一些废话###

深夜了。

题解###

看到题思考了1分钟决定上无脑大BFS，其中$dis(i,j,k,l)$表示空白格子在$(i,j)$目标格子在$(k,l)$的最少步数。于是说干就干了。30分钟后70分到手，得分效率是不是贼高!

至于正解的话。

代码###

#include<iostream>

#include<algorithm>

#include<cstring>

#include<cmath>

#include<cstdio>

#include<queue>

#include<cstdlib>

using namespace std;

typedef long long LL;

#define mem(a,b) memset(a,b,sizeof(a))

typedef pair<int,int> PII;

typedef pair<PII,PII> PPP;

#define X first

#define Y second

#define MP make_pair

inline int read()

{

	int x=0,f=1;char c=getchar();

	while(!isdigit(c)){if(c=='-')f=-1;c=getchar();}

	while(isdigit(c)){x=x*10+c-'0';c=getchar();}

	return x*f;

}

const int maxn=35;

int n,m,pic[maxn][maxn],q,dis[maxn][maxn][maxn][maxn],dx[4]={1,0,-1,0},dy[4]={0,1,0,-1};

bool vis[maxn][maxn][maxn][maxn];

PII empty,s,t;

queue <PPP> Q;

bool illegal(int X,int Y){return X<0 || X>=n || Y<0 || Y>=m || !pic[X][Y];}

void solve()

{

	mem(dis,42);mem(vis,0);

	while(Q.size())Q.pop();

	int ans=100000;

	empty.X=read()-1;empty.Y=read()-1;

	s.X=read()-1;s.Y=read()-1;

	t.X=read()-1;t.Y=read()-1;

	dis[empty.X][empty.Y][s.X][s.Y]=0;

	vis[empty.X][empty.Y][s.X][s.Y]=1;

	Q.push(MP(MP(empty.X,empty.Y),MP(s.X,s.Y)));

	if(s.X==t.X && s.Y==t.Y){printf("0\n");return;}

	while(Q.size())

	{

		PPP now=Q.front();Q.pop();

		for(int i=0;i<4;i++)

		{

			int nx=now.X.X+dx[i],ny=now.X.Y+dy[i];

			if(illegal(nx,ny))continue;

			if(nx==now.Y.X && ny==now.Y.Y)

			{

				if(vis[nx][ny][now.X.X][now.X.Y])continue;

				dis[nx][ny][now.X.X][now.X.Y]=dis[now.X.X][now.X.Y][now.Y.X][now.Y.Y]+1;

				vis[nx][ny][now.X.X][now.X.Y]=1;

				Q.push(MP(MP(nx,ny),MP(now.X.X,now.X.Y)));

				if(t.X==now.X.X && t.Y==now.X.Y)ans=min(ans,dis[nx][ny][now.X.X][now.X.Y]);

			}

			else

			{

				if(vis[nx][ny][now.Y.X][now.Y.Y])continue;

				dis[nx][ny][now.Y.X][now.Y.Y]=dis[now.X.X][now.X.Y][now.Y.X][now.Y.Y]+1;

				vis[nx][ny][now.Y.X][now.Y.Y]=1;

				Q.push(MP(MP(nx,ny),MP(now.Y.X,now.Y.Y)));

				if(t.X==now.Y.X && t.Y==now.Y.Y)ans=min(ans,dis[nx][ny][now.Y.X][now.Y.Y]);

			}

		}

	}

	printf("%d\n", ans!=100000 ? ans : -1);

	return;

}

int main()

{

    n=read();m=read();q=read();

    for(int i=0;i<n;i++)for(int j=0;j<m;j++)pic[i][j]=read();

    while(q--)solve();

	return 0;

}

总结###

极其热爱这种暴力好写并且得分得的又多的题