可用性库存(CO09)排除库存地点增强
1、业务需求
1.1、业务背景
1.2、对应方案:
2、测试BAPI
首先运行事务代码CO09,查看结果
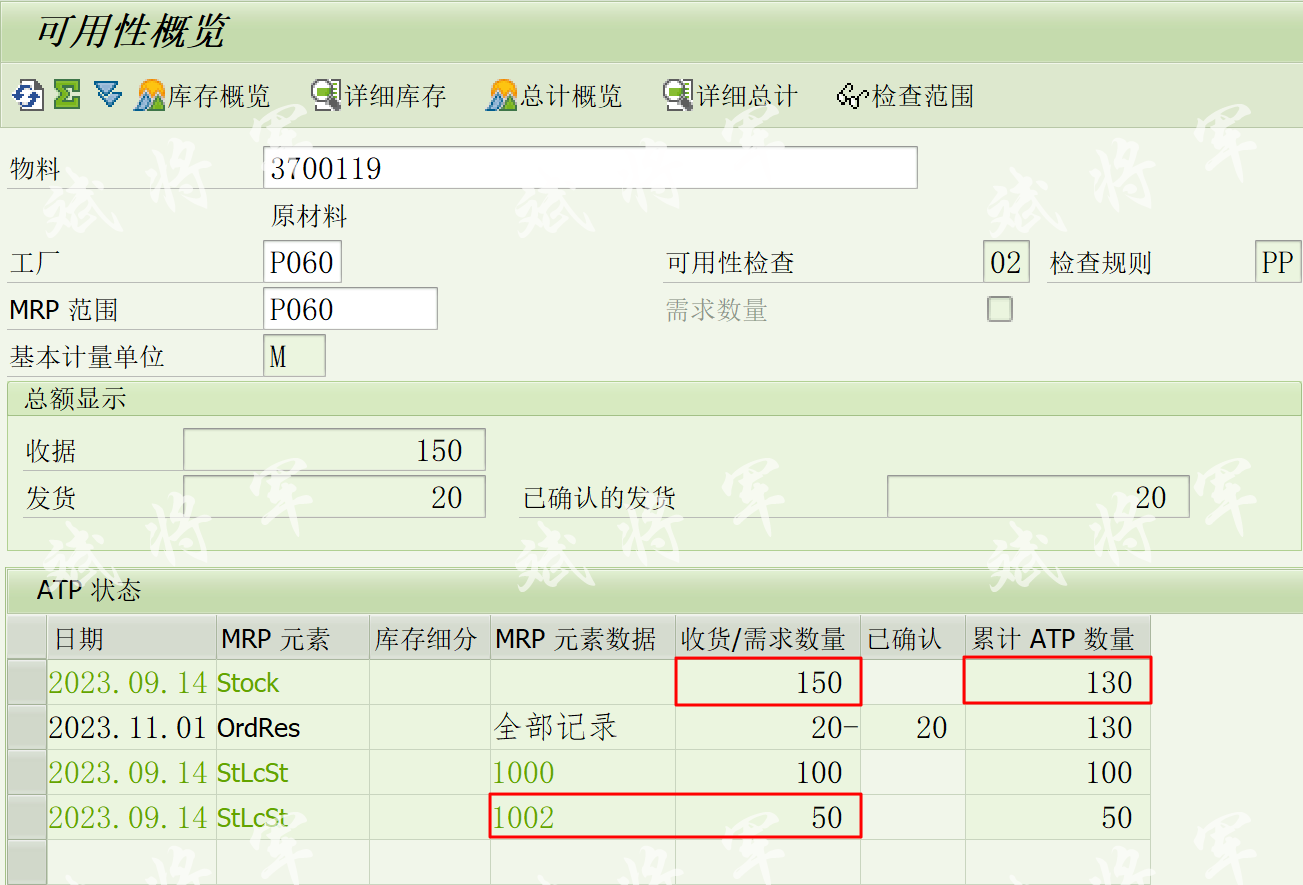
运行BAPI_MATERIAL_AVAILABILITY
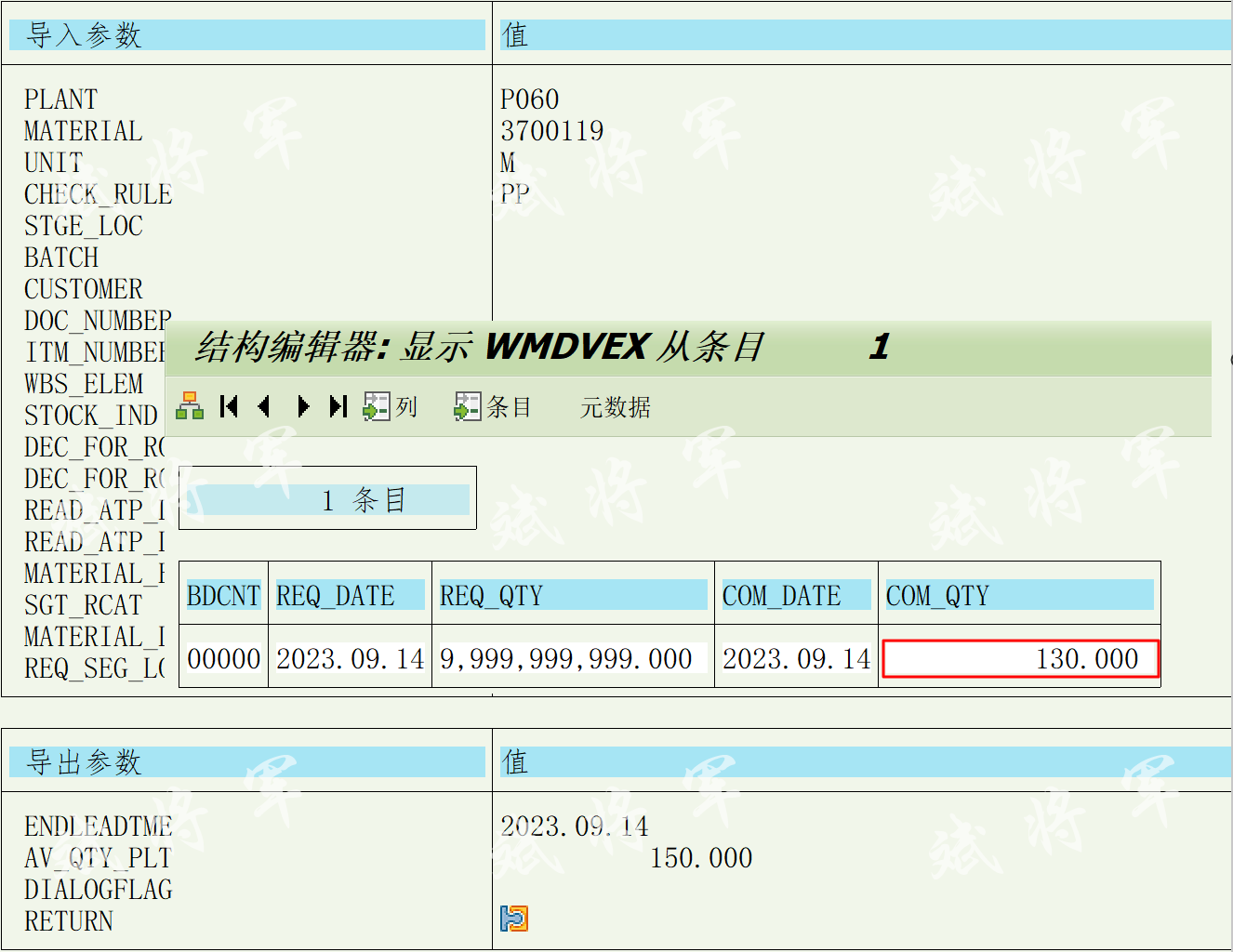
3、增强实现
3.1、增强思路
3.2、EXIT_SAPLATPC_001(未采用)
3.3、STOCK_RECEIPT_ISSUE_READ
4、调试过程
博客频遭盗窃,请移步公众号“斌将军”,输入关键字“可用性库存”查看

可用性库存(CO09)排除库存地点增强的更多相关文章
- SAP MM 销售订单库存与普通库存之间相互转换过账后对于EBEWH以及MBEWH表的更新
SAP MM 销售订单库存与普通库存之间相互转换过账后对于EBEWH以及MBEWH表的更新 1,DEMO数据 物料号:1300009995 工厂:2160 销售订单号/item号:0010097627 ...
- SAP MM 特殊库存之T库存初探
SAP MM 特殊库存之T库存初探 笔者所在的A项目里,销售业务广泛启用了POD功能.VL02N对交货单做了发货过账后物权并没有转移,而是将自有E库存转为一个叫做在途库存的特殊库存里.等到货物到了客户 ...
- 【MM系列】SAP MM 非限制/可用库存
公众号:SAP Technical 本文作者:matinal 原文出处:http://www.cnblogs.com/SAPmatinal/ 原文链接:[MM系列]SAP MM 非限制/可用库存 ...
- MM52 历史库存及历史金额查询
"表:TABLES:MSEG,LFA1,MARA,EKPO,EKKO,MARD,EKBE,EKET.********************************************* ...
- Odoo 的库存管理与OpenERP之前的版本有了很大的不同,解读Odoo新的WMS模块中的新特性
原文来自:http://shine-it.net/index.php/topic,16409.0.html 库存移动(Stock Move)新玩法Odoo的库存移动不仅仅是存货在两个“存货地点”之间的 ...
- Odoo 库存管理-库存移动(Stock Move)新玩法
库存移动(Stock Move)新玩法 Odoo的库存移动不仅仅是存货在两个“存货地点”之间的移动的基本概念了,他们可以被“串联”在一起,可以用来生成或改变其对应的拣货单 (Picking).链式库存 ...
- EBS业务学习之库存管理
库存管理业务流程 企业结构 库存结构 库存结构定义 指定每个子库存的特性: •子库存的数量跟踪 •资产类子库存 •保留子库存 •净值子库存 •包含在有效承诺中Include in ATP •子库存级库 ...
- SAP库存历史库存表更新逻辑 (转)
根据库存类型的不同,库存信息保存在不同的表中,具体而言见下表 库存类型 当前库存 历史库存 库存金额 历史库存金额 工厂级别库存 MARC MARCH MBEW MBEWH MBEW 库存地点库存 M ...
- 「SAP技术」为正常库存管理的物料做成本中心采购会是什么结果?
SAP 为正常库存管理的物料做成本中心采购会是什么结果? 这种采购可以正常进行,收货后SAP会更新采购订单里指定的费用类科目,而库存数量和库存价值都不会增加. 1, 如下物料号,是正常做库存管理的物料 ...
- APS系统帮助寻找企业最优库存
零库存模式的实施要有深厚的民族文化和企业文化为支点.随着对零库存管理研究的深入,就会发现它不仅仅是一种运营管理技术,更是一种文化.一种哲学. 当这种认同文化体现在企业与企业之间时,就会表现出彼此的认同 ...
随机推荐
- 高效开发与设计:提效Spring应用的运行效率和生产力
引言 现状和背景 Spring框架是广泛使用的Java开发框架之一,它提供了强大的功能和灵活性,但在大型应用中,由于Spring框架的复杂性和依赖关系,应用的启动时间和性能可能会受到影响.这可能导致开 ...
- python之猜数字小游戏
import random#随机数函数 a = random.randint(0, 50)#随机0-50之内的整数 print('------------------SWS工作室----------- ...
- 记录一个异常 Gradle打包项目Lombok不生效 No serializer found for class com.qbb.User and no properties discovered to create BeanSerializer......
完整的错误: 03-Dec-2022 16:57:22.941 涓ラ噸 [http-nio-8080-exec-5] org.apache.catalina.core.StandardWrapperV ...
- c语言指针数组和数组指针
1 #include<stdio.h> 2 #include<iostream> 3 using namespace std; 4 int main(){ 5 int a[2] ...
- MySQL 8.0.32 InnoDB ReplicaSet 配置和手动切换
1.环境准备 主库:192.168.137.4 mytest3 从库:192.168.137.5 mytest4 MySQL: 8.0.32 2.配置 ReplicaSet 实例 启动 mysql s ...
- ElasticSearch之cat transforms API
命令样例如下: curl -X GET "https://localhost:9200/_cat/transforms?v=true&format=json" --cace ...
- dotnet-dump工具使用
介绍 dotnet-dump 是 .NET Core 官方工具之一,用于生成和分析 .NET Core 进程的转储文件(dump file).它可以帮助开发人员在应用程序发生故障或性能问题时进行故障排 ...
- Linux的期末冲刺
选择 一.Linux基础 Linux目录结构 相关命令: cd, ls, pwd 详解: Linux 目录结构采用树状结构,根目录为 /.用户的帐户信息保存在 /etc/passwd 文件中,包括用户 ...
- OPPO关停自研芯片公司哲库,这对行业将产生什么影响?
OPPO什么时候关停自研芯片公司哲库? 公元2023年5月12日,OPPO关停了自研芯片公司哲库.这也是汶川大地震的日子,而OPPO创始人是四川人,真是冥冥之中自有天意.OPPO公司在一份声明中表示, ...
- 13、Flutter AspectRatio 调整子元素child的宽高比
AspectRatio的作用是根据设置调整子元素child的宽高比. childAspectRatio 是 GridView 和 AspectRatio 控件中的一个参数 AspectRati ...
