2021-02-22：一个象棋的棋盘，然后把整个棋盘放入第一象限，棋盘的最左下角是(0,0)位置，那么整个棋盘就是横坐标上9条线、纵坐标上10条线的区域。给你三个 参数 x，y，k。返回“马”从(0,0)位置出发，必须走k步。最后落在(x,y)上的方法数有多少种?

2021-02-22：一个象棋的棋盘，然后把整个棋盘放入第一象限，棋盘的最左下角是(0,0)位置，那么整个棋盘就是横坐标上9条线、纵坐标上10条线的区域。给你三个 参数 x，y，k。返回“马”从(0,0)位置出发，必须走k步。最后落在(x,y)上的方法数有多少种?

福哥答案2021-02-22：

自然智慧即可。

1.递归。有代码。

2.记忆化搜索。有代码。

3.动态规划。dp是三维数组。棋盘是二维数组，走k步，需要k+1个棋盘。有代码。

4.动态规划，空间压缩。只有相邻棋盘才有依赖，所以只需要用两个棋盘，就能走完。有代码。

代码用golang编写，代码如下：

package main

import "fmt"

func main() {

    a := 3
    b := 4
    k := 5
    fmt.Println("1.递归：", jump1(a, b, k))
    fmt.Println("---")
    fmt.Println("2.记忆化搜索：", jump2(a, b, k))
    fmt.Println("---")
    fmt.Println("3.动态规划：", jump3(a, b, k))
    fmt.Println("---")
    fmt.Println("4.动态规划,空间压缩：", jump4(a, b, k))
}

func jump1(a int, b int, k int) int {
    return process1(0, 0, k, a, b)
}
func process1(x int, y int, rest int, a int, b int) int {
    if x < 0 || x >= 9 || y < 0 || y >= 10 {
        return 0
    }
    if rest == 0 {
        if x == a && y == b {
            return 1
        } else {
            return 0
        }
    }
    ways := process1(x+2, y+1, rest-1, a, b)
    ways += process1(x+2, y-1, rest-1, a, b)
    ways += process1(x-2, y+1, rest-1, a, b)
    ways += process1(x-2, y-1, rest-1, a, b)
    ways += process1(x+1, y+2, rest-1, a, b)
    ways += process1(x+1, y-2, rest-1, a, b)
    ways += process1(x-1, y+2, rest-1, a, b)
    ways += process1(x-1, y-2, rest-1, a, b)
    return ways
}

func jump2(a int, b int, k int) int {
    dp := make([][][]int, 10)
    for i := 0; i < 10; i++ {
        dp[i] = make([][]int, 9)
        for j := 0; j < 9; j++ {
            dp[i][j] = make([]int, k+1)
            for m := 0; m < k+1; m++ {
                dp[i][j][m] = -1
            }
        }
    }
    return process2(0, 0, k, a, b, dp)
}
func process2(x int, y int, rest int, a int, b int, dp [][][]int) int {
    if x < 0 || x >= 10 {
        return 0
    }
    if y < 0 || y >= 9 {
        return 0
    }
    if dp[x][y][rest] != -1 {
        return dp[x][y][rest]
    }
    if rest == 0 {
        if x == a && y == b {
            dp[x][y][rest] = 1
            return 1
        } else {
            dp[x][y][rest] = 0
            return 0
        }
    }
    ways := process2(x+2, y+1, rest-1, a, b, dp)
    ways += process2(x+2, y-1, rest-1, a, b, dp)
    ways += process2(x-2, y+1, rest-1, a, b, dp)
    ways += process2(x-2, y-1, rest-1, a, b, dp)
    ways += process2(x+1, y+2, rest-1, a, b, dp)
    ways += process2(x+1, y-2, rest-1, a, b, dp)
    ways += process2(x-1, y+2, rest-1, a, b, dp)
    ways += process2(x-1, y-2, rest-1, a, b, dp)
    dp[x][y][rest] = ways
    return ways

}

func jump3(a int, b int, k int) int {
    dp := make([][][]int, 10)
    for i := 0; i < 10; i++ {
        dp[i] = make([][]int, 9)
        for j := 0; j < 9; j++ {
            dp[i][j] = make([]int, k+1)
        }
    }
    dp[a][b][0] = 1
    for rest := 1; rest <= k; rest++ {
        for x := 0; x < 10; x++ {
            for y := 0; y < 9; y++ {
                ways := pick3(x+2, y+1, rest-1, dp)
                ways += pick3(x+1, y+2, rest-1, dp)
                ways += pick3(x-1, y+2, rest-1, dp)
                ways += pick3(x-2, y+1, rest-1, dp)
                ways += pick3(x-2, y-1, rest-1, dp)
                ways += pick3(x-1, y-2, rest-1, dp)
                ways += pick3(x+1, y-2, rest-1, dp)
                ways += pick3(x+2, y-1, rest-1, dp)
                dp[x][y][rest] = ways
            }
        }
    }
    return dp[0][0][k]
}
func pick3(x int, y int, rest int, dp [][][]int) int {
    if x < 0 || x >= 10 || y < 0 || y >= 9 {
        return 0
    }
    return dp[x][y][rest]
}

func jump4(a int, b int, k int) int {
    dp := make([][][]int, 10)
    for i := 0; i < 10; i++ {
        dp[i] = make([][]int, 9)
        for j := 0; j < 9; j++ {
            dp[i][j] = make([]int, 2)
        }
    }
    dp[a][b][0] = 1
    for rest := 1; rest <= k; rest++ {
        for x := 0; x < 10; x++ {
            for y := 0; y < 9; y++ {
                ways := pick4(x+2, y+1, dp)
                ways += pick4(x+1, y+2, dp)
                ways += pick4(x-1, y+2, dp)
                ways += pick4(x-2, y+1, dp)
                ways += pick4(x-2, y-1, dp)
                ways += pick4(x-1, y-2, dp)
                ways += pick4(x+1, y-2, dp)
                ways += pick4(x+2, y-1, dp)
                dp[x][y][1] = ways
            }
        }
        for i := 0; i < 10; i++ {
            for j := 0; j < 9; j++ {
                dp[i][j][0], dp[i][j][1] = dp[i][j][1], 0
            }
        }
    }
    return dp[0][0][0]
}
func pick4(x int, y int, dp [][][]int) int {
    if x < 0 || x >= 10 || y < 0 || y >= 9 {
        return 0
    }
    return dp[x][y][0]
}

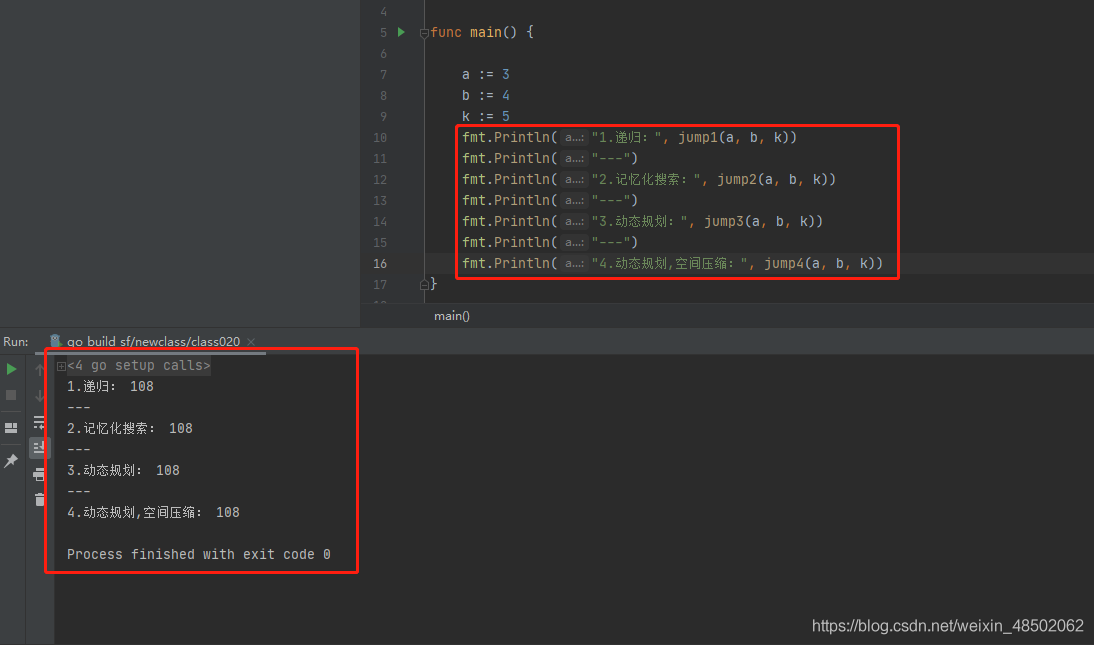
执行结果如下：

---

左神java代码

评论