回溯理论基础及leetcode例题

学习参考

回溯

与递归相辅相成;回溯是递归的副产品，只要有递归就会有回溯。

回溯函数也就是递归函数，指的都是一个函数。

回溯搜索法

纯暴力搜索

解决的问题

组合问题：N个数里面按一定规则找出k个数的集合

切割问题：一个字符串按一定规则有几种切割方式

子集问题：一个N个数的集合里有多少符合条件的子集

排列问题：N个数按一定规则全排列，有几种排列方式(与组合差别，排列有元素顺序)

棋盘问题：N皇后，解数独等等

理解

抽象的不易理解；抽象为图形结构--树形结构

N叉树【树的宽度：集合的大小（for处理）；深度：递归的深度（递归处理）】

模板

void backtracking(参数){
  if(终止条件){
    收集结果；
    return；
  }

  //单层搜索
   for(选择：本层集合中元素（树中节点孩子的数量就是集合的大小)）{//集合元素集
      处理节点；
      backtracking(路径，选择列表);//递归函数；
      回溯操作； //（12，把2回溯，变13；没有回溯操作就会递归为123）
    }
  return；
}

递归里面嵌套for循环，for循环里又有递归

leetcode题目

组合

77.组合

for循环嵌套太多层了

树形结构



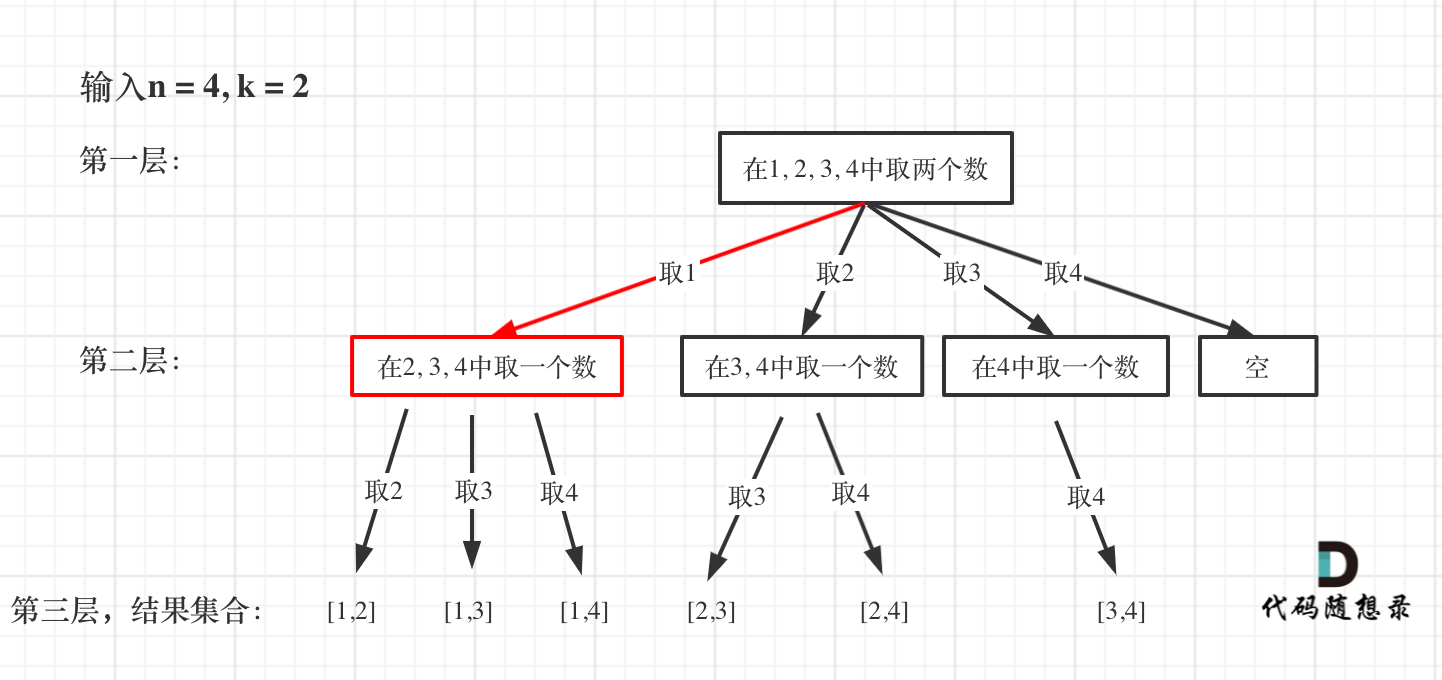
不能取前面的的：因为组合是无序的，会重复；

每个节点都是一个for循环

回溯三部曲

递归函数参数返回值

确定终止条件

单层递归逻辑

伪代码

全局变量：二维数组res【返回值】
         一维数组path【单个结果】
//确定返回值参数
void backtracking(n,k,start){//n集合大小；k需要的子集合大小；start每个取值的开始；
  //确定终止条件
  if(path.size == k){
    res.add(path);
    return;
  }
  //单层递归逻辑
  //对于1，234节点
  for(i=start,i<=n;i++){
    path.push(i);//1
    backtracking(n,k,i+1);//遍历剩下的集合234；
    path.pop();//回溯过程
  }
}

实现

java版本

class Solution {
    List<List<Integer>> res = new ArrayList<List<Integer>>();
    List<Integer> path = new ArrayList<Integer>();

    public List<List<Integer>> combine(int n, int k) {
        backtracking(n,k,1);
        return res;
    }

    public void backtracking(int n,int k,int start){
        if(path.size() == k){
            res.add(new ArrayList<>(path));//容易犯错误
            return;
        }

        for(int i=start;i<=n;i++){//i<=n -(k-path.size()) + 1 会减少运行时间【剪枝操作】
            path.add(i);
            backtracking(n,k,i+1);
            path.remove(path.size()-1);
        }

    }
}

问题：参考

在链表path里面添加值，然后把path链表添加进res链表中，在做算法题的时候，平时使用res.add(path)，结果发现输出打印为空：

在链表path里面添加值，然后把path链表添加进res链表中，在做算法题的时候，平时使用res.add(path)，结果发现输出打印为空：	res.add(new ArrayList＜＞(path))和res.add(path)的区别
共同点：	都是向res这个ArrayList中填加了一个名为path的链表
不同点：	res.add(new ArrayList(path))：开辟一个独立地址，地址中存放的内容为path链表，后续path的变化不会影响到res
	res.add(path)：将res尾部指向了path地址，后续path内容的变化会导致res的变化。

优化：剪枝

可以剪枝的地方就在递归中每一层的for循环所选择的起始位置。

如果for循环选择的起始位置之后的元素个数 已经不足 我们需要的元素个数了，那么就没有必要搜索了。

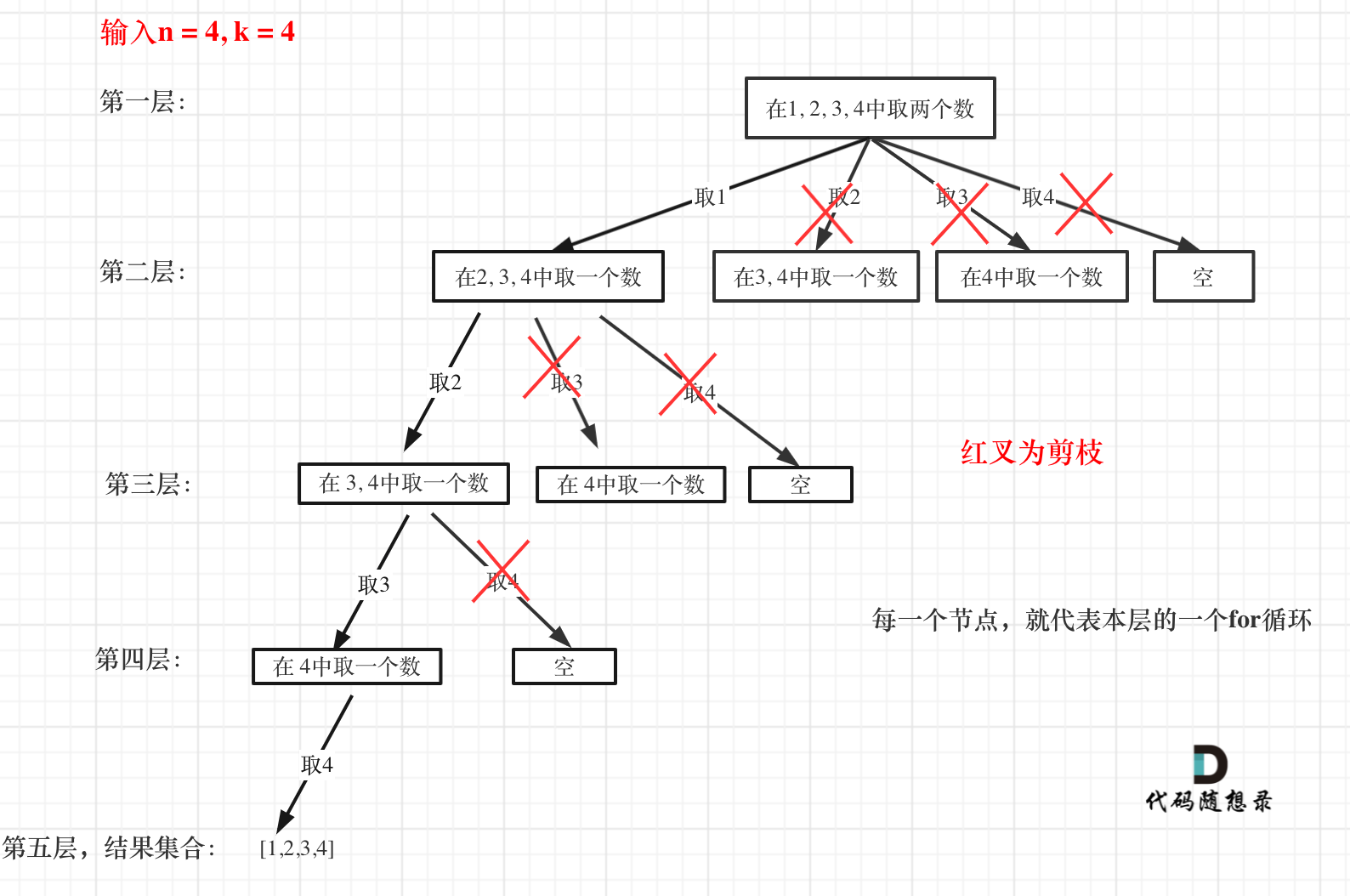
优化过程如下：

已经选择的元素个数：path.size();

所需需要的元素个数为: k - path.size();

列表中剩余元素（n-i） >= 所需需要的元素个数（k - path.size()）

在集合n中至多要从该起始位置 : i <= n - (k - path.size()) + 1，开始遍历

分割

131. 分割回文串

树形结构

回溯三部曲

递归函数参数返回值

确定终止条件

单层递归逻辑

伪代码

收集结果路径

void backtracking(string s,startIndex){
    //终止条件
    //即切割线是终止条件
    if(startIndex >= s.length()){
        res.add(path);
        return;
    }

    //单层递归逻辑
    //切割字串范围：(startIndex,i]
    for(i=startIndex;i< s.length();i++){
      if(isPalindrome(s,startIndex,i)){
          path.add(子串)；
      }else continue；

      backtracking(s,i+1);
      path.remove(path.size()-1);
    }
}

实现

java版本

class Solution {
    List<List<String>> result = new ArrayList<List<String>>();
    List<String> path = new ArrayList<String>();

    public List<List<String>> partition(String s) {
        backtracking(s,0);
        return result;
    }

    public void backtracking(String s,int startIndex){
        if(startIndex >= s.length()){
            result.add(new ArrayList<String>(path));
            return;
        }

        for(int i=startIndex;i<s.length();i++){
            String sub = s.substring(startIndex,i+1);
            if(isPalindrome(sub)){
                path.add(sub);
            }else {continue;}

            backtracking(s,i+1);
            path.remove(path.size()-1);
        }
    }

    public boolean isPalindrome(String s){
        int left = 0;
        int right = s.length()-1;

        while(left<right){
            if(s.charAt(left) != s.charAt(right)){
                return false;
            }
            left++;
            right--;
        }
        return true;
    }
}

子集问题

78. 子集

树形结构



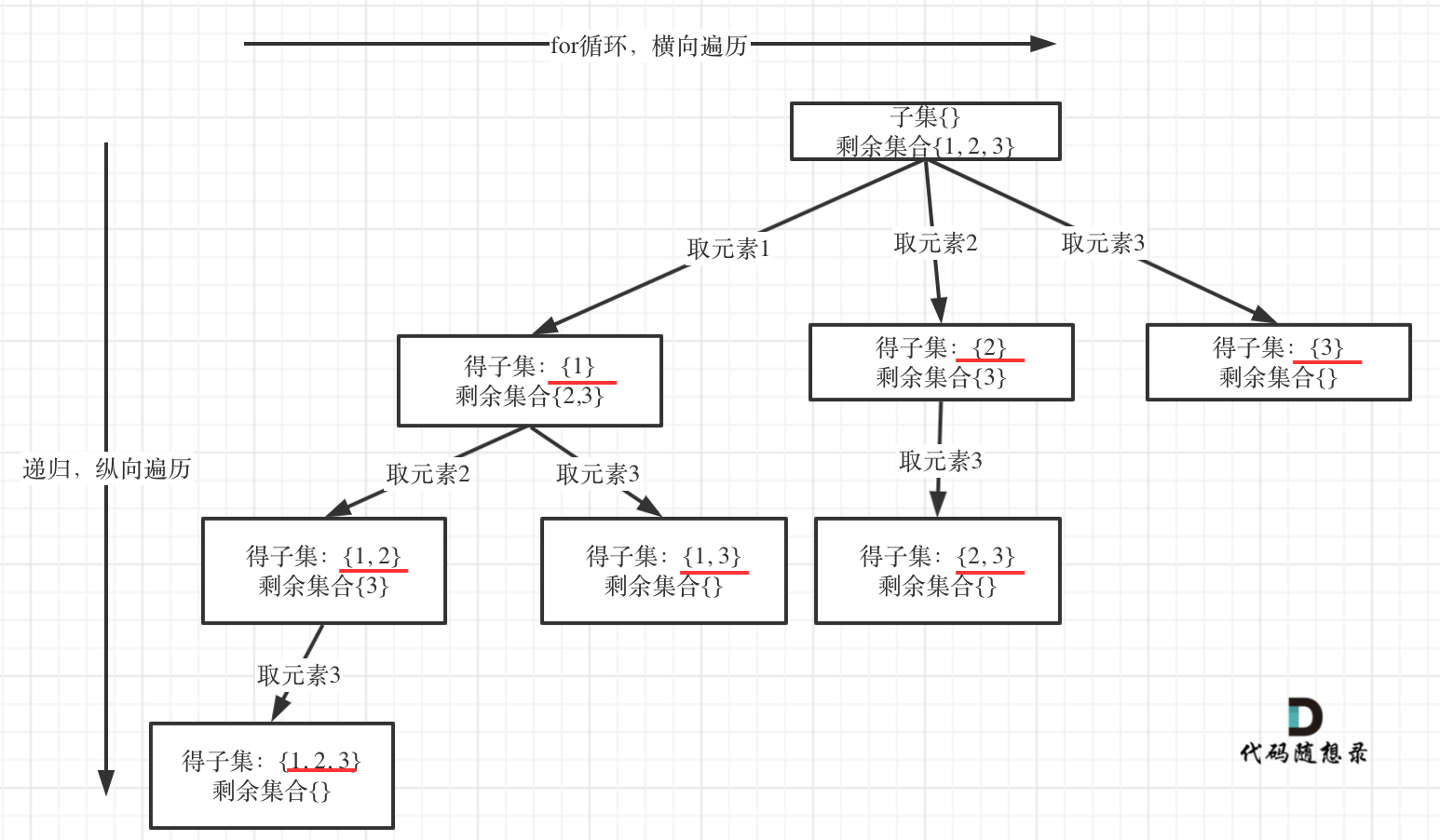
收获结果的时候：在每个节点收获结果

组合和分割问题都是在叶子节点里取结果；

伪代码

void backtracking(nums,stratIndex){
  result.add(path);

  if(stratIndex >= path.size()) return;

  for(int i=startIndex;i<nums.length;i++){
    path.add(nums[i]);
    backtracking(nums,i+1);
    path.remove(path.size()-1);
  }
}

实现

class Solution {
    List<List<Integer>> list = new ArrayList<List<Integer>>();
    List<Integer> path= new ArrayList<Integer>();
    public List<List<Integer>> subsets(int[] nums) {
        backtracking(nums,0);
        return list;
    }

    public void backtracking(int[] nums,int stratIndex){
        list.add(new ArrayList<Integer>(path));
        if(stratIndex>=nums.length){
            return;
        }

        for(int i=stratIndex;i<nums.length;i++){
            path.add(nums[i]);
            backtracking(nums,i+1);
            path.remove(path.size()-1);
        }
    }
}

排列

46.全排列

树形结构

伪代码：

void backtracking(nums,used){
  if(path.size() == nums.length){
    res.add(path);
    return;
  }

  for(i=0;i<nums.length;i++){
    if(used[i] == true) continue;
    used[i] = true;
    path.add(nums[i]);
    backtracking(nums,used);
    used[i] = false;
    path.remove(path.size()-1);
  }
}

实现

class Solution {
    List<List<Integer>> list = new ArrayList<List<Integer>>();
    List<Integer> path = new ArrayList<Integer>();

    public List<List<Integer>> permute(int[] nums) {
        boolean[] used = new boolean[nums.length];
        backtracking(nums,used);
        return list;
    }

    public void backtracking(int[] nums,boolean[] used){
        if(path.size() >= nums.length){
            list.add(new ArrayList<>(path));
            return;
        }

        for(int i=0;i<nums.length;i++){
            if(used[i] == true) continue;

            path.add(nums[i]);
            used[i] = true;
            backtracking(nums,used);
            path.remove(path.size()-1);
            used[i] = false;
        }
    }
}