P5047 [Ynoi2019 模拟赛] Yuno loves sqrt technology II 题解

题目链接：Yuno loves sqrt technology II

很早以前觉得还挺难的一题。本质就是莫队二次离线，可以参考我这篇文章的讲述莫队二次离线 P5501 [LnOI2019] 来者不拒，去者不追 题解。

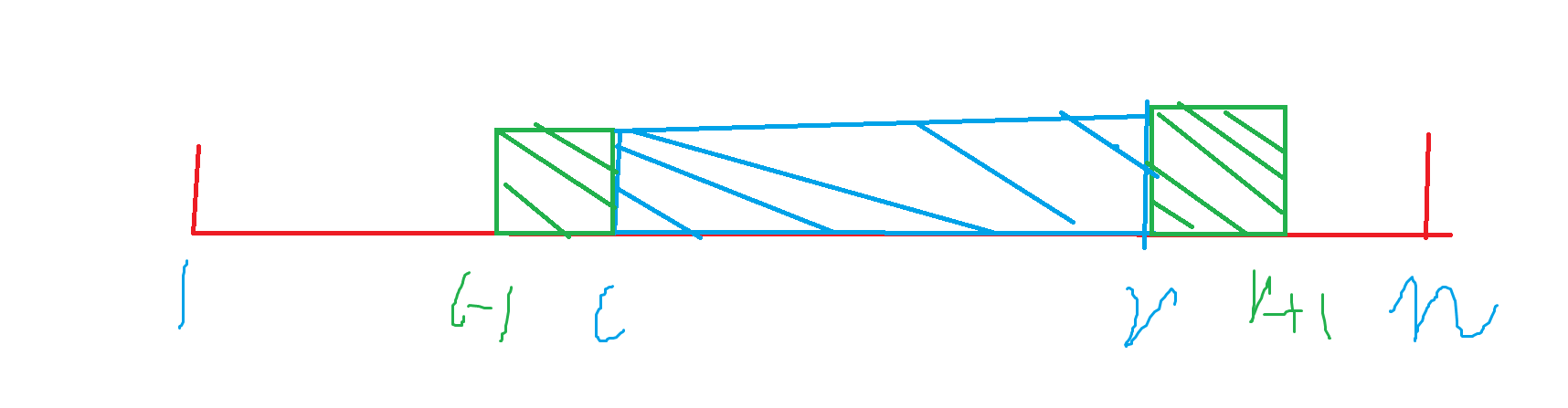
注意到左右两边莫队的端点移动，贡献效果是不一样的：

1. \(r \rightarrow r+1\)，会增加 \([l,r]\) 上比它大的数。

2. \(l \rightarrow l-1\)，会增加 \([l,r]\) 上比它小的数。

所以我们拆分成 \([1,r]\) 上比 \(a_{当前} \ 大/小\) 的数的数量去减去 \([1,l-1]\) 上比 \(a_{当前} \ 大/小\) 的数的数量。然后很显然，就是经典的莫二套路了，一个用扫描线 \(+\) 值域分块来算，一个预处理来算。

所以我们需要维护一波树状数组预处理出每个点对前缀区间的逆序对贡献情况，然后判断的时候，左端点的移动是看比它小的值数量，而右端点的移动则是更大值数量。至于如何查找，首先我们先查找出 \(\ge x\) 的数量，然后直接用当前区间的数量减去它得到比它小的数量，而大于的数量，只需要减去重复相等的数量即可，开个桶维护就行，记得离散化，剩余见代码注释即可。

参照代码

#include <bits/stdc++.h>

//#pragma GCC optimize("Ofast,unroll-loops")

#define isPbdsFile

#ifdef isPbdsFile

#include <bits/extc++.h>

#else

#include <ext/pb_ds/priority_queue.hpp>
#include <ext/pb_ds/hash_policy.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <ext/pb_ds/trie_policy.hpp>
#include <ext/pb_ds/tag_and_trait.hpp>
#include <ext/pb_ds/hash_policy.hpp>
#include <ext/pb_ds/list_update_policy.hpp>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/exception.hpp>
#include <ext/rope>

#endif

using namespace std;
using namespace __gnu_cxx;
using namespace __gnu_pbds;
typedef long long ll;
typedef long double ld;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
typedef tuple<int, int, int> tii;
typedef tuple<ll, ll, ll> tll;
typedef unsigned int ui;
typedef unsigned long long ull;
typedef __int128 i128;
#define hash1 unordered_map
#define hash2 gp_hash_table
#define hash3 cc_hash_table
#define stdHeap std::priority_queue
#define pbdsHeap __gnu_pbds::priority_queue
#define sortArr(a, n) sort(a+1,a+n+1)
#define all(v) v.begin(),v.end()
#define yes cout<<"YES"
#define no cout<<"NO"
#define Spider ios_base::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);
#define MyFile freopen("..\\input.txt", "r", stdin),freopen("..\\output.txt", "w", stdout);
#define forn(i, a, b) for(int i = a; i <= b; i++)
#define forv(i, a, b) for(int i=a;i>=b;i--)
#define ls(x) (x<<1)
#define rs(x) (x<<1|1)
#define endl '\n'
//用于Miller-Rabin
[[maybe_unused]] static int Prime_Number[13] = {0, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37};

template <typename T>
int disc(T* a, int n)
{
    return unique(a + 1, a + n + 1) - (a + 1);
}

template <typename T>
T lowBit(T x)
{
    return x & -x;
}

template <typename T>
T Rand(T l, T r)
{
    static mt19937 Rand(time(nullptr));
    uniform_int_distribution<T> dis(l, r);
    return dis(Rand);
}

template <typename T1, typename T2>
T1 modt(T1 a, T2 b)
{
    return (a % b + b) % b;
}

template <typename T1, typename T2, typename T3>
T1 qPow(T1 a, T2 b, T3 c)
{
    a %= c;
    T1 ans = 1;
    for (; b; b >>= 1, (a *= a) %= c)if (b & 1)(ans *= a) %= c;
    return modt(ans, c);
}

template <typename T>
void read(T& x)
{
    x = 0;
    T sign = 1;
    char ch = getchar();
    while (!isdigit(ch))
    {
        if (ch == '-')sign = -1;
        ch = getchar();
    }
    while (isdigit(ch))
    {
        x = (x << 3) + (x << 1) + (ch ^ 48);
        ch = getchar();
    }
    x *= sign;
}

template <typename T, typename... U>
void read(T& x, U&... y)
{
    read(x);
    read(y...);
}

template <typename T>
void write(T x)
{
    if (typeid(x) == typeid(char))return;
    if (x < 0)x = -x, putchar('-');
    if (x > 9)write(x / 10);
    putchar(x % 10 ^ 48);
}

template <typename C, typename T, typename... U>
void write(C c, T x, U... y)
{
    write(x), putchar(c);
    write(c, y...);
}

template <typename T11, typename T22, typename T33>
struct T3
{
    T11 one;
    T22 tow;
    T33 three;

    bool operator<(const T3 other) const
    {
        if (one == other.one)
        {
            if (tow == other.tow)return three < other.three;
            return tow < other.tow;
        }
        return one < other.one;
    }

    T3() { one = tow = three = 0; }

    T3(T11 one, T22 tow, T33 three) : one(one), tow(tow), three(three)
    {
    }
};

template <typename T1, typename T2>
void uMax(T1& x, T2 y)
{
    if (x < y)x = y;
}

template <typename T1, typename T2>
void uMin(T1& x, T2 y)
{
    if (x > y)x = y;
}

constexpr int N = 1e5 + 10;
int a[N], b[N];
hash2<int, int> mp; //离散化
int pos[N]; //序列分块
int n, m;

struct Mo
{
    int l, r, id;

    bool operator<(const Mo& other) const
    {
        return pos[l] ^ pos[other.l] ? l < other.l : pos[l] & 1 ? r < other.r : r > other.r;
    }
} node[N];

constexpr int MX = 1e5;
int repeat[MX];
int bit[N];
//查找>=x 的树状数组
inline void add(int x)
{
    while (x)bit[x]++, x -= lowBit(x);
}

inline int query(int x)
{
    int ans = 0;
    while (x <= MX)ans += bit[x], x += lowBit(x);
    return ans;
}

//预处理前缀区间的大于与小于当前位置的数的数量
int preBig[N], preSmall[N];
ll ans[N]; //答案
vector<tuple<int, int, int, bool>> seg[N]; //扫描线[l,r,id,isBig]
constexpr int ValSize = sqrt(MX); //值域分块的大小
constexpr int CNT = (MX + ValSize - 1) / ValSize; //值域分块的数量
int preVal[N], prePosVal[N]; //值域分块的块前缀和块内单点前缀和
int valPos[N], s[N], e[N]; //值域分块每个点的块编号,块的起点和终点

inline void addVal(const int val)
{
    const int pos = valPos[val]; //当前值域块编号
    //更新前缀和
    forn(i, pos, CNT)preVal[i]++;
    forn(i, val, e[pos])prePosVal[i]++;
}

//拿到(>val的数量,<val的数量)
inline pii queryCnt(const int val)
{
    const int pos = valPos[val];
    //注意块内第一个点前面的点的编号不是0,是上一个块的右端点
    int bigEqual = preVal[CNT] - preVal[pos - 1] - (val - 1 >= s[pos] ? prePosVal[val - 1] : 0); //大于等于的数量
    int big = bigEqual - repeat[val]; //去掉等于的数量
    int small = preVal[CNT] - bigEqual;
    return pii(big, small);
}

inline void solve()
{
    read(n, m);
    const int siz = sqrt(n);
    forn(i, 1, n)read(a[i]), b[i] = a[i], pos[i] = (i - 1) / siz + 1;
    //离散化
    sortArr(b, n);
    const int c = disc(b, n);
    forn(i, 1, c)mp[b[i]] = i;
    forn(i, 1, n)a[i] = mp[a[i]];
    //预处理单点前缀贡献
    forn(i, 1, n)
    {
        int bigEqual = query(a[i]); //拿到>=a[i] 的数量
        preSmall[i] = i - 1 - bigEqual; //前面区间共i-1个数,不包括当前这个数
        preBig[i] = bigEqual - repeat[a[i]]; //去相等的就是大于的数了
        add(a[i]);
        repeat[a[i]]++;
    }
    memset(repeat, 0, sizeof repeat); //后面要用重置
    forn(i, 1, m)
    {
        auto& [l,r,id] = node[i];
        read(l, r);
        id = i;
    }
    sortArr(node, m);
    int l = 1, r = 0;
    //记得判断是大于的贡献还是小于的贡献
    forn(i, 1, m)
    {
        auto [L,R,id] = node[i];
        auto& Ans = ans[id];
        if (l > L)seg[r].emplace_back(L, l - 1, id, false);
        while (l > L)Ans -= preSmall[--l];
        if (l < L)seg[r].emplace_back(l, L - 1, -id, false);
        while (l < L)Ans += preSmall[l++];
        if (r < R)seg[l - 1].emplace_back(r + 1, R, -id, true);
        while (r < R)Ans += preBig[++r];
        if (r > R)seg[l - 1].emplace_back(R + 1, r, id, true);
        while (r > R)Ans -= preBig[r--];
    }
    //值域分块预处理
    forn(i, 1, MX)valPos[i] = (i - 1) / ValSize + 1;
    forn(i, 1, CNT)s[i] = (i - 1) * ValSize + 1, e[i] = i * ValSize;
    e[CNT] = MX;
    //扫描线
    forn(i, 1, n)
    {
        addVal(a[i]);
        repeat[a[i]]++;
        for (auto [l,r,id,isBig] : seg[i])
        {
            int add_del = id / abs(id); //加还是减
            id = abs(id);
            forn(j, l, r)
            {
                auto [big,small] = queryCnt(a[j]); //拿到两种贡献
                ans[id] += add_del * (isBig ? big : small); //对应的计算贡献
            }
        }
    }
    forn(i, 1, m)ans[node[i].id] += ans[node[i - 1].id]; //注意每个是对前面答案的差分,需要前缀和复原
    forn(i, 1, m)write(endl, ans[i]);
}

signed int main()
{
    // MyFile
    Spider
    //------------------------------------------------------
    int test = 1;
    //    read(test);
    // cin >> test;
    forn(i, 1, test)solve();
    //    while (cin >> n, n)solve();
    //    while (cin >> test)solve();
}

\[最终时间复杂度为\ O(n\log{V_{max}}+2 \times m\sqrt{n}+n\sqrt{V_{max}})
\]