学习笔记：勒让德（Legendre）符号

授课老师：ybx、chh。

授课时间：2024/3/8。

授课内容纲要：勒让德符号及其性质（欧拉准则，高斯引理，二次互反律）。

勒让德符号概括

好像在 OI 和 MO 当中都挺有用的。

勒让德符号的定义

假设 \(p\) 为奇质数，\(a\in U_p\)（\(U_p=\{1,2,\dots,p-1\}\)），则：

\[\left(\dfrac ap\right)=\begin{cases}1&\text{exist } x\in U_p,x^2\equiv a\pmod p \\-1& \text{otherwise}\end{cases}
\]

勒让德符号的性质

欧拉准则

\[\left(\dfrac ap\right)\equiv a^{\frac{p-1}{2}}\pmod p
\]

证明：如果存在 \(x^2\equiv a\pmod p\)，那么 \(a^{\frac{p-1}{2}}\equiv x^{p-1}\equiv 1\pmod p\)。我们知道 \(a^{\frac{p-1}{2}}\equiv 1\pmod p\) 这个方程在 \(\bmod p\) 意义下只有 \(\dfrac{p-1}{2}\) 个根，刚好就是所有的 \(x^2\pmod p\)。

QED。

通过欧拉准则，在 OI 中可以使用 \(\mathcal O(\log p)\) 的算法来解勒让德符号，但是欧拉准则使用情况在 MO 中并不是太理想。

【例题】求解 \(\left(\dfrac{-1}{p}\right)\)。

解答：\(\left(\dfrac{-1}{p}\right)\equiv(-1)^{(p-1)/2}\)。所以如果 \(p\equiv 1\pmod 4\) 那么 \(-1\) 是二次剩余，如果 \(p\equiv3\pmod 4\) 那么不是。

【例题】证明 \(4n+1\) 型质数是无穷的。

解答：反之，记为 \(p_1,p_2,\dots,p_n\)。取 \(m=(2p_1p_2\dots p_n)^2+1\)，取 \(m\) 任意质因子 \(p\)。

由于 \(p|m\)，得到 \(-1\equiv (2p_1p_2\dots p_n)^2\pmod p\)，也就是 \(-1\) 为 \(\bmod p\) 意义下的二次剩余，得到 \(p\equiv1\pmod 4\)。然而 \(p\not\in\{p_1,p_2,\dots,p_n\}\)，矛盾！

---

在进入高斯引理之前先引入几个记号：

定义 \(P_p=\{1,2,\dots,\dfrac{p-1}{2}\}\)，\(N_p=\{-1,-2,\dots,-\dfrac{p-1}{2}\}\)。定义集合的数乘，据此定义得到 \(N_p=(-1)P_p\)。

高斯引理

假设 \(p\) 为奇质数，\(a\in U_p\)，则：

\[\left(\dfrac ap\right)=(-1)^\mu,\mu=|aP\cap N|
\]

证明：假设 \(x\not = y\in P\)，得到 \(xa\not\equiv±ya\pmod p\)，进而：\(aP\) 可以表示成二元集合 \(\{±1\},\{±2\},\dots,\{±\dfrac{p-1}{2}\}\)，每个集合选一个元素的集合。

形式化的，\(aP=\{\epsilon_ii|i\in P,\epsilon_i\in\{-1,1\}\}\)。

考虑算两次 \(\prod_{i\in aP}i\)。

第一次：\(\prod_{i\in aP}i=\prod_{i\in P}ai=a^{\frac{p-1}{2}}\left(\dfrac{p-1}{2}\right)!\)。

第二次：\(\prod_{i\in aP}i=\prod\epsilon_i\times\left(\dfrac{p-1}{2}\right)\)。

得到 \(\prod \epsilon_i\equiv a^{\frac{p-1}{2}}\pmod p\)。

显然 \(\prod \epsilon_i\) 是 \(1\) 还是 \(-1\) 取决于其中 \(-1\) 的数量，也就是 \(\mu\) 的奇偶性。

QED。

通过欧拉准则，我们可以简单的手膜 \(a\) 比较小的二次剩余。

【例题】证明 \(\left(\dfrac 2p\right)=(-1)^{\frac{p^2-1}{8}}\)。也就是 \(2\) 是 \(\bmod p\) 的二次剩余当且仅当 \(p\equiv ±1\pmod 4\)。

把 \(aP\) 算一下就可以了。

---

二次互反律

假设 \(p,q\) 为不同的奇质数，则：

\[\left(\dfrac pq\right)\left(\dfrac qp\right)=(-1)^{\frac{(p-1)(q-1)}{4}}
\]

证明：

根据高斯引理，\(|pP_q\cap N_q|\) 意义就是满足下述条件的 \(x\) 的数量：\(x\in P_q,px\in N_q\)。

即 \(0<x<\dfrac q2\) 且存在整数 \(y\) 使得 \(-\dfrac q2<px-qy<0\)。这里一个 \(x\) 只会对应一个 \(y\)，也就是对 \(x\) 计数等价于给合法的 \((x,y)\) 对计数。

根据不等式右边容易推出 \(y>0\)，根据左边得到 \(qy<px+\dfrac q2<\dfrac{pq}2+\dfrac q2\)，也就是 \(y<\dfrac{p+1}{2}\)。

也就是我们要对 \(0<x<\dfrac q2,0<y<\dfrac p2\)，且 \(-\dfrac q2<px-qy<0\) 的 \((x,y)\) 对计数。

我们考虑对 \(\left(\dfrac qp\right)\) 使用同样的操作，同样的化简可以得到是等价于：

• 对 \(0<x<\dfrac q2,0<y<\dfrac p2\)，且 \(0<px-qy<\dfrac p2\) 的 \((x,y)\) 对计数。

由于我们计算的是上面两个东西的即，我们只需要把满足这两个情况之一的 \((x,y)\) 对计数即可。

注意到 \(px-qy\not=0\)，也就是可以换成 \(-\dfrac q2<px-qy<\dfrac p2\)。搬一张图大概长这样：

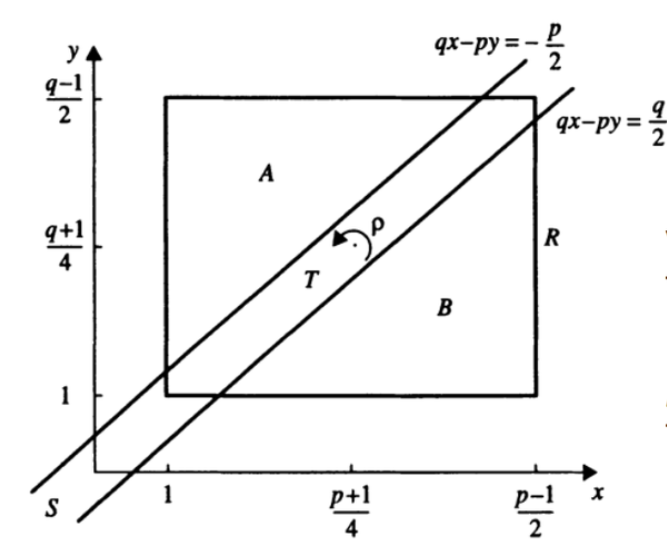
其中 \(A,B\) 部分是不满足的，中间长条部分是满足的。

经过计算不难发现 \(A,B\) 是全等的，也就是满足条件的 \((x,y)\) 对的奇偶性等价于这个矩形内部的整点个数 \(\dfrac{p-1}{2}\dfrac{q-1}{2}\)。

QED。

这种方式，我们可以解决 \(\left(\dfrac 3p\right)\) 之类的问题。