Tarjan算法求割点

(声明：以下图片来源于网络)

Tarjan算法求出割点个数

首先来了解什么是连通图

在图论中，连通图基于连通的概念。在一个无向图 G 中，若从顶点i到顶点j有路径相连（当然从j到i也一定有路径），则称i和j是连通的。如果 G 是有向图，那么连接i和j的路径中所有的边都必须同向。如果图中任意两点都是连通的，那么图被称作连通图。如果此图是有向图，则称为强连通图（注意：需要双向都有路径）。图的连通性是图的基本性质。

——摘自度娘

通俗易懂，不在解释。

举个例子吧：



如上图，各个节点皆可以到达任意节点，所以该图为连通图。

再来了解什么是割点

在一个无向图中，如果有一个顶点集合，删除这个顶点集合以及这个集合中所有顶点相关联的边以后，图的连通分量增多，就称这个点集为割点集合。

如果某个割点集合只含有一个顶点X（也即{X}是一个割点集合），那么X称为一个割点。

——摘自度娘

了解完定义之后，不难通过定义来求出图的割点——暴力DFS。

即是：从1到n遍历每一个点，每次遍历到这个点时，只需要删除该点，判断删除后是否会增加联通量即可。

这种方法时间复杂度最坏为\(O(n×(n+m))\)，只要数据大一点就会被卡爆，这里不详细叙述。

使用Tarjan算法求割点

可以参考本人的Tarjan算法缩点博客

依然定义：dfn（时间戳），low（该集合中最早遍历到的点的时间戳）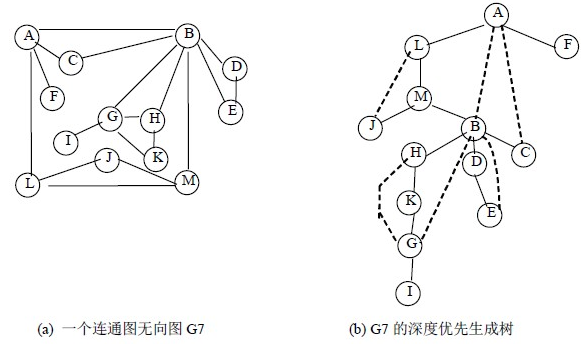

观察上图，可以发现割点求法可以分成两种情况讨论。

1. 若该点为根节点，若有该节点拥有两个及以上互不相连的子树，则删除该点会得到这些子树。所以该点为割点。
   
   （now == root && child >= 2）
2. 若该点不为根节点，若不存在可以在DFS中可以遇到已访问节点的连边时（通俗的说，就是不可以找到回去的路），则该点为割点。
   
   （now != root && low[next] >= dfn[now]）

low的值可以证明发现：

low的初始值为该节点的时间戳。

即是：low[now]=dfn[now]。

若当前结点 now 的所连结点 next 正在被访问，则 low[now]=min(low[now],dfn[next]) 。

若当前结点 now 的所连结点 next 未被访问，则

low[now]=min(low[now],low[next])。

C++代码实现：

void Tarjan(int now, int father, int root) {
	dfn[now] = low[now] = ++tim;
	int child = 0; //若now为根节点时子树的个数
	int SIZ = v[now].size();
	for(int i = 0; i < SIZ; i++) {
		int next = v[now][i];
		if(!dfn[next]) {
			if(now == root) {
				child++;
			}
			Tarjan(next, now, root);
			low[now] = min(low[now], low[next]);
			if(now == root && child >= 2)//处理情况一
				cut[now] = true;
			else if(now != root && low[next] >= dfn[now])//处理情况二
				cut[now] = true;
		}
		if(next != father)
			low[now] = min(low[now], dfn[next]);//更新low值
	}
}
void Build() {
	for(int i = 1; i <= n; i++)
		if(!dfn[i])
			Tarjan(i, i, i);
}

附上一道板题

题目背景

割点

题目描述

给出一个\(n\)个点，\(m\)条边的无向图，求图的割点。

输入格式

第一行输入两个正整数\(n,m\)。

下面\(m\)行每行输入两个正整数\(x,y\)表示\(x\)到\(y\)有一条边。

输出格式

第一行输出割点个数。

第二行按照节点编号从小到大输出节点，用空格隔开。

输入输出样例

输入

6 7
1 2
1 3
1 4
2 5
3 5
4 5
5 6

输出

1
5

思路

板题，套上即可。

C++代码：

#include <cstdio>
#include <vector>
using namespace std;
const int MAXN = 2e4 + 5;
vector<int> v[MAXN];
int dfn[MAXN], low[MAXN];
bool cut[MAXN];
int tim, cnt;
int n, m;
void Read();
void Build();
void Tarjan(int, int, int);
int main() {
	Read();
	Build();
	return 0;
}
void Build() {
	for(int i = 1; i <= n; i++)
		if(!dfn[i])
			Tarjan(i, i, i);
	for(int i = 1; i <= n; i++)
		if(cut[i])
			cnt++;
	printf("%d\n", cnt);
	for(int i = 1; i <= n; i++)
		if(cut[i])
			printf("%d ", i);
}
void Tarjan(int now, int father, int root) {
	dfn[now] = low[now] = ++tim;
	int child = 0;
	int SIZ = v[now].size();
	for(int i = 0; i < SIZ; i++) {
		int next = v[now][i];
		if(!dfn[next]) {
			if(now == root) {
				child++;
			}
			Tarjan(next, now, root);
			low[now] = min(low[now], low[next]);
			if(now == root && child >= 2)
				cut[now] = true;
			else if(now != root && low[next] >= dfn[now])
				cut[now] = true;
		}
		if(next != father)
			low[now] = min(low[now], dfn[next]);
	}
}
void Read() {
	scanf("%d %d", &n, &m);
	for(int i = 1; i <= m; i++) {
		int A, B;
		scanf("%d %d", &A, &B);
		v[A].push_back(B);
		v[B].push_back(A);
	}
}