2018ICPC南京 A. Adrien and Austin

题目：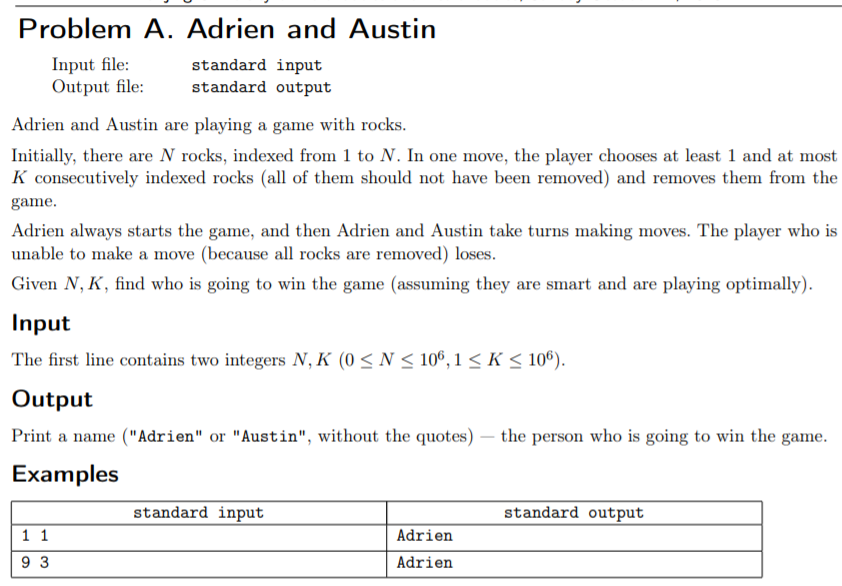

题意：1-N个石子每次只能取连续的1-K个问输赢。（一开始以为只是个简简单单的巴什游戏，激动的提交了一发wr了，再读了一遍题才发现是只能取连续的）

题解：当n==0或者k==1&&n&1==1 后手才会赢，其他情况都是先手赢。

1 #include<bits/stdc++.h>
2 using namespace std;
3 int main()
4 {
5     int n,k;scanf("%d%d",&n,&k);
6     if(n==0||(k==1&&!(n&1))) puts("Austin");
7     else puts("Adrien");
8 }