HYSBZ 1734 二分

传送门

题面：

农夫 John 建造了一座很长的畜栏，它包括N (2 <= N <= 100,000)个隔间，这些小隔间依次编号为x1,...,xN (0 <= xi <= 1,000,000,000). 但是，John的C (2 <= C <= N)头牛们并不喜欢这种布局，而且几头牛放在一个隔间里，他们就要发生争斗。为了不让牛互相伤害。John决定自己给牛分配隔间，使任意两头牛之间的最小距离尽可能的大，那么，这个最大的最小距离是什么呢 ？

Input

* Line 1: Two space-separated integers: N and C * Lines 2..N+1: Line i+1 contains an integer stall location, xi

第一行：空格分隔的两个整数N和C

第二行---第N+1行：i+1行指出了xi的位置

Output

* Line 1: One integer: the largest minimum distance

第一行：一个整数，最大的最小值

Sample Input

5 3

1

2

8

4

9

题面描述

给出小隔间的编号（位置），然后把牛按一定的方法放进小隔间，要求任意两头牛之间的距离中，最小的那个距离相比于其他把牛放进隔间的方法的最小距离比较，是最大的。

题目分析

这里难就难在理解题意，就拿题目中的样例来说吧：有5个隔间，三头牛，给出了5个隔间的位置，就是：

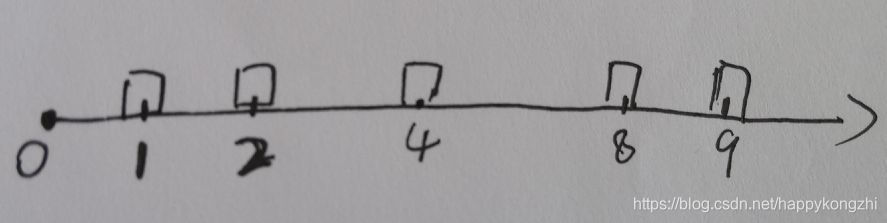
现在要把三头牛放到这些隔间里面，怎样放才能是符合题意的答案呢？首先我们可以尝试把牛放到1，2，4号隔间，这时任意两头牛的最小距离是1，即任意选两头牛，它们的距离肯定是大于等于1的，这个1就称为任意两头牛的最小距离。我们尝试第二种方法：把牛放到2，4，8号隔间，这时任意两头牛的最小距离是2，2比刚刚的最小距离为1要大，所以舍弃1这个答案。我们再想一想，还有没有比2还要大的摆法？当然有(这不是废话嘛，题目都说答案是3了 )。我们可以尝试把牛放进1，4，8号隔间，这时最小距离是不是3？这个距离3比2和1都要大，而且我们也找不到最小距离比3还要大的摆法了，所以，这个最大的任意两头牛之间的最小距离为3。

那么，现在理解题意之后，有人会问，这跟二分有什么关系？这道题如何运用二分的思想？我们再看回题目：题目中告诉了我们两个隔间最小距离为1，最大距离为1,000,000,000。如果我们从大到小去一个一个验证是否可行，那肯定会超时，所以我们要用到二分的思想来减少运算时间。现在问题转化为如何用二分去解决这道题。我们回顾一下二分的主要代码：

    while(r > l){
        guess = (r+l)/2;
        if(guess < res) l = guess+1;
        else r = guess;
    }

其中：guess < res是我们更新依据，如果猜的数比结果小，更新左端点，否则更新右端点。这道题也是类似，重点就在这个判断依据上面。假如我们已经写了一个交check()的函数，这个函数可以验证你猜的距离guess是否成立(也就是按照你的最小距离放置，奶牛是可以全部放进隔间的)，如果成立，就说明答案肯定是大于等于guess的，为什么呢？因为如果答案小于guess，而我当距离为guess时也成立，那么这个最大距离就不是答案，而是guess。所以凡是小于guess的距离都不用去考虑。即:

if(check(guess)) l = guess;

如果guess这个距离不成立的话，那么答案肯定比guess小，因为以guess为最小距离都不能把所有的牛放到隔间，更大的距离当然更加不行。所以拼凑起来就是：

if(check(guess)) l = guess;
else r = guess-1;

很显然，这是个左闭右开的区间，所以记得guess要向上取整。

最后把check()函数搞定就行了。AC代码：

#include <iostream>
#include <algorithm>
using namespace std;
const int maxn = 1e6 + 5;
long long a[maxn];
int n, c;

bool check(int m){
    int cnt = c;
    cnt--;
    int t = 0;
    for(int i = 1; i < n; i++){
        if(a[i]-a[t] >= m){
            cnt--;
            t = i;
        }
    }
    return cnt <= 0;
}

int main(){
    cin >> n >> c;
    for(int i = 0; i < n; i++) cin >> a[i];
    sort(a, a+n);
    int l, r;
    l = 1;
    r = 1e9;
    int guess;
    while(r > l){
        guess = (l+r+1)/2;
        if(check(guess)) l = guess;
        else r = guess-1;
    }
    cout << l << endl;
    return 0;
}