Network of Schools POJ - 1236 有向强连通图

//题意：
//给你n个学校，其中每一个学校都和一些其他学校有交流，但是这些边都是单向的。你至少需要给几个学校
//传递消息可以使全部学校都收到消息，第二问你最少添加几条边可以使它变成一个强连通图
//题解：
//首先是第一问，这个你只需要找出来一共有几个连通块就可以了，也相当于有几个入度为0的点（这个时候就不是
//之前的图，是要缩点后的图来找出入度）
//第二问：找出来所有点中max(入度为0，出度为0)

为什么要找它们的最大值：（黑边为原来存在的，红边是添加的，使这个图变成强连通图的）

或者

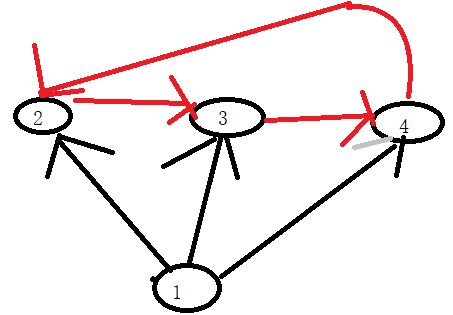
反正不管怎么连边，它们对少需要3条边才可以成为强连通图（从任意一个点可以到达图中的其他点）

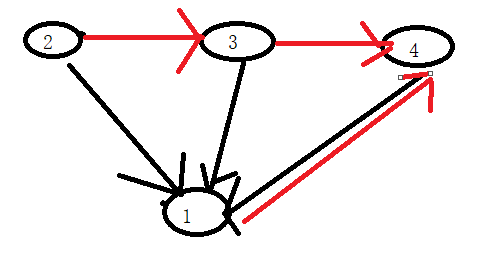
或者

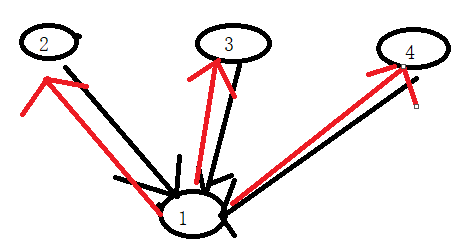
上代码：

  1 //题意：
  2 //给你n个学校，其中每一个学校都和一些其他学校有交流，但是这些边都是单向的。你至少需要给几个学校
  3 //传递消息可以使全部学校都收到消息，第二问你最少添加几条边可以使它变成一个强连通图
  4 //题解：
  5 //首先是第一问，这个你只需要找出来一共有几个连通块就可以了，也相当于有几个入度为0的点（这个时候就不是
  6 //之前的图，是要缩点后的图来找出入度）
  7 //第二问：找出来所有点中max(入度为0，出度为0)
  8 #include<stdio.h>
  9 #include<string.h>
 10 #include<iostream>
 11 #include<algorithm>
 12 #include<map>
 13 #include<math.h>
 14 #include<set>
 15 #include<queue>
 16 using namespace std;
 17 typedef long long ll;
 18 const int maxn=105;
 19 const int mod=26;
 20 const int INF=0x3f3f3f3f;
 21 const int block=300;
 22 struct edge
 23 {
 24     int u,v,next;
 25     bool sign;
 26 }e[maxn*maxn];
 27 int head[maxn],cnt;
 28 void add_edge(int x,int y)
 29 {
 30     e[cnt].u=x;
 31     e[cnt].v=y;
 32     e[cnt].next=head[x];
 33     head[x]=cnt++;
 34 }
 35 int dfn[maxn],low[maxn],stacks[maxn],top,tot;
 36 int taj;
 37 int belong[maxn],visit[maxn];
 38 vector<int>w[maxn];
 39 void tarjan(int x,int fx)
 40 {
 41     dfn[x]=low[x]=++tot;
 42     stacks[top++]=x;
 43     visit[x]=1;
 44     for(int i=head[x];i!=-1;i=e[i].next)
 45     {
 46         int v=e[i].v;
 47         if(!dfn[v])
 48         {
 49             tarjan(v,x);
 50             low[x]=min(low[x],low[v]);
 51             if(dfn[x]<low[v])
 52             {
 53                 e[i].sign=1;
 54             }
 55         }
 56         else if(visit[v])
 57         {
 58             low[x]=min(low[x],dfn[v]);
 59         }
 60     }
 61     if(low[x]==dfn[x])
 62     {
 63         int now;
 64         taj++;
 65         w[taj].clear();
 66         do{
 67             now=stacks[--top];
 68             visit[now]=0;
 69             belong[now]=taj;
 70             w[taj].push_back(now);
 71         }while(now!=x);
 72     }
 73 }
 74 void tarjan_init(int n)
 75 {
 76     memset(visit,0,sizeof(visit));
 77     top=tot=taj=0;
 78     for(int i=1;i<=n;++i)
 79     {
 80         if(!dfn[i]) tarjan(i,i);
 81     }
 82 }
 83 vector<int>g[maxn];
 84 int cu[maxn],ru[maxn];
 85 void suodian()
 86 {
 87     memset(cu,0,sizeof(cu));
 88     memset(ru,0,sizeof(ru));
 89     for(int i=1;i<=taj;++i)
 90         g[i].clear();
 91     for(int i=0;i<cnt;++i)
 92     {
 93         int u=belong[e[i].u];
 94         int v=belong[e[i].v];
 95         if(u!=v) g[u].push_back(v),cu[u]++,ru[v]++;//printf("%d %d\n",u,v);
 96     }
 97 }
 98 int vis[maxn];
 99 void init()
100 {
101     memset(head,-1,sizeof(head));
102     cnt=0;
103 }
104 int main()
105 {
106     int a,n;
107     scanf("%d",&n);
108     init();
109     for(int i=1;i<=n;++i)
110     {
111         while(~scanf("%d",&a) && a)
112         {
113             add_edge(i,a);
114         }
115     }
116     tarjan_init(n);
117     if(taj==1)
118     {
119         printf("1\n0\n");
120         return 0;
121     }
122 //    for(int i=1;i<=n;i++)
123 //
124 //    if(dfn[i]==-1)
125 //
126 //    tarjan(i,-1);
127     //for(int i)
128     //printf("%d**\n",taj);
129     suodian();
130     int ans1=0,ans2=0;
131     for(int i=1;i<=taj;++i)
132     {
133         if(ru[i]==0)
134             ans1++;
135         if(cu[i]==0)
136             ans2++;
137     }
138     printf("%d\n%d\n",ans1,max(ans1,ans2));
139     return 0;
140 }