「CSP-S 2019」划分

description

loj 3212

solution

首先容易想到\(n^3\)DP,即令\(f_{i,j}\)表示前\(i\)个数的划分，其中最后一段是从\(j\)开始时的答案

于是有

\[f_{i,j}=max(f_{j-1,k}+(s_i-s_{j-1})^2)
\]

其中\(s_i\)是前缀和，且\(k<j，s_i-s_{j-1} \ge s_{j-1}-s{k}\)

考虑优化，可以发现对于同一个\(i\)的\(j_1<j_2\)，不满足\(j_1\)条件的\(k\)也不会满足\(j_2\)的条件，所有当\(j\)增加时，对应的\(k\)也会单调递增，所以就可以\(O(n^2)\)做了

通过仔细观察(?)/打表，你会发现总存在\(f_{i,j} \ge f_{i,j-1}\)(在\(j\)与\(j-1\)均合法的情况下)，于是我们可以得到一个结论——在合法的情况下，让最后一段尽量小一定更优

那么怎么证明呢？

考虑最后两段的的情况如图所示：



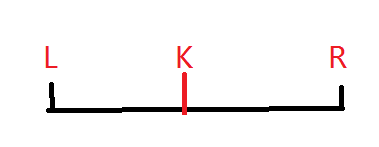
此时，后2段的答案就是\(A=(s_{K-1}-s_{L-1})^2+(s_R-s_{K-1})^2\)（图中的2段为\([L,K-1]\)与\([K,R]\)）

如果将最后一段长度变小，将原来的2段变为\([L,K]与[K+1,R]\)（满足此时依然合法）

则答案变为\(B=(s_K-s_{L-1})^2+(s_R]-s_K)^2\)

由于

\[A=s_R^2+2*s_{K-1}^2+s_{L-1}^2-2*s_{K-1}*(s_{L-1}+s_R)
\]

\[B=s[R]^2+2*s[K]^2+s[L-1]^2-2*s[K]*(s[L-1]+s[R])
\]

于是

\[B-A=2*(s[K]^2-s[K-1]^2-(s[L-1]+s[R])*(s[K]-s[K-1]))
\]

\[=2*(s[K]-s[K-1])*(s[K]+s[K-1]-s[L-1]-s[R])
\]

因为当前情况下合法，故

\[s[R]-s[K] \ge s[K]-s[L-1
\]

于是

\[s[R]+s[L-1] \ge 2*s[K] \ge s[K]+s[K-1]
\]

于是\(B-A<0\)，故\(B<A\)，后者比前者更优，得证

那么就可以上单调队列，维护最后一段的长度单调递增的一些数，因为前缀和单调递增，所以可以在\(l+1\)满足条件时将\(l\)弹掉，时间复杂度\(O(n)\)

懒得写高精，直接上__int128。

code

#include<bits/stdc++.h>
using namespace std;
const int N=4e7+10;
const int M=1e5+10;
typedef long long ll;
const ll mod=1<<30;
int n,type,q[N],l=1,r,p[M],L[M],R[M],x,y,z,m,pre[N];
ll s[N],b[N];
__int128 ans;
void write(__int128 x){
	if(x>9) write(x/10);
	putchar(x%10+'0');
}
inline int read(){
	int x=0,f=1;char ch=getchar();
	while(!isdigit(ch)){if(ch=='-') f=-1;ch=getchar();}
	while(isdigit(ch)){x=(x<<3)+(x<<1)+(ch^48);ch=getchar();}
	return x*f;
}
int main(){
    freopen("partition.in","r",stdin);
    freopen("partition.out","w",stdout);
	n=read();type=read();
	if(type==1){
		x=read(),y=read(),z=read();b[1]=read();b[2]=read();m=read();
		for(int i=1;i<=m;i++) p[i]=read(),L[i]=read(),R[i]=read();
		for(int i=3;i<=n;i++)b[i]=(x*b[i-1]+y*b[i-2]+z)%mod;
		int j=1;
        for(int i=1;i<=n;i++){
			if(i>p[j]) ++j;
			s[i]=s[i-1]+(b[i]%(R[j]-L[j]+1))+L[j];
		}
	}
	else for(int i=1;i<=n;++i) s[i]=read()+s[i-1];
	for(int i=1;i<=n;++i){
		while(l<=r&&s[q[l]]-s[pre[q[l]]]<=s[i]-s[q[l]]) ++l;
		--l;pre[i]=q[l];
		while(l<=r&&s[q[r]]-s[pre[q[r]]]+s[q[r]]>=s[i]-s[pre[i]]+s[i]) --r;
		q[++r]=i;
	}
	int now=n;while(now) ans+=((__int128)s[now]-s[pre[now]])*(s[now]-s[pre[now]]),now=pre[now];
	write(ans);
	return 0;
}