论文解读（IGSD）《Iterative Graph Self-Distillation》

论文信息

论文标题：Iterative Graph Self-Distillation
论文作者：Hanlin Zhang, Shuai Lin, Weiyang Liu, Pan Zhou, Jian Tang, Xiaodan Liang, Eric P. Xing
论文来源：2021, ICLR
论文地址：download 
论文代码：download

1 Introduction

　　创新点：图级对比。

2 Method

　　整体框架如下：

　　

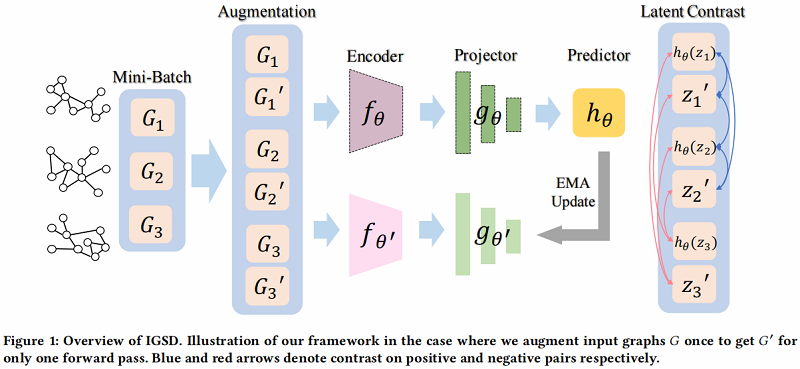
2.1 Iterative Graph Self-Distillation Framework

　　在 IGSD 中，引入了一个结构相似的两个网络，由 encoder $f_{\theta}$、projector  $g_{\theta}$  和 predictor  $h_{\theta}$ 组成。我们将教师网络和学生网络的组成部分分别表示为 $f_{\theta^{\prime}}$、$g_{\theta^{\prime}}$  和 $f_{\theta}$、$g_{\theta}$、$h_{\theta}$

　　IGSD 过程描述如下：

• • 首先对原始输入图 $G_{j}$ 进行扩充，以获得增广视图 $G_{j}^{\prime}$。然后将 $G_{j}^{\prime}$ 和不同的图实例 $G_{i}$ 分别输入到两个编码器 $f_{\theta}$、$f_{\theta^{\prime}}$ 中，用于提取图表示 $\boldsymbol{h}, \boldsymbol{h}^{\prime}=f_{\theta}\left(G_{i}\right), f_{\theta^{\prime}}\left(G_{j}^{\prime}\right) $；
  • 其次，投影头 $g_{\theta}$，$g_{\theta^{\prime}}$ 通过 $z=g_{\theta}(\boldsymbol{h})=W^{(2)} \sigma\left(W^{(1)} \boldsymbol{h}\right)$ 和 $z^{\prime}=g_{\theta^{\prime}}\left(\boldsymbol{h}^{\prime}\right)=W^{\prime(2)} \sigma\left(W^{\prime(1)} \boldsymbol{h}^{\prime}\right) $  转换图表示 $\boldsymbol{h}, \boldsymbol{h}^{\prime}$ 到投影 $z$，$z^{\prime}$，其中 $\sigma$ 表示ReLU非线性；
  • 最后，为防止崩溃为一个平凡的解，在学生网络中使用预测头来获得投影 $z$ 的预测 $h_{\theta}(z)=W_{h}^{(2)} \sigma\left(W_{h}^{(1)} z\right) $；

　　通过对称传递两个图实列 $G_{i}$ 和 $G_{j}$，可以得到总体一致性损失：

　　　　$\mathcal{L}^{\text {con }}\left(G_{i}, G_{j}\right)=\left\|h_{\theta}\left(z_{i}\right)-z_{j}^{\prime}\right\|_{2}^{2}+\left\|h_{\theta}\left(z_{i}^{\prime}\right)-z_{j}\right\|_{2}^{2}\quad\quad\quad(2)$

　　在一致性损失的情况下，teacher network 提供了一个回归目标来训练 student network，在通过梯度下降更新 student network 的权值后，将其参数 $\theta^{\prime}$ 更新为学生参数 $\theta$  的指数移动平均值(EMA)：

　　　　$\theta_{t}^{\prime} \leftarrow \tau \theta_{t-1}^{\prime}+(1-\tau) \theta_{t}\quad\quad\quad(3)$

2.2 Self-supervised Learning with IGSD

　　给定一组无标记图 $\mathcal{G}=\left\{G_{i}\right\}_{i=1}^{N}$，我们的目标是学习每个图 $G_{i} \in \mathcal{G}$ 的低维表示，有利于下游任务，如图分类。

　　在 IGSD 中，为了对比锚定 $G_{i}$ 与其他图实例$G_{j}$（即负样本），使用以下自监督的 InfoNCE 目标：

　　　　${\large \mathcal{L}^{\text {self-sup }}=-\mathbb{E}_{G_{i} \sim \mathcal{G}}\left[\log \frac{\exp \left(-\mathcal{L}_{i, i}^{\mathrm{con}}\right)}{\exp \left(-\mathcal{L}_{i, i}^{\mathrm{con}}\right)+\sum_{j=1}^{N-1} \mathbb{I}_{i \neq j} \cdot \exp \left(-\mathcal{L}_{i, j}^{\mathrm{con}}\right)}\right]} $

　　其中，$\mathcal{L}_{i, j}^{\text {con }}=\mathcal{L}^{\text {con }}\left(G_{i}, G_{j}\right)$ 。

　　我们通过用混合函数 $\operatorname{Mix}_{\lambda}(a, b)=\lambda \cdot a+(1-\lambda) \cdot b$：融合潜在表示 $\boldsymbol{h}=f_{\theta}(G) $ 和 $\boldsymbol{h}^{\prime}=f_{\theta^{\prime}}(G)$，得到图表示 $\tilde{\boldsymbol{h}}$ ：

　　　　$\tilde{\boldsymbol{h}}=\operatorname{Mix}_{\lambda}\left(\boldsymbol{h}, \boldsymbol{h}^{\prime}\right)$

2.3 Semi-supervised Learning with IGSD

　　考虑一个整个数据集 $\mathcal{G}=\mathcal{G}_{L} \cup \mathcal{G}_{U}$ 由标记数据 $\mathcal{G}_{L}=   \left\{\left(G_{i}, y_{i}\right)\right\}_{i=1}^{l}$ 和未标记数据 $G_{U}=\left\{G_{i}\right\}_{i=l+1}^{l+u} $（通常 $u \gg l$ ），我们的目标是学习一个模型，可以对不可见图的图标签进行预测。生成 $K$ 个增强视图，我们得到了 $ \mathcal{G}_{L}^{\prime}=   \left\{\left(G_{k}^{\prime}, y_{k}^{\prime}\right)\right\}_{k=1}^{K l} $ 和 $\mathcal{G}_{U}^{\prime}=\left\{G_{k}^{\prime}\right\}_{k=l+1}^{K(l+u)} $ 作为我们的训练数据。

　　为了弥合自监督的预训练和下游任务之间的差距，我们将我们的模型扩展到半监督设置。在这种情况下，可以直接插入自监督损失作为表示学习的正则化器。然而，局限于标准监督学习的实例性监督可能会导致有偏的负抽样问题。为解决这一问题，我们可以使用少量的标记数据来进一步推广相似性损失，以处理属于同一类的任意数量的正样本：

　　　　$\mathcal{L}^{\text {supcon }}=\sum\limits_{i=1}^{K l} \frac{1}{K N_{y_{i}^{\prime}}} \sum\limits_{j=1}^{K l} \mathbb{I}_{i \neq j} \cdot \mathbb{I}_{y_{i}^{\prime}=y_{j}^{\prime}} \cdot \mathcal{L}^{\text {con }}\left(G_{i}, G_{j}\right)\quad\quad\quad(5)$

　　其中，$N_{y_{i}^{\prime}}$ 表示训练集中与锚点 $i$ 具有相同标签 $y_{i}^{\prime}$ 的样本总数。由于IGSD的图级对比性质，我们能够缓解带有监督对比损失的有偏负抽样问题，这是至关重要的，但在大多数 context-instance 对比学习模型中无法实现，因为子图通常很难给其分配标签。此外，有了这种损失，我们就能够使用自我训练来有效地调整我们的模型，其中伪标签被迭代地分配给未标记的数据。

　　对于交叉熵或均方误差 $\mathcal{L}\left(\mathcal{G}_{L}, \theta\right) $，总体目标可以总结为：

　　　　$\mathcal{L}^{\text {semi }}=\mathcal{L}\left(G_{L}, \theta\right)+w \mathcal{L}^{\text {self-sup }}\left(\mathcal{G}_{L} \cup \mathcal{G}_{U}, \theta\right)+w^{\prime} \mathcal{L}^{\text {supcon }}\left(\mathcal{G}_{L}, \theta\right)\quad\quad\quad(6)$

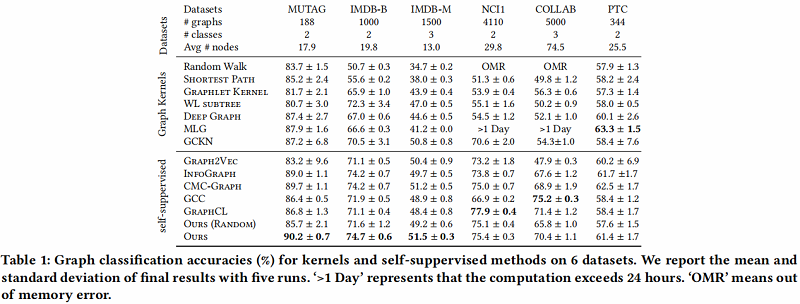
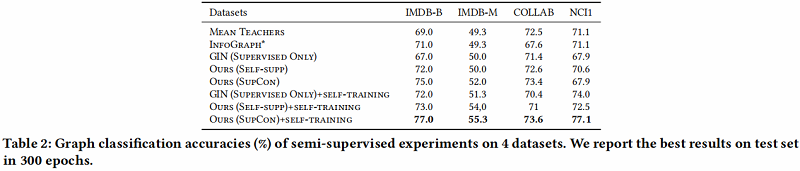
3 Experiments

节点分类

　　

　　

3 Conclusions

　　在本文中，我们提出了一种新的基于自蒸馏的图级表示学习框架IGSD。我们的框架通过对图实例的增强视图的实例识别，迭代地执行师生精馏。在自监督和半监督设置下的实验结果表明，IGSD不仅能够学习与最先进的模型竞争的表达性图表示，而且对不同的编码器和增强策略的选择也有效。在未来，我们计划将我们的框架应用到其他的图形学习任务中，并研究视图生成器的设计，以自动生成有效的视图。